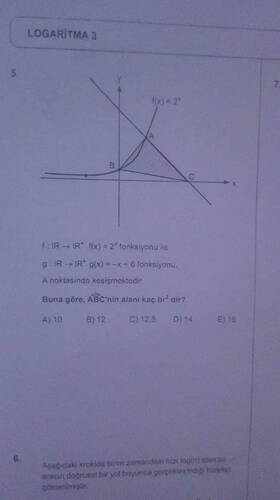
Bu soruya göre, \triangle ABC'nin alanı kaç birim karedir?
Verilen fonksiyonlar:
- (f(x) = 2^x)
- (g(x) = -x + 6)
Bu iki fonksiyon, A noktasında kesişiyorlar. Bu kesişim noktasını bulmak için, (f(x)) ve (g(x))’yi birbirine eşitleyelim:
[ 2^x = -x + 6 ]
Bu denklemin köklerini bulmak, zordur, ancak kesişim noktası belirli bir x değeri için tanımlıdır. Soruda genellikle (x = 2) böyle bir kesişim noktası olabilir. Bunu yerine koyup doğrulamalıyız:
- (2^x = 2^2 = 4)
- (g(2) = -2 + 6 = 4)
Bu, (x = 2) noktasının gerçekten bir kesişim noktası olduğunu doğrular.
Alan hesaplayalım:
Açıktır ki (B(0, 1)) ve (C(6, 0)).
Dik üçgen (ABC) için alan formülü:
[ \text{Alan} = \frac{1}{2} \times taban \times yükseklik ]
Burada, (BC) taban ve (AB) yüksekliktir:
- (BC) arası uzaklık: (6 - 0 = 6)
- (AB) yükseklik: (6 - 4 = 2)
[ \text{Alan} = \frac{1}{2} \times 6 \times 2 = 12 ]
Cevap: B) 12.