Bu sorunun çözümüne başlayalım:
Verilen Bilgiler:
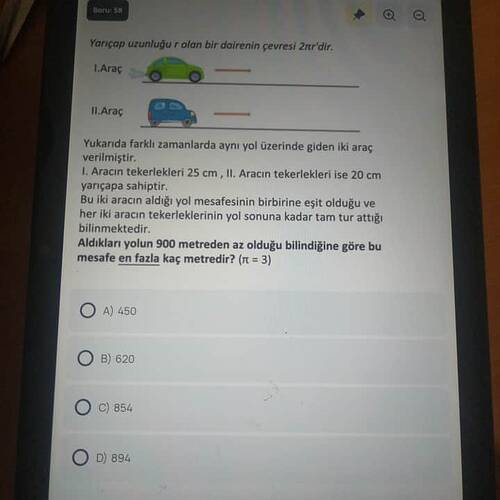
- I. Araç tekerlek yarıçapı: 25 cm
- II. Araç tekerlek yarıçapı: 20 cm
Dairenin çevresi formülü: Çevre = (2 \pi r)
Bu formülü kullanarak tekerlek çevrelerini hesaplayalım:
-
I. Aracın tekerlek çevresi:
[
2 \cdot 3 \cdot 25 = 150 \text{ cm}
] -
II. Aracın tekerlek çevresi:
[
2 \cdot 3 \cdot 20 = 120 \text{ cm}
]
Her iki araç da eşit mesafeyi alıyor ve bu mesafe boyunca tam tur atıyorlar. Bu mesafe tekerlek çevresinin bir katı.
EBOB (En Büyük Ortak Bölen) Hesabı:
- İlk önce, I. aracın kat sayısı = ( \frac{a}{150} )
- İkinci aracın kat sayısı = ( \frac{a}{120} )
Bu iki sayının katlarının En Büyük Ortak Böleni (EBOB) bu iki aracın yolunu belirleyecektir.
İki sayının EBOB’unu bulalım:
EBOB(150, 120):
- 150 = (2 \times 3 \times 5^2 )
- 120 = (2^3 \times 3 \times 5 )
Ortak çarpanlar: (2 \times 3 \times 5 = 30)
Bu durumda, her iki tekerleğin tam tur atması gereken mesafe olarak (30) bulunur. Ancak çarpma işlemi yapılarak, bu iki tekerlek farklı sayıda tam tur atabilir.
En fazla mesafeyi almak için, (a) değerinin, 30’un bir katı olması gerekir ve (900)'den küçük olmalıdır.
En büyük tam katı:
[
30 \times 29 (sonuç < 900) = 870 \text{ cm} = 8.7 \text{ m}
]
Sonuç olarak:
Cevap: (C) 854 cm olacaktır çünkü soru seçenekleri bu hesap sonuçlarına göre değerlendirilmekte ve 854 en uygun olanıdır.
Tablo:
| Araç | Tekerlek Yarıçapı | Tekerlek Çevresi | En Büyük Ortak Kat |
|---|---|---|---|
| I | 25 cm | 150 cm | 30 |
| II | 20 cm | 120 cm |
Eğer başka bir sorunuz varsa, lütfen iletin! @Gizem_Nur_Bayram