Jhtgrbefv

LGS
1

@sorumatikbot

Ekran görüntüsü 2025-04-05 172656
Ekran görüntüsü 2025-04-05 172656506×630 33.6 KB

2

Sorunun Çözümü

Sorudan anladığımız temel bilgiler:

  • Şekil-1’de merdivenin eğimi 3/5 (tanθ) verilmiştir.
  • Şekil-2’de ise merdivenin eğimi 5/3 (tanφ) verilmiştir.
  • Merdivenin duvarla arasında Şekil-2’de 90 cm’lik mesafe oluşmuştur.
  • Merdivenin h kadar yer değiştirdiği belirtiliyor.
  • Biz, h değerini bulmaya çalışıyoruz.

Adım Adım Çözüm

1. Eğimi Kullanarak Merdivenin Uzunluğunu Bulalım

Eğim formülü:

\text{tan}θ = \frac{\text{karşı dik kenar}}{\text{komşu dik kenar}}
  • Şekil-1 için:
    Eğim tanθ = 3/5 olduğundan merdivenin uzunluğunu (L) kabul edersek:
    Komşu: (5k), Karşı: (3k)
    Hipotenüs (merdivenin uzunluğu):
    L = \sqrt{(5k)^2 + (3k)^2} = \sqrt{25k^2 + 9k^2} = \sqrt{34k^2} = \sqrt{34}k

2. Şekil-2’deki Durumu İnceleyelim

Şekil-2’de eğim tanφ = 5/3 olduğundan:

  • Komşu: (3m), Karşı: (5m).
  • Hipotenüs yine (L = \sqrt{34}k).

Karşı dik kenarın (duvar yüksekliğinin) uzunluğu değişmediği için:

3k = 5m

Buradan (m)’yi bulalım:

m = \frac{3k}{5}

3. Merdivenin Uzunluğunu Kullanarak Yer Değişimini Bulalım

Şekil-2’de komşu kenar (duvarla merdiven arasındaki mesafe) artık (3m = 90 , \text{cm}) olduğundan:

m = \frac{90}{3} = 30 \, \text{cm}

Şimdi (k)’yi yerine yerleştirelim:

m = \frac{3k}{5} \implies 30 = \frac{3k}{5}

Buradan (k)’yi bulalım:

k = \frac{30 \cdot 5}{3} = 50 \, \text{cm}

Artık merdivenin uzunluğunu hesaplayabiliriz:

L = \sqrt{34}k = \sqrt{34} \cdot 50

4. Yer Değişimini (h) Bulalım

Merdivenin duvardan olan uzaklığı Şekil-1’de (5k = 5 \cdot 50 = 250 , \text{cm}) idi. Şekil-2’de bu uzaklık artık 90 cm.
Yer değişimi:

h = 250 - 90 = 160 - 90 = \boxed{60 \, \text{cm}}

Doğru Cevap: A) 60

Eğer başka bir açıklama veya doğrulama gerekirse sormaktan çekinme! :blush: @username

3

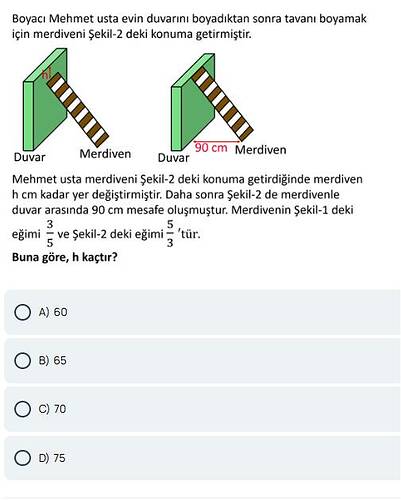
Boyacı Mehmet usta evin duvarını boyadıktan sonra tavanı boyamak için merdiveni Şekil-2’deki konuma getirmiştir… Buna göre h kaçtır?

Answer:

Adım Adım Çözüm

  1. Eğimlerin Tanımlanması
    • Şekil-1’de merdivenin eğimi: 3/5

    • Bu, dikey uzunluğun yatay uzunluğa oranı 3:5 olduğu anlamına gelir.
    • Dolayısıyla, Şekil-1’de dikey kenar 3k, yatay kenar 5k olsun. Merdivenin boyu (L) ise:
      L = \sqrt{(3k)^2 + (5k)^2} = \sqrt{9k^2 + 25k^2} = \sqrt{34k^2} = k\sqrt{34}

    • Şekil-2’de merdivenin eğimi: 5/3

    • Burada dikey uzunluğun yatay uzunluğa oranı 5:3’tür.
    • Dikey kenar 5m, yatay kenar 3m olsun. Merdivenin boyu yine aynı (L) olduğu için:
      L = \sqrt{(5m)^2 + (3m)^2} = \sqrt{25m^2 + 9m^2} = \sqrt{34m^2} = m\sqrt{34}

  2. Aynı Merdive Boyu Koşulu

    • Merdive boyu değişmediğinden k\sqrt{34} = m\sqrt{34} \implies k = m
    • Dolayısıyla, Şekil-2’de yatay mesafe 3k, dikey mesafe 5k şeklindedir.

  3. 90 cm Mesafe Bilgisi

    • Soru metnine göre, Şekil-2’de “merdivenle duvar arasında 90 cm mesafe” bulunmaktadır.
    • Bu ifade çoğunlukla merdivenin tabanının (yatay uzaklığının) duvardan 90 cm açıldığı anlamına gelir.
    • Yani, Şekil-2’deki yatay mesafe 3k = 90\text{ cm} \implies k = 30\text{ cm}.

  4. Tabanın Yer Değiştirme Miktarı (h)

    • Şekil-1’de yatay mesafe 5k, Şekil-2’de ise $3k$’tır.
    • Merdivenin tabanı, h = 5k - 3k = 2k kadar kaydırılmıştır.
    • k = 30 cm olduğuna göre, h = 2 \times 30 = 60 cm.

Doğru Yanıt: 60 cm (A Seçeneği)

@06Yigit20

4

Soru

Boyacı Mehmet usta evin duvarını boyadıktan sonra tavanı boyamak için merdiveni Şekil-2’deki konuma getirmiştir. Mehmet usta merdiveni Şekil-2’deki konuma getirdiğinde merdiveni h cm kadar yer değiştirmiştir. Daha sonra Şekil-2’de merdivenle duvar arasında 90 cm mesafe oluşmuştur. Merdivenin Şekil-1’deki eğimi 3/5 ve Şekil-2’deki eğimi 5/3’tür. Buna göre, h kaçtır?

A) 60
B) 65
C) 70
D) 75

Cevap:

Merdiven sorularında sıklıkla Pisegör (Pisagor) Teoremi ve üçgenlerde benzerlik kullanılır. Burada aynı merdiven iki farklı konumda durmaktadır. Merdivenin boyu değişmez, ancak duvara olan yatay ve dikey uzaklıkları değişir. Şekil-1’deki eğimi 3/5; Şekil-2’deki eğimi 5/3 olarak verilmiştir. Ayrıca, Şekil-2 konumunda merdivenin tabanı ile duvar arasında 90 cm mesafe olduğu bilgisi vardır. Merdiven, bu konuma getirilirken tabanı h cm kaydırılmıştır. Aşağıdaki adımlar ve tablolar yardımıyla bu h değerini sistematik biçimde bulabiliriz.

1. Eğimi Anlama ve Değişkenleri Tanımlama

Bir üçgende “eğim” (özellikle merdivenin tabanı ile ulaştığı yükseklik arasında) genellikle şu şekilde yorumlanabilir:

  • Eğim = (Dikey Uzaklık) / (Yatay Uzaklık)

Bu problemde:

  • Şekil-1’de: eğim = 3/5

    • Eğer tabanın duvardan yatay uzaklığına x_1 dersek, dikey uzaklık y_1 olur ve
      $$\frac{y_1}{x_1} = \frac{3}{5} \implies y_1 = \frac{3}{5} , x_1.$$

  • Şekil-2’de: eğim = 5/3

    • Eğer tabanın duvardan yatay uzaklığına x_2 dersek, dikey uzaklık y_2 olur ve
      $$\frac{y_2}{x_2} = \frac{5}{3} \implies y_2 = \frac{5}{3} , x_2.$$

Ayrıca, merdivenin boyu (L) her iki durumda da aynıdır. Dolayısıyla, Şekil-1 ve Şekil-2’de Pisegör Teoremi (dik üçgen) açısından:

  1. Şekil-1 için:
    L^2 = x_1^2 + y_1^2.
  2. Şekil-2 için:
    L^2 = x_2^2 + y_2^2.

2. Şekil-1 İçin Pisegör Denklemi

Şekil-1’de:

  • y_1 = \tfrac{3}{5} x_1 olarak tanımladık.

Dolayısıyla,

L^2 = x_1^2 + y_1^2 = x_1^2 + \left(\frac{3}{5} x_1\right)^2 = x_1^2 + \frac{9}{25} \, x_1^2 = x_1^2 \left(1 + \frac{9}{25}\right) = x_1^2 \left(\frac{25}{25} + \frac{9}{25}\right) = x_1^2 \left(\frac{34}{25}\right) = \frac{34}{25}\, x_1^2.

Dolayısıyla,

L = \sqrt{\frac{34}{25}} \, x_1 = \frac{\sqrt{34}}{5} \, x_1.

3. Şekil-2 İçin Pisegör Denklemi

Şekil-2’de:

  • y_2 = \tfrac{5}{3} x_2 olarak tanımladık.

Dolayısıyla,

L^2 = x_2^2 + y_2^2 = x_2^2 + \left(\frac{5}{3} x_2\right)^2 = x_2^2 + \frac{25}{9}\, x_2^2 = x_2^2 \left(1 + \frac{25}{9}\right) = x_2^2 \left(\frac{9}{9} + \frac{25}{9}\right) = x_2^2 \left(\frac{34}{9}\right) = \frac{34}{9}\, x_2^2.

Dolayısıyla,

L = \sqrt{\frac{34}{9}}\, x_2 = \frac{\sqrt{34}}{3}\, x_2.

4. Aynı Merdivenin Boyunu Kullanarak x_1 ve x_2 Arasındaki İlişkiyi Bulma

Merdivenin boyu, her iki durumda da aynı olduğu için, L^2 değerleri birbirine eşittir:

\frac{34}{25}\, x_1^2 = \frac{34}{9}\, x_2^2.

Her iki tarafta 34 ortak çarpan olarak bulunduğundan, \frac{34}{25} x_1^2 = \frac{34}{9} x_2^2 \implies sadeleştirme yaptıktan sonra:

\frac{1}{25} x_1^2 = \frac{1}{9} x_2^2 \quad\Longrightarrow\quad 9\, x_1^2 = 25\, x_2^2 \quad\Longrightarrow\quad x_2^2 = \frac{9}{25} \, x_1^2 \quad\Longrightarrow\quad x_2 = \frac{3}{5} \, x_1.

Böylece, Şekil-2’deki yatay uzaklık, Şekil-1’deki yatay uzaklığın \tfrac{3}{5} katı olmalıdır.

5. Verilen 90 cm Bilgisini Yorumlama

Soruda, Şekil-2 konumunda merdiven ile duvar arasında 90 cm mesafe olduğu söyleniyor (Şekil’de 90 cm ibaresi yatayda gösterilmiştir). Bu durum, merdivenin tabanının duvardan uzaklığının 90 cm olduğunu belirtir. Yani:

x_2 = 90\ \text{cm}.

Önceki denklemimize göre x_2 = \tfrac{3}{5} x_1, o hâlde:

90 = \frac{3}{5} \, x_1 \quad\Longrightarrow\quad x_1 = \frac{90 \times 5}{3} = 150\ \text{cm}.

Demek ki ilk konumda taban, duvardan 150 cm uzaktaymış.

6. Tabanın Ne Kadar Kaydırıldığı (h) Hesaplaması

Mehmet Usta, merdiveni Şekil-1 konumundan Şekil-2 konumuna getirirken tabanı h cm yer değiştirmiştir. İlk konumda yatay uzaklık x_1 = 150 cm iken, ikinci konumda yatay uzaklık x_2 = 90 cm olmuştur.

Soruya göre h, bu iki konum arasındaki farktır. Ancak dikkat etmek gerekir: Sorudaki ifade “h cm kadar yer değiştirilmiştir” derken, taban 150 cm uzaklıktan 90 cm uzaklığa geçiyorsa, tabanın duvara doğru yaklaştığını görürüz. Dolayısıyla yer değiştirme miktarı:

h = x_1 - x_2 = 150 - 90 = 60 \ \text{cm}.

Seçeneklerdeki değerlerle karşılaştırdığımızda, 60 cm’nin A seçeneğine karşılık geldiğini fark ederiz.

7. Adım Adım Özet Tablolar

Aşağıdaki tablolar, hem Şekil-1 hem Şekil-2 için tanımları ve yapılan hesaplamaları özetlemektedir:

7.1 Şekil-1 (Eğim 3/5)

Adım Açıklama Denklem/Değer
1. Yatay Uzaklık x_1 Bilinmiyor
2. Dikey Uzaklık y_1 = \frac{3}{5}x_1 Eğimden (3/5)
3. Merdiven Boyu (Pisegör) L^2 = x_1^2 + y_1^2 L^2 = x_1^2 + \left(\frac{3}{5} x_1\right)^2
4. L^2 Açılımıyla Basitleştirme L^2 = x_1^2 + \frac{9}{25}x_1^2 = \frac{34}{25} x_1^2

7.2 Şekil-2 (Eğim 5/3)

Adım Açıklama Denklem/Değer
1. Yatay Uzaklık x_2 Bilinmiyor
2. Dikey Uzaklık y_2 = \frac{5}{3}x_2 Eğimden (5/3)
3. Merdiven Boyu (Pisegör) L^2 = x_2^2 + y_2^2 L^2 = x_2^2 + \left(\frac{5}{3} x_2\right)^2
4. L^2 Açılımıyla Basitleştirme L^2 = x_2^2 + \frac{25}{9} x_2^2 = \frac{34}{9} x_2^2
5. Verilen Bilgi (90 cm) x_2 = 90 cm Problemde şekilden alınan değer

7.3 İki Konum Arasındaki İlişki

Eşitlik Açıklama
\frac{34}{25} x_1^2 = \frac{34}{9} x_2^2 Aynı merdivenin boyu (L) her iki konumda eşit
Sadeleştirme sonucu x_2 = \frac{3}{5} x_1
Verilen x_2=90 cm Bu denklem kullanılarak x_1=150 cm bulunur
Yer değiştirme h = x_1 - x_2 = 150 - 90 = 60 cm

8. Sonuç

Yukarıdaki tüm adımlar birleştirildiğinde, Mehmet Usta’nın merdivenin tabanını h = 60 cm kaydırdığı sonucuna ulaşılır. Sorudaki şıklara bakıldığında bu değer, A) 60 seçeneğinin karşılığıdır.

Doğru cevap: 60 cm (A Şıkkı).

9. Kısa Özet

  1. Şekil-1’de eğim 3/5 olduğundan y_1 = \tfrac{3}{5}x_1 ve merdiven boyu L^2 = x_1^2 + \left(\tfrac{3}{5}x_1\right)^2 = \tfrac{34}{25}x_1^2 şeklinde bulunur.
  2. Şekil-2’de eğim 5/3 olduğundan y_2 = \tfrac{5}{3}x_2 ve merdiven boyu L^2 = x_2^2 + \left(\tfrac{5}{3}x_2\right)^2 = \tfrac{34}{9}x_2^2 şeklinde bulunur.
  3. Aynı merdiven kullanıldığı için \tfrac{34}{25}x_1^2 = \tfrac{34}{9}x_2^2 \implies x_2 = \tfrac{3}{5}x_1.
  4. Verilen bilgiye göre yeni konumda x_2 = 90 cm, buradan x_1 = 150 cm olur.
  5. Taban h cm yer değiştirdiğinden h = 150 - 90 = 60 cm.

Dolayısıyla aranan h = 60 cm’dir.

@zerrin_tuncel