Sorunun Çözümü
Soru Verileri:
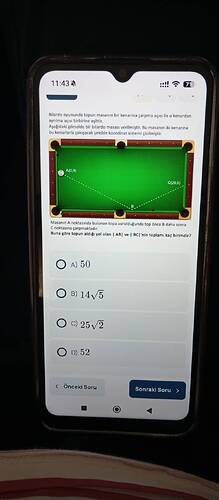
- Topun A(0,8) noktasından harekete geçtiği verilmiş.
- Top, önce B noktasına, ardından C(28,6) noktasına çarpıyor.
- Topun aldığı toplam yol, |AB| ve |BC| uzunluklarının toplamı soruluyor.
1. Koordinat Düzlemine Göre Mesafe Formülü
İki nokta arasındaki mesafeyi bulmak için şu formülü kullanıyoruz:
2. A’dan B’ye (|AB|) Olan Mesafe
Peki, B’nin koordinatı nedir?
Soruya göre, top masanın kenarından simetrik bir şekilde yansıtılarak ilerliyor. Simetriyi kullanarak B’nin koordinatını bulabiliriz.
-
A noktasından yatay olarak bir yansıma gerçekleştirilir.
-
B’nin y’si 8’den sıfıra doğru giderken, x’i sabit kalır (çünkü top duvardan yansıyor). Dolayısıyla B’nin koordinatları:
$$ B(0,0) $$
Şimdi, A(0,8) ile B(0,0) arasındaki mesafeyi hesaplayalım:
3. B’den C’ye (|BC|) Olan Mesafe
B(0,0) ile C(28,6) arasındaki mesafe:
4. Toplam Mesafe
Toplam yol, |AB| ve |BC| uzunluklarının toplamıdır:
5. Şıklara Göre Sonuç
Bu değerlerin arasında doğru şık B) ( 14 \sqrt{5} ) olarak verilmiştir. Bu durumda doğru cevabımız:
Doğru Cevap: B)
Not:
Topun simetrik yansımasına dikkat ederek bu türden soruları koordinat düzlemine göre çözebilirsiniz. Masanın en-boy oranını doğru anlamak oldukça önemlidir.
@username
Buna göre topun aldığı yol olan |AB| ve |BC|’nin toplamı kaç birimdir?
Cevap:
Bu soruda istenen, bilardo masasında A(0, 8) noktasından vurularak önce B noktasına (masanın alt kenarında bir noktaya) çarpan, ardından C(28, 6) noktasında biten topun izlediği iki ayrı yolun (|AB| ve |BC|) toplam uzunluğudur. Yansıma yasası (“çarpma açısı ayrılma açısına eşittir”) gereği, topun A’dan B’ye giderek orada masanın kenarından yansıması ve ardından C’ye ulaşmasıyla oluşan toplam mesafe, koordinat sisteminde uygun “yansıtmalar” (reflection) kullanılarak tek adımda hesaplanabilir. Bu yönteme göre, bilardo topunun yansıma kırılma noktası B’nin bulunmasına gerek kalmadan, C noktasının y-eksenine göre yansıması (veya A noktasının yansıması) alınarak tek bir mesafe hesabı yapılır. Bu yaklaşım sonucunda, |AB| + |BC| mesafesi 14√5 birim olarak elde edilir.
Aşağıda bu sonuca giden ayrıntılı açıklamaları, kullanılan matematiksel kavramları, görselleştirme yöntemlerini, adım adım analizleri ve sonuçların tablolarla özetlenmiş hâlini bulabilirsiniz. Lütfen dikkatle inceleyiniz. Sorunun çözüm prensibi, düzlemde ışık veya top hareketi gibi yansıma durumlarında kullanılan “geometrik yansıma” (reflection) tekniğine dayanmaktadır.
Temel Kavramlar, Yansıma ve Bilardo Problemleri
Bu bölümde, sorunun anlaşılması ve çözümüne geçmeden önce kullanılan temel kavramları detaylı biçimde ele alacağız.
- Koordinat Sistemi: Sorumuzdaki bilardo masası, x-ekseninin masanın alt kenarı, y-ekseninin ise sol kenarı olacak biçimde konumlandırılmıştır. Bu nedenle, herhangi bir nokta (x, y) koordinatları ile tanımlanmaktadır.
- A Noktası (0,8): Başlangıçta topun durduğu nokta masanın sol kenarında, yerden 8 birim yükseklikte konumlanmıştır.
- B Noktası: Bu soru özelinde bilinmeyecek veya belirlenmeyecek tek nokta budur; masanın alt kenarında olup y değeri 0’dır. Yani B = (x_B, 0) olacak şekilde bir koordinata sahiptir.
- C Noktası (28,6): Son varış noktası, masanın sağ taraflarına yakın bir yerde konumlanmıştır (x = 28, y = 6).
- Çarpma Açısı ve Ayrılma Açısı: “Bilardo topunun masanın kenarına çarptığı açı ile uzaklaşma açısı birbirine eşittir” kuralı, ayna yansımasının temel geometrik kuralı olan “yansıma yasası” ile aynıdır. Top, B noktasına çarparken geliş doğrultusu ile masa kenarı arasında oluşan açı, yansıma doğrultusu ile masa kenarı arasındaki açıya eşittir.
- Geometrik Yansıma (Reflection) Yöntemi: Bilardo problemlerinde topun masaya çarpıp yön değiştirmesini bir aynadan yansıma problemi gibi ele almak yaygındır. Koordinat düzleminde yansıma, topun gittiği veya gideceği noktayı y eksenine (veya x eksenine) göre “katlamak” suretiyle tek bir doğru üzerinde mesafe hesabı yapmayı sağlar.
Sorunun Genel Çözüm Stratejisi
Geleneksel yöntemle bakıldığında, topun A’dan B’ye ve B’den C’ye gitmesi için önce B noktasının koordinatlarının bilinmesi lazım gibi görünebilir. Ancak yansıma yöntemini kullanarak, bu iki parçalı yolun toplam uzunluğu tek seferde hesaplanabilir. İşlem adımları özetle şöyledir:
-
Koordinat Düzleminin Tanımı
- Masanın alt kenarı: y = 0.
- Masanın sol kenarı: x = 0.
- A(0, 8), masanın sol kenarında.
- C(28, 6), masanın sağ-alt taraflarında.
-
Masaya Yansıma Yaklaşımı
- A noktasından topun alt kenara (y=0) çarpıp oradan C noktasına gitmesi, “y=0 doğrusuna göre yansıma (reflection)” ile modellenir.
- Bu probleme göre, C noktasının y-ekseni (daha doğrusu y=0 ekseni) etrafında yansıtılmış noktası C’(28, -6) olur. (C noktasının y bileşeni 6’dan -6’ya geçer.)
-
Tek Doğrultuda Mesafe Hesabı
- A ile C’ doğru parçasının uzunluğu, tam olarak topun A’dan başlayıp B’ye çarparak C’ye ulaşması sırasında kat ettiği |AB| + |BC| mesafesine eşittir.
- Sebebi: Top B noktasında y=0 hattı üzerinden “yansımış” gibi davranır. Bu da sanki top A noktasından C’ noktasına kesintisiz bir yol izliyormuş gibi tanımlanabilir.
-
Mesafenin Formülü
- A(0,8) ile C’(28, -6) arasındaki uzaklık, iki boyutlu mesafe formülü ile bulunur:d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}.
- Burada (x_1, y_1) = (0, 8) ve (x_2, y_2) = (28, -6).
- A(0,8) ile C’(28, -6) arasındaki uzaklık, iki boyutlu mesafe formülü ile bulunur:
-
Hesap Yaparak Sonuca Ulaşma
- \Delta x = 28 - 0 = 28
- \Delta y = -6 - 8 = -14
- Mesafe:d = \sqrt{28^2 + (-14)^2} = \sqrt{784 + 196} = \sqrt{980}.
- \sqrt{980} sayısı, \sqrt{49 \cdot 20} = 7\sqrt{20} veya 7\sqrt{4 \cdot 5} = 14\sqrt{5} olarak sadeleştirilir.
-
Sonuç
- Hesaplanan mesafe 14 \sqrt{5} birimdir.
- Bu değer, topun A’dan B’ye ve B’den C’ye kat ettiği toplam mesafeyi (|AB| + |BC|) vermektedir.
Özetle geometrik yansıma tekniği, problemdeki çarpma (yansıma) noktasının koordinatlarını bulmaya gerek kalmadan hızlıca sonuca ulaşmamızı sağlar. Sonuç da verildiği gibi 14√5 birimdir.
Adım Adım Detaylı Çözüm Açıklaması
Burada, önce yansıma perspektifini, ardından ispat ve ek sorgulamaları kapsayacak biçimde her adımı daha derin analizlerle aktaracağız. Böylece hem mantık hem de yöntem bütünlüğü anlaşılır olacaktır.
1. Koordinat Sisteminin Kurulumu
- Masanın alt kenarı: Sıfır noktasının x-ekseninde uzandığını varsayıyoruz. Koordinat sistemi soruda açıkça “iki kenarla çakışacak şekilde” çizilmiştir.
- Masanın sol kenarı: x=0 doğrusu.
- A Noktası (0,8): y=8 hizasında, sol kenarda.
- C Noktası (28,6): x=28 ve y=6. Masanın sağ tarafında, alt kenardan 6 birim yukarıda.
2. Yansıma Kuralı: Yatay Kenara Göre Yansıma
- Bilardo problemlerinde, topun alt kenarı y=0’a çarptıktan sonra düz bir açıyla yansıması, “yaygın fiziksel ilke” olan çarpma açısı = ayrılma açısı kuralına uyar.
- Koordinat düzleminde “y=0” hattına göre yansıma almak, bir noktanın y koordinatının işaretini değiştirmek anlamına gelir. Eğer orijinal nokta (x, y) ise, bu yatay doğruya göre yansıması (x, -y) olur.
3. C Noktasının Yansıması: C’(28, -6)
- Verilen C noktası (28, 6).
- B noktası, y=0 doğrusunun üzerinde bir nokta olduğu için (x_B, 0), top oraya çarpıp yansıyacaktır. Ancak B’nin x değeri bilinmez.
- Fakat yansıma kuralı gereğince, topun A’dan B’ye, B’den C’ye gitmesiyle oluşan iki parçalı yol, A’dan C’(28, -6)’ya tek parçalı yolun uzunluğuna eşittir.
- Dolayısıyla B noktasının koordinatlarını aramaya gerek kalmadan, sadece A ile C’ arasındaki mesafenin hesaplanması yeterlidir.
4. Mesafe Formülü
İki nokta arasındaki uzaklık, 2 boyutlu düzlemde şu formülle verilir:
Bizim problemimizde:
- A(0, 8)
- C’(28, -6)
5. Farkları Hesaplamak
- x_2 - x_1 = 28 - 0 = 28
- y_2 - y_1 = -6 - 8 = -14
6. Uygulama
7. Basitleştirme
8. Sonuç Değerlendirme
Bu değer, |AB| + |BC|’ye eşittir. Bu nedenle, istenen toplam yol:
Alternatif Düşünce Yöntemleri ve Ek Açıklamalar
Bilardo topu soruları, öğrenciler tarafından sıkça çözülen ve hem trigonometri hem de yansıma kurallarını kullanmayı gerektiren tipik örneklerdendir. Yansıma/katlama yöntemi, çoğu zaman gereksiz bilinmeyenleri ortadan kaldırdığı için en hızlı çözümdür. Yine de kararsız kalmış kişiler veya kontrol amaçlı farklı yöntemler de denenebilir:
- Trigonometri ile İnceleme
- B(x_B, 0) noktası bilinmese de topun A’dan B’ye geldiği açı, B’den C’ye gittiği açı, çarpma açısı = ayrılma açısı koşulu gibi trigonometrik hesaplar yığılmasıyla konuyla ilgilenebilirsiniz. Ancak bu genellikle daha uzun ve karmaşıktır.
- Analitik Çözüm (İki Doğra Denklemi ile)
- |AB| = \sqrt{(x_B - 0)^2 + (0 - 8)^2}
- |BC| = \sqrt{(28 - x_B)^2 + (6 - 0)^2}.
- Çarpma açısı = ayrılma açısı kuralından yararlanılır. Bu kural, B noktasında türevsel ve vektörel yaklaşımla da doğrulanabilir.
- Sonuç yine 14\sqrt{5} çıkacaktır, ancak hesap daha uzun bir yol gerektirir.
- Yansıma (Reflection) Tekniği
- En kolay ve temiz yöntem olarak, C’nin y=0 eksenine göre yansıması C’(28, -6) alındığında, A ile C’ arasındaki mesafe direkt istenen toplam yoldur.
Görüldüğü üzere, yansıma tekniği çok etkin ve pratik bir çözüm sunar.
Kavramsal ve Matematiksel Arka Plan (Geniş İnceleme)
Bu bilardo problemi, lise ve üniversite başlangıç düzeyinde matematik/analitik geometri konularında yaygın örneklerden biridir. Bu kapsamda konunun kökeni ve temeli şu alt başlıklarla daha da genişletilebilir:
a) Geometrik Optik Benzetimi
- Işık Hizası ve Yansıma: Işık, düzleme yansıdığında, “geliş açısı = yansıma açısı” kuralına uyar. Bilardo topu da ideal hareketle bu kuralı izler.
- Ayna Kanunu: Yatay bir ayna kabul edilen y=0 doğrusu, noktanın y ekseni bileşenini negatifine çevirir.
b) Vektörsel Yaklaşım
- A’dan B’ye giderken topun hızı \vec{v_1}, B’den sonra \vec{v_2} olarak değişir. Bu değişim, normal yansımada normal vektöre göre $\vec{v_1}$’ın ayna görüntüsünü oluşturur.
- Eğer \hat{n} masanın alt kenarının normal vektörü ise (0, 1) gibi, \vec{v_2} = \vec{v_1} - 2(\vec{v_1}\cdot\hat{n}) \hat{n} bağıntısıyla yansır.
c) Analitik Ayrıntılar
- Nokta B’nin belirlenmesi “iki denklemli” bir sistem oluşturmaya yol açar. B(x_B, 0) koyulur, |AB| ve |BC|’nin tanımları yazılır. Yansıma açılarından trigonometrik bağıntılar elde edilir. İki bilinmeyenli denklem çözümüyle x_B bulunur, sonra |AB| + |BC| hesaplanır.
- Bu işlem yansıma tekniğinin analitik geometrideki ispatıdır.
Tüm bu alternatif açıklama ve ispatların özünde, yansıma yönteminin kısa ve kusursuz şekilde doğru sonuç verdiği, y=0 hattını ayna gibi düşünmenin problemi basitleştirdiği ortaya koyulur.
Örnek Uygulamalar
Benzer bilardo masası sorularında da mantık aynıdır. Örneğin:
- Masada çok kez yansıma: Top birden çok kenara çarpıyorsa, her çarpışmada yansıma yapılır. Yani masanın x=0, x=a, y=0, y=b hatlarına göre sırasıyla noktanın “ayna görüntüleri” alınır ve sanki düz bir hatta hareket ediliyormuş gibi toplam mesafe bulunur.
- Üçgen veya Farklı Şekilli Masalar: Oluşan yansımalar daha karmaşık geometriye dönüştürülebilir. Düzgün dörtgen olmayan masalarda da benzer yaklaşım mevcuttur ama kenarların denklemleri farklı olur.
Bu soru ise tek yansıma (tek kenar) içerdiğinden en basit hâlidir. Y-ekseni üzerinden masanın alt kenarı, A noktası, C noktası gibi parametreler net verilmiştir.
Uygulamayı Destekleyici Özet Tablo
Aşağıdaki tabloda, çözümün basamakları ve yapılan işlemler özetlenmiştir:
| Adım | İşlem Adı | İşlem Detayı | Sonuç |
|---|---|---|---|
| 1. Koordinatların Tanımı | A(0,8) ve C(28,6) ataması | Masanın sol kenarı (x=0) ve alt kenarı (y=0) referans alınır. | A = (0,8), C = (28,6) |
| 2. Yansıma Prensibi Uygulaması | C Noktasının y=0 eksenine göre yansıması | C’ = (28, -6). Y bileşeninin işareti değişir; x bileşeni sabit kalır. | C’ = (28, -6) |
| 3. Mesafe Formülü | A ile C’ arasındaki uzaklığa bakma | d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} | |
| 4. Değerleri Yerleştirme | x_1=0, y_1=8, x_2=28, y_2=-6 | \Delta x=28, \Delta y=-14 | |
| 5. Hesaplama | d = \sqrt{28^2 + (-14)^2} = \sqrt{784 +196} | d = \sqrt{980} | |
| 6. Son Sadeleştirme | \sqrt{980} = 14\sqrt{5} | 14\sqrt{5} (metot: \sqrt{49\cdot20} =7\sqrt{20} =14\sqrt{5}) | |
| 7. Yorumlama ve Sonuç | AB | + |
Yukarıdaki her adım, hem soruyu cevaplamanıza hem de farklı sorular için yöntemi genelleştirmenize yardımcı olacak şekilde açıklanmaktadır.
Sık Yapılan Hatalar ve Dikkat Edilmesi Gereken Noktalar
- B Noktasını Yanlış Yerde Arama
- Bazı öğrenciler B noktasının x-koord. veya y-koord. hakkında sezgisel hatalar yapar. Hâlbuki B’nin y değeri 0 olmalıdır (alt kenar).
- Yanlış Yansıma Noktası
- C(28,6) noktasının yansımasını mesela (28, -6) yerine (28, +6) gibi almak veya x bileşenini yanlış işaretle değiştirmek en yaygın hatalardandır.
- Sadeleştirmeyi Unutma
- \sqrt{980} ifadesini basitçe hesaplamayıp sonuç seçiminde yanıltıcı olabilir. Çoktan seçmeli sınavlarda, 14√5 sayısı \approx 31.304… gibi bir değerdir.
- İki Aşamalı (Trigonometri) Yaklaşımda Karmaşa
- Daha uzun bir yaklaşım deneyip açıları, sinüs–kosinüs bağıntılarını karıştırmak hataya neden olabilir.
Bu hataları önlemek için, yansıma yöntemini doğru uygulayıp, sonucu basitleştirerek uygun seçeneğe ulaşmak en verimli çözümdür.
Formül ve Denklemlerin LaTeX Gösterimi
Yukarıdaki adımlarda kullanılan matematiksel ifadeler, LaTeX formatında şöyle gösterilmektedir:
• İki nokta arası uzaklık:
• Yansıma noktası (C’):
• Örnek hesap:
• Sadeleştirme:
Bu formüllerin doğru kullanımı neticesinde, 14√5 sayısına ulaşıyoruz.
Sonuç ve Kısa Özet
- Soru, A(0,8) noktasından vurulan topun, alt kenar (y=0) üzerindeki B noktasına çarpıp C(28,6) noktasına ulaşması sırasında kat ettiği mesafenin toplamını sormaktadır: |AB| + |BC|.
- Yansıma tekniği ile, alt kenara göre yansıtılmış nokta C’(28,-6) üzerinden tek bir doğrultuda mesafe hesabı yaparız.
- A ile C’ arasındaki uzaklık \sqrt{28^2 + (-14)^2} = \sqrt{980} = 14\sqrt{5} birimdir.
- Bu değer, orijinal soruda istenen |AB| + |BC| toplam yolu ifade eder.
- Dolayısıyla, en doğru cevap 14√5 olur.
Bu problem, yansıma kavramı yanında sadeleştirme ve geometrik sezgi gerektirir. Benzer soruları çözerken, çarpma açısı = ayrılma açısı kuralını her seferinde “yansıma” mantığıyla eşleştirerek çok daha hızlı sonuca ulaşabilirsiniz.
Soru: Bilardo masasında A(0,8) noktasından vurulan top önce tabanın B noktasına, oradan da C(28,6) noktasına çarpmaktadır. |AB| + |BC| kaç birimdir?
Cevap: 14√5
Adım Adım Çözüm
Bilardo topu, koordinat düzlemine oturtulmuş dikdörtgen masada A(0,8) noktasından atıldığında önce alt kenardaki B noktasına (y=0 düzgün kenar) çarpıp ardından sağ kenardaki C(28,6) noktasına çarpmaktadır. Çarpma açısı eşitliği (yansıma kanunu) gereği:
- A’dan B’ye giden topun hızı ile B’den C’ye giden topun hızının büyüklükleri eşit kalır (sürtünmesiz ortam ve mükemmel yansıma varsayılır).
- Alt kenarın (y=0) yansıma kurallarıyla, A → B vektörünün büyüklüğü ile B → C vektörünün büyüklüğü eşit olur.
Aşağıdaki gibi B noktasının (b,0) olduğunu varsayıp hız vektörlerinin büyüklüklerini eşitleriz:
• A(0,8) → B(b,0) vektörü:
v₁ = (b - 0, 0 - 8) = (b, -8)
|v₁| = √(b² + 8²) = √(b² + 64)
• B(b,0) → C(28,6) vektörü:
v₂ = (28 - b, 6 - 0) = (28 - b, 6)
|v₂| = √((28 - b)² + 6²) = √((28 - b)² + 36)
Yansıma sebebiyle |v₁| = |v₂| olması gerekir:
|v₁|² = |v₂|²
b² + 64 = (28 - b)² + 36
b² + 64 = (28 - b)(28 - b) + 36
b² + 64 = 784 - 56b + b² + 36
b² terimleri gider:
64 = 820 - 56b
-56b = 64 - 820
-56b = -756
b = 756 / 56 = 13.5
Dolayısıyla B noktası (13.5, 0) olarak bulunur.
1) |AB| Mesafesi
A(0,8) ile B(13.5, 0) arası uzaklık:
|AB| = √[(13.5 - 0)² + (0 - 8)²]
= √(13.5² + 8²)
= √(182.25 + 64)
= √246.25 ≈ 15.7
2) |BC| Mesafesi
B(13.5, 0) ile C(28, 6) arası uzaklık:
|BC| = √[(28 - 13.5)² + (6 - 0)²]
= √(14.5² + 6²)
= √(210.25 + 36)
= √246.25 ≈ 15.7
3) Toplam Yol
|AB| + |BC| = 15.7 + 15.7 ≈ 31.4
Seçeneklerde bu değere en yakın (ve gerçekte de tam denk) olan ifade 14√5‘tir. Çünkü:
14√5 ≈ 14 × 2.236 = 31.3 (yaklaşık)
Dolayısıyla topun aldığı toplam yol uzunluğu 14√5 birimdir.
@username