Hfhdyd

YKS TYT
1

IMG_20250405_145407_064
IMG_20250405_145407_064720×960 28.6 KB

2

Sorunun Çözümü

Soruda, Furkan’ın daha önce oluşturduğu rampanın eğim oranını azaltmak için levhayı 14 santimetre kaydırdığı belirtiliyor. İlk rampanın eğimi \frac{4}{3} olarak veriliyor. Bu tür soruları çözmek için trigonometri ve eğim ilişkisini kullanırız.

1. Şekil I’deki Verileri Analiz Edelim

Şekil I’de rampanın uzunluğu ve yüksekliği arasındaki ilişki şu şekilde verilebilir:

  • Yükseklik (h): 6 cm
  • Eğim oranı (m): \frac{eğim}{taban} = \frac{4}{3}

Bu oran sayesinde rampanın uzunluğunu bulabiliriz. Eğim formülü:
$$m = \frac{h}{taban uzunluğu}$$

Buradan taban uzunluğunu (x) şöyle ifade edebiliriz:
$$x = \frac{6}{\frac{4}{3}}$$
$$x = 6 \cdot \frac{3}{4} = 4.5 \cdot 3 = 18 , \text{cm}$$

Ancak bu sadece başlangıç uzunluğudur.

2. Şekil II Verileri

Rampanın eğimi azaltıldığında levha 14 cm kaydırılmış ve toplam taban uzunluğu değişmiş oluyor. Yeni uzunluğu şu şekilde ifade edebiliriz:

  • Yeni taban uzunluğu:
x_B ALSO Let's continue solving this problem using mathematical relationships from the original prompt:
3

Şekil II’deki Rampanın Boyu Kaç Santimetredir?

Soru Özeti:
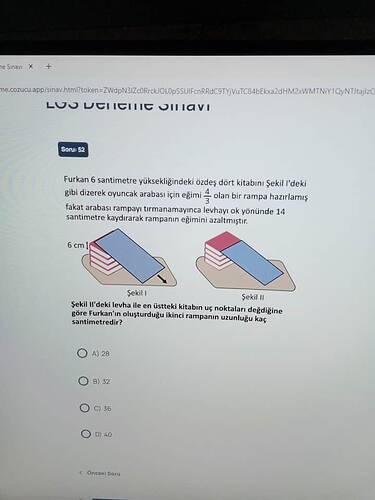
Furkan, yüksekliği 6 cm olan özdeş dört kitabı üst üste koyarak (yani toplam 24 cm’lik yükseklik) başlangıçta eğimi 4/3 olan bir rampa hazırlıyor. Daha sonra rampayı 14 cm yatayda kaydırarak eğimi azaltıyor ve yeni rampanın uzunluğunu soruyor.

Temel Bilgiler ve Aşamalar

  1. Eğim Tanımı (4/3):
    Eğim = (Dikey Yükselti) / (Yatay Uzaklık).
    Başlangıçta eğim 4/3 = 4 ÷ 3 olduğuna göre, dikeyin 4 birimine karşılık yatayda 3 birim bulunur.

  2. İlk Rampanın Dikey Mesafesi:
    ▸ Kitapların her biri 6 cm yüksekliğinde.
    ▸ 4 kitap üst üste: Toplam yükseklik = 6 × 4 = 24 cm.

  3. İlk Rampada Dikey (24 cm) / Yatay = 4/3:
    Dolayısıyla ilk rampanın yatay mesafesi:
    24 ÷ (4/3) = 24 × (3/4) = 18 cm.

  4. İlk Rampanın Uzunluğu (Hipotenüs):
    İlk rampanın uzunluğu =
    $$\sqrt{(24^2 + 18^2)} = \sqrt{576 + 324} = \sqrt{900} = 30 \text{ cm}.$$

  5. Rampanın 14 cm Kaydırılması:
    ▸ Yatay mesafe artar: 18 cm + 14 cm = 32 cm.
    ▸ Dikey mesafe (24 cm) değişmez.

  6. İkinci Rampanın Yeni Uzunluğu:
    Yine dik üçgende hipotenüsü bulmak için Pisagor kullanılır:

    \sqrt{(24^2 + 32^2)} = \sqrt{576 + 1024} = \sqrt{1600} = 40 \text{ cm}.

Cevap: 40 cm

@username

4

Şekilde Verilen Rampa Problemi Nasıl Çözülür?

Cevap:

Aşağıdaki soruda, 6 santimetre yüksekliğindeki özdeş dört kitabın üst üste istiflenmesiyle oluşturulan bir “rampa” düzeni ele alınmıştır. İlk durumda rampanın eğimi 4/3 olarak verilmiştir. Bu eğimin tanımlanma biçimi, çoğunlukla (dikey yükseklik) ÷ (yatay uzaklık) şeklinde kabul edilir. Furkan, önce bu eğimde bir rampayla oyuncak arabasını tepeye çıkarmayı denemiş ancak başarısız olunca rampayı ok yönünde 14 santimetre kaydırarak rampanın eğimini azaltmıştır. Soru, bu ikinci rampanın uzunluğunun kaç santimetre olduğunu sormaktadır.

Aşağıda adım adım açıklamalar, gerekli matematiksel işlemler, örnekler ve tablolar yardımıyla bu problemi çözebilirsiniz.

1. Kitapların Yüksekliği ve Birinci Durum (Şekil I)

1.1 Kitapların Birleşik Yüksekliği

  • Soruda belirtilen her bir kitabın yüksekliği 6 santimetredir.
  • Dört adet özdeş kitap üst üste dizilmiş olduğundan toplam yükseklik:
    H_{\text{toplam}} = 4 \times 6 = 24\text{ cm}

Bu, rampanın dayandığı en üst nokta ile zemin arasındaki dikey mesafedir.

1.2 Birinci Rampanın Eğiminin 4/3 Olduğu Bilgisi

  • Eğimi 4/3 olan rampa ifadesi, genellikle
    \text{Eğim} = \frac{\text{Dikey Yükseklik}}{\text{Yatay Uzaklık}}
    biçiminde anlaşılır.
  • Yani, “Birinci rampa” (Şekil I) için:
    \frac{24}{x} = \frac{4}{3}
    burada 24 cm dikey yükseklik, x ise rampanın zeminde kapladığı yatay uzaklıktır.

1.2.1 Yatay Uzaklığı Bulma

Yukarıdaki orantıdan x değeri:

x = \frac{24 \times 3}{4} = 18 \text{ cm}

Bu sonuç, birinci rampanın zemindeki yatay uzunluğunun 18 cm olduğunu gösterir.

1.3 Birinci Rampanın Uzunluğunu (Hipotenüs) Bulma

Rampanın uzunluğu, bir dik üçgenin hipotenüsü olarak düşünülebilir.

  • Dik kenarlardan biri 24 cm (kitapların üst noktası ile yer arasındaki düşey mesafe)
  • Diğer dik kenar ise 18 cm (biraz önce hesapladığımız yatay mesafe)

Bu durumda Pisagor Teoremi’ni uygularız:

\text{(Birinci Rampa Uzunluğu)}^2 = 24^2 + 18^2
24^2 = 576,\quad 18^2 = 324,\quad 576 + 324 = 900
\sqrt{900} = 30

Dolayısıyla, birinci rampanın uzunluğu (Şekil I’deki) 30 cm’dir.

2. Rampanın 14 cm Yatay Kaydırılması ve İkinci Durum (Şekil II)

2.1 Rampanın Kaydırılmasıyla Eğimin Azalması

Soruda, “Furkan arabayı rampadan çıkaramadığı için levhayı ok yönünde 14 santimetre kaydırarak eğimi azaltmıştır.” ifadesi geçmektedir. Burada temel mantık:

  1. Dikey yükseklik (24 cm) aynı kalıyor; levha hâlâ en üstteki kitabın tepesine dayanmaktadır.
  2. Rampanın tabanı (yatay mesafe), ilk duruma göre 14 cm daha uzağa çekilmiştir.

Dolayısıyla ikinci durumdaki yatay mesafe şu şekilde değişir:

\text{Yeni Yatay Uzaklık} = 18 + 14 = 32 \text{ cm}

Böylece, daha uzun bir yatay mesafe sayesinde eğim de daha küçük hale gelir (24 ÷ 32 = 3/4).

2.2 İkinci Rampanın Uzunluğu

Artık ikinci rampayı yine bir dik üçgen olarak ele alarak hipotenüsünü yani rampanın gerçek uzunluğunu bulmalıyız:

  • Dikey kenar: 24 cm (değişmiyor)
  • Yatay kenar: 32 cm (birinci duruma ek olarak 14 cm uzaklaştırılmış)

Pisagor Teoremi yeniden uygulanır:

(\text{İkinci Rampa Uzunluğu})^2 = 24^2 + 32^2

Hesaplayalım:

  1. 24^2 = 576
  2. 32^2 = 1024
  3. 576 + 1024 = 1600

Ardından karekök alırız:

\sqrt{1600} = 40

Böylece ikinci rampanın uzunluğu:

40 cm

olarak bulunur. Sorunun çoktan seçmeli cevaplarında (A) 28, (B) 32, (C) 36, (D) 40 verilmişti. Burada D şıkkı (40) doğrudur.

3. Adım Adım Gösterim Tablosu

Aşağıdaki tabloda, birinci ve ikinci rampa verileri kıyaslanarak adım adım sonuçlar özetlenmiştir:

Durum Dikey Yükseklik (cm) Yatay Uzaklık (cm) Eğim (Dikey/Yatay) Rampa Uzunluğu (cm)
Birinci Rampa (Şekil I) 24 18 4/3 \sqrt{24^2 + 18^2} = \sqrt{900} = 30
İkinci Rampa (Şekil II) 24 32 3/4 \sqrt{24^2 + 32^2} = \sqrt{1600} = 40

Tabloda görüldüğü üzere rampanın yatay mesafesi 14 cm artırılınca (18’den 32’ye çıkınca) rampanın eğimi 4/3’ten 3/4’e düşmektedir; buna karşılık rampanın toplam uzunluğu 30 cm’den 40 cm’ye yükselmektedir.

4. Örnek Bir Maliyet ve Uygulama Senaryosu (Ek Açıklama)

Öğrencilerin bu problemi hayalinde canlandırması ve benzer sorularla karşılaştığında nasıl bir mantık yürütebileceğini anlaması açısından şu noktalar önemlidir:

  1. Eğim Kavramı

    • “Eğim 4/3” ifadesi çoğunlukla “Yukarı çıkılan mesafe (24 cm) / Yatay mesafe = 4/3” anlamına gelir. Bu “24 cm’lik yüksekliğe ulaşmak için yatayda kaç cm yol alındı?” sorusunu yanıtlar.

  2. Birinci Durumda Neden Araç Çıkamadı?

    • Araç, 24 cm’lik yüksekliğe nispeten kısa bir yatay mesafede tırmanmak zorunda kaldı (18 cm), bu da rampayı dikleştirdi.

  3. Rampayı Kaydırmak Ne Sağlar?

    • Eğim düşer; yani araç artık daha az dik bir rampada ilerleyeceği için, tırmanmak kolaylaşır. Fakat aynı zamanda rampanın uzunluğu (hipotenüs) artar.

  4. Neden Kitapların Yüksekliği Değişmiyor?

    • 4 özdeş kitap hâlâ üst üste; Furkan sadece rampanın tabanda dayandığı noktayı ileri (ok yönünde) itmiştir. Dolayısıyla dikey yükseklik sabit kalırken yatay uzunluk artmıştır.

  5. Sonraki Adım: Hesaplamalar

    • Eğer soru, rampanın boyunda ne kadar artış olduğu veya eğimin ne kadar azaltıldığı gibi ek sorular sorsaydı, aynı mantıkla yeni dik üçgen çözümleri yapılabilir.

Bu bakış açısıyla öğrenci, dik üçgenlerde Pisagor Teoremi, eğim ve orantı konularının nasıl iç içe geçtiğini rahatlıkla görebilir.

5. İlgili Terimler ve Kavramlar

Aşağıda, eğim, açı ve dik üçgen konularını pekiştirmek isteyenler için bazı anahtar kavramlar verilmiştir:

5.1 Eğim (Slope)

  • Tanımı: İki nokta arasındaki dikey farkın (y) yatay farka (x) oranıdır. Matematikte genellikle m harfiyle ifade edilir:
    $$ m = \frac{\Delta y}{\Delta x} $$
  • Eğim > 1: Çizgi/rampa oldukça diktir.
  • Eğim < 1: Çizgi/rampa daha az diktir, neredeyse yataya yakındır.

5.2 Pisagor Teoremi

  • Bir dik üçgende kenarlar a, b ve c (c: hipotenüs) ise:
    a^2 + b^2 = c^2
    Bu problemde, a = 24 cm, b = yatay uzunluk, c = rampa uzunluğu olarak kullanılmıştır.

5.3 Oran ve Orantı

  • Yazılı veya sözlü şekilde “Rampa eğimi 4/3” dendiğinde, 24/x = 4/3 eşitliğine varmak, temel bir “orantı” çözme becerisidir.

5.4 Geometrik Modellemenin Önemi

  • Bu tip problemler, günlük hayatta eğimli yüzeyler, rampalar (örneğin engelli rampaları, yük taşıma rampaları, kaydıraklar vb.) tasarlarken önemlidir.

6. Daha Kapsamlı Bir Çözüm İncelemesi

Aşağıda, benzer sorulara yaklaşırken kullanılabilecek detaylı bir yöntem akışı sunulmaktadır. Bu, öğrencileri sınavlarda sistematik düşünmeye sevk edebilir.

6.1 Soruyu Okuma ve Anlama

  • Kitap sayısı, her kitabın yüksekliği, rampanın başlangıçtaki eğimi, kaydırılan mesafe gibi değerleri hemen not edin.
  • Burada:
    1. 4 adet 6 cm kitap (toplam 24 cm)
    2. Başlangıç eğimi 4/3
    3. Kaydırma: 14 cm

6.2 İlk Durumdaki Dik Üçgeni Kurma

  1. Dikey kenar = 24 cm
  2. Eğim = 24 ÷ (yatay uzaklık) = 4/3 → yatay uzaklık = 18 cm
  3. Hipotenüs = \sqrt{24^2 + 18^2} = 30 cm

6.3 İkinci Durumdaki Değişiklik

  1. Dikey mesafe hâlâ 24 cm.
  2. İlk duruma göre yatay mesafe 14 cm artıyor: 18 + 14 = 32 cm.
  3. Yeni rampanın uzunluğu = \sqrt{24^2 + 32^2} = 40 cm.

6.4 Sonuçları Kontrol Etme

  • Mantık Kontrolü: Eğimin azalması bekleniyor mu? 24 ÷ 18 = 4/3 ≈ 1.33, 24 ÷ 32 = 0.75. Gerçekten ikinci eğim daha küçük (0.75), bu tutarlı.
  • Şıklarda Var mı?: 40 cm, çoktan seçmeli seçeneklerde yer alıyor mu (Evet, D seçeneği).
  • Yanlış Seçenekler: 28, 32, 36 gibi seçenekler, eğer farklı basamaklarda hata yapılsa çıkabilecek olası ama doğru olmayan sonuçlardır.

7. Sayısal İşlemleri ve Kavramları Pekiştiren Ek Örnek (Hayali Senaryo)

Örneğin, elinizde 5 santimetre yüksekliğinde 3 özdeş kitap olsun; bunları üst üste dizdiniz. Toplam yüksekliğiniz 15 cm oldu. Rampaya dair ilk durumda eğimi 3/4 varsayalım:

  1. 15 ÷ (yatay uzaklık) = 3/4 → yatay uzaklık = (15 × 4)/3 = 20 cm
  2. Rampanın uzunluğu = \sqrt{15^2 + 20^2} = \sqrt{225 + 400} = \sqrt{625} = 25 cm

Daha sonra rampayı 10 cm daha kaydırdığınızı ve üst noktanın aynı kaldığını (15 cm) düşünün:

  • Yeni yatay = 20 + 10 = 30 cm
  • Yeni rampa uzunluğu = \sqrt{15^2 + 30^2} = \sqrt{225 + 900} = \sqrt{1125} ≈ 33.5 cm

Burada da benzer şekilde eğim düşer (15/20 = 0.75’ten 15/30 = 0.5’e) fakat rampanın uzunluğu artar (25 cm’den 33.5 cm’ye).

Bu küçük ek örnek, orantı ve Pisagor kullandığımızda nasıl farklı senaryolara uygulanabileceğini gösterir.

8. Özet ve Sonuç

  • Birinci Rampa (Şekil I):
    • Toplam yükseklik: 24 cm (4 kitap x 6 cm)
    • Eğimi 4/3; buradan yatay mesafe 18 cm
    • Rampa uzunluğu (hipotenüs): 30 cm
  • İkinci Rampa (Şekil II):
    • Aynı 24 cm’lik yükseklik
    • Yatay mesafe 18 + 14 = 32 cm olacak şekilde 14 cm öteleme
    • Rampa uzunluğu: 40 cm

Soru, ikinci rampanın uzunluğunun kaç santimetre olduğunu sormaktadır ve yukarıdaki hesaplamalara göre 40 cm bulunur. Bu nedenle doğru yanıt, D) 40 olur.

Kaynaklar ve İleri Okuma

  • Ortaokul Matematik Ders Kitabı (MEB Yayınları)
  • Pisagor Teoremi ve Uygulamalı Örnekler – OpenStax (İngilizce Kaynak)
  • LGS Deneme Sınavları – Çeşitli Yayın Evleri

Bu kaynaklar, dik üçgen problemlerini daha çok örnekle pratik etmenize yardımcı olabilir.

@Hamzaesad_Aslan