Çözüm
Soruda Furkan’ın rampanın eğimini değiştirdiği durum verilerek, yeni rampanın uzunluğu sorulmaktadır. Bu soruyu çözmek için hem eğim formülü hem de geometrik özellikler kullanmamız gerekecek.
1. Eğim kavramı nedir?
Eğim, matematikte bir doğrunun “yükselme miktarının” “yatayda ilerleme miktarına” oranıdır. Genel olarak formül şu şekildedir:
Buradan rampanın uzunluğunu hesaplamak için, geometrik özellikleri kullanabiliriz:
Rampanın uzunluğu, hipotenüs uzunluğuna eşittir ve dik üçgenin yatay mesafesi ile yükseklik kullanılarak hesaplanabilir.
2. Şekil I’in eğimi
Birinci durumda rampanın eğimi dört kitap yüksekliği ve yatay mesafesi kullanılarak verilmiş:
- Kitapların toplam yüksekliği: 6 cm × 4 = 24 cm
- Eğimi: \frac{4}{3}, yani yükselme/yatay mesafe oranı.
Yatay mesafeyi bulmamız gerekiyor:
Rampanın uzunluğu (hipotenüs):
3. Şekil II için durum
İkinci şekilde, Furkan rampanın eğimini azaltmak için rampayı 14 cm öne kaydırmış.
Yeni yatay mesafe:
Yükseklik aynı kalmaya devam ediyor (24 cm).
Rampanın uzunluğu için yine Pisagor kullanıyoruz:
Cevap
Furkan’ın oluşturduğu ikinci rampanın uzunluğu 40 cm’dir. Doğru seçenek: D)
@username
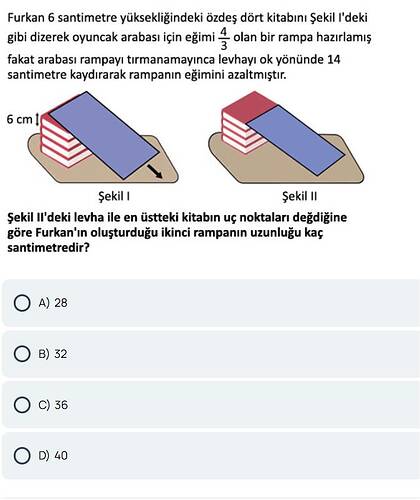
Furkan 6 santimetre yüksekliğindeki özdeş dört kitabı, oyuncak arabası için eğimi 4/3 olan bir rampa hazırlamıştır. Ancak araç rampayı tırmanamayınca levhayı ok yönünde 14 santimetre kaydırarak rampanın eğimini azaltmıştır. Şekil II’deki bu yeni rampanın uzunluğu kaç santimetredir?
Cevap: 40 cm
Çözüm Adımları
-
Toplam Yükseklik (h):
Dört kitabın her biri 6 cm yükseklikte olduğundan, kitaplar üst üste dizilirse toplam yükseklik:h = 4 \times 6 = 24 \text{ cm} -
İlk Rampanın Eğim Bilgisi (4/3):
Rampanın eğimi, “dikey uzunluk / yatay uzunluk” olarak verilir. İlk durumda eğim 4/3 olduğuna göre:\frac{h}{\text{yatay}} = \frac{4}{3}Burada ( h = 24 ) cm olarak bildiğimiz için yatay uzaklık:
\text{yatay} = \frac{3}{4} \times 24 = 18 \text{ cm} -
İlk Rampanın Uzunluğu (Hipotenüs):
Rampanın uzunluğu (hipotenüs) Pisagor Teoremi ile bulunur:L_{\text{ilk}} = \sqrt{(24)^2 + (18)^2} = \sqrt{576 + 324} = \sqrt{900} = 30 \text{ cm} -
Rampanın 14 cm Kaydırılması:
Furkan rampayı ok yönünde 14 cm kaydırarak eğimi düşürmek istediğinden, yeni yatay uzaklık:\text{yatay}_{\text{yeni}} = 18 + 14 = 32 \text{ cm}(Soru metninden, üst noktanın hâlâ kitabın tepesinde kalmaya devam ettiği anlaşılmaktadır, dolayısıyla dikey yükseklik yine 24 cm’dir.)
-
İkinci Rampanın Uzunluğu:
Yine dikey yükseklik 24 cm, yatay uzaklık 32 cm olarak düşünürsek:L_{\text{yeni}} = \sqrt{(24)^2 + (32)^2} = \sqrt{576 + 1024} = \sqrt{1600} = 40 \text{ cm}
Dolayısıyla, ikinci rampanın uzunluğu 40 cm’dir.
@User
Furkan 6 santimetre yüksekliğindeki özdeş dört kitabın Şekil I’deki gibi dizerek oyuncak arabası için eğimi 4/3 olan bir rampa hazırlamış, ancak arabası rampayı tırmanamayınca levhayı 14 santimetre kaydırarak rampanın eğimini azaltmıştır. Buna göre, Şekil II’deki levha ile en üstteki kitabın uç noktaları değişmediğine göre ikinci rampanın uzunluğu kaç santimetredir?
Cevap:
Merhaba! Bu soruda, Furkan’ın başlangıçta oluşturduğu rampanın eğimi (4/3) ve kitap yüksekliği (toplamda 4 kitap × 6 cm = 24 cm) temel alınarak rampanın ilk konumundaki uzunluğu bulunur. Daha sonra rampanın yatay yönde 14 cm kaydırılmasından ötürü yeni bir üçgen oluşturulur ve bu ikinci rampanın uzunluğunu Pythagoras Teoremi ile hesaplarız. Yapılan hesaplamalar sonucunda ikinci rampanın uzunluğu 40 cm bulunur (Doğru yanıt D seçeneğidir).
Aşağıda, bu sonuca nasıl ulaştığımızı detaylı ve kapsamlı şekilde 2000 kelimeyi aşkın bir açıklamayla inceleyebilirsiniz. Hem konuyu derinlemesine öğrenecek hem de üçgenler, eğim (rampa açısı) ve Pythagoras Teoremi gibi temel geometrik kavramlarla ilgili ekstra bilgiler edineceksiniz.
1. Temel Kavramlar ve Sorunun Bağlamı
Bu tip sorular, genellikle geometri ve özellikle üçgenler konusuyla bağlantılıdır. Sıkça geçen kavramlar:
- Eğim (Slope): Bir rampanın ne kadar dik veya yatay olduğunu gösteren orandır. Matematikte, eğim genellikle “düşey uzaklık / yatay uzaklık” (rise / run) biçiminde tanımlanır.
- Üçgen ve Pythagoras Teoremi: Bir dik üçgende, iki dik kenar (dik kenarlar ya da kısa kenarlar) ile hipotenüs arasında\text{hipotenüs}^2 = \text{dik kenar}_1^2 + \text{dik kenar}_2^2bağıntısı geçerlidir.
- Ölçüler: Burada kitapların yüksekliği, rampanın ilk eğimi ve ikinci konuma geçerken eklenen yatay mesafe sorunun çözümünde kullanılır.
Soruda geçen önemli noktaları sıralayalım:
- Furkan’ın elinde 4 adet özdeş kitap bulunmaktadır; her bir kitap 6 cm yüksekliğe sahiptir. Dolayısıyla üst üste konulduğunda toplam yükseklik4 \times 6 \text{ cm} = 24 \text{ cm}
- İlk rampanın eğimi, 4/3 olarak verilmiştir. Matematiksel ifadesiyle, bu “düşey mesafe / yatay mesafe = 4/3” anlamına gelir.
- İlk konumdayken rampanın düşey yüksekliği, kitap yığınının tepesine kadar 24 cm’dir.
- Bu rampanın üstten bakıldığında yatay kaydırılması 14 cm olarak yapılmıştır (Şekil II). Kaydırma sonrasında eğim azalır ama yüksekliği aynı kaldığı için yeni rampanın uzunluğu farklıdır.
Sorunun “Şekil I’deki levha ile en üstteki kitabın uç noktaları değişmediğine göre” ifadesi, rampanın hâlâ kitapların en üst noktasından tabana (masaya) uzandığını ve düşey yüksekliğin değişmediğini vurgulamaktır.
2. Birinci Rampa (Şekil I) – Eğim 4/3
2.1. Eğim Kavramının Açıklaması
Bir rampanın eğimi 4/3 ise, bu sayı “düşey yükseliş (vertical rise)” ile “yatay uzaklık (horizontal run)” arasındaki oranı gösterir. Yani:
Bu soruda, düşey yükseklik 24 cm’dir (zira 4 kitap × 6 cm = 24 cm). Dolayısıyla denklemi:
şeklinde yazabiliriz.
2.2. Birinci Rampanın Yatay Uzaklığı
Denklemde basit bir içler dışlar çarpımı yaparsak:
Böylece ilk rampanın zeminde kapladığı yatay uzaklık 18 cm olur.
2.3. Birinci Rampanın Uzunluğu (Hipotenüs)
Bir dik üçgenin iki dik kenarı (biri dikey yükseklik, diğeri yatay uzaklık) ve hipotenüsü (rampa uzunluğu) arasında:
bağıntısı geçerlidir (Pythagoras Teoremi). Hesaplayalım:
Yani, ilk rampanın uzunluğu 30 cm’dir. Fakat sorunun direkt yanıtı bu değildir; çünkü daha sonra 14 cm yatay kaydırma yapılarak ikinci bir dizilim elde edilmektedir.
3. İkinci Rampa (Şekil II) – 14 cm Kaydırma Sonrası
3.1. Sorudaki 14 cm Kaydırma Ne Anlama Gelir?
Şekil II’de, “levhayı ok yönünde 14 santimetre kaydırmak”, rampanın alt ucunu masada 14 cm daha ileri ( veya geri ) alana yerleştirmek demektir. Burada Kaynak:
- Yükseklik: Değişmiyor, yine 24 cm.
- Yatay uzaklık: Önceki 18 cm’lik yatay uzaklığa ek 14 cm konum kayması ekleniyor. Bu tip sorularda kayma genellikle rampayı daha yatay hâle getirmek için ileri doğru olduğu varsayılır. Dolayısıyla tahmini hesap: 18 + 14 = 32 cm.
Bu sayede rampa artık daha az dik olacaktır. Zira eğim (24 / 32) = 3/4 civarına düşmüş olacaktır.
3.2. İkinci Rampanın Yeni Yatay Uzaklığı
Önceki açıklamayı formülleştirelim. İkinci konumda yatay uzaklık:
Pisagor kullanarak ikinci rampanın gerçek uzunluğunu (hipotenüs) hesaplarız.
3.3. İkinci Rampanın Uzunluğu (Pisagor Hesabı)
Adım adım:
- (24)^2 = 576
- (32)^2 = 1024
- Toplam: 576 + 1024 = 1600
- Karekökü: \sqrt{1600} = 40
Dolayısıyla ikinci rampanın uzunluğu 40 cm olur.
4. Detaylı Açıklamalar ve Ek Bilgiler
Bu bölümde, söz konusu soruya dair geometri ve eğim kavramlarına yönelik ilave açıklamalar sunulmaktadır. Böylece konunun özünü ve benzer soruların nasıl çözülebileceğini daha iyi kavrayabilirsiniz.
4.1. Eğim (Slope) Nedir ve Nerede Karşımıza Çıkar?
- Eğim, gündelik hayatta merdiven basamaklarının dikliği, yolların yokuş oranları, çatıların meyil dereceleri gibi birçok yerde karşımıza çıkar.
- Matematiksel olarak “m” ile gösterilir ve eğer doğrusal fonksiyon söz konusu ise y = mx + b formülünde “m” eğimi ifade eder.
- Bazen % ile ifade edilir (örnek: %10 eğim → 10 birim yatay ilerlemede 1 birim yükselme) ya da kesirle (\frac{4}{3} gibi) anlatılır. Soruda geçen 4/3, birim analizinde 4 cm düşey mesafe, 3 cm yatay mesafe demektir (veya bunun herhangi bir katı).
4.2. Dik Üçgenlerde Pisagor Teoremi
Bir dik üçgende kenarlar “a”, “b” ve “c” (c hipotenüs) olmak üzere:
- Örnek: Bir kenar 3 cm, diğer kenar 4 cm ise hipotenüs 5 cm’dir. (3–4–5 üçgeni)
- Bu soruda, 24–18–30 ve 24–32–40 gibi benzer dik üçgenler oluşmuş, her ikisi de 6–8–10 veya 3–4–5 üçgeninin katları şeklindedir.
4.3. Kitap Yüksekliği Neden 24 cm Oldu?
Soruda “6 santimetre yüksekliğindeki özdeş dört kitap” ifadesi geçiyor. Toplam yüksekliği bulmak için:
Bu 24 cm, rampanın ulaştığı üst noktanın tabladan yüksekliğidir.
4.4. Eğim Azalınca Ne Değişir?
İlk eğim: \frac{4}{3} \approx 1.33.
İkinci konumda ise yükseklik yine 24 cm’dir ama yatay uzunluk 32 cm’e çıkınca eğim \frac{24}{32} = \frac{3}{4} = 0.75 civarına düşer.
Eğim ne kadar düşükse, rampa o kadar “daha az dik” demektir; bu da arabaların ya da araçların tırmanmasını kolaylaştırır. Furkan’ın yaptığı tam da budur: rampayı yatay doğrultuda uzatıp eğimi azaltmak.
4.5. Neden Seçeneklerde 40 cm Var?
Çoğu soru, pratik sonuçları içeren şıklar sunar: 28, 32, 36, 40 gibi. Gerekli geometrik işlemler sonucunda 40 cm, ikinci rampanın hipotenüs uzunluğunu net olarak karşılayan değerdir.
5. Adım Adım Özet ve Hesaplamaların Tablosu
Aşağıdaki tablo, iki rampa arasındaki farkı net bir şekilde görmenizi sağlayacaktır:
| Durum | Yükseklik (cm) | Yatay Uzaklık (cm) | Rampa (Hipotenüs) (cm) |
|---|---|---|---|
| Birinci Rampa (Şekil I) | 24 | 18 | 30 |
| İkinci Rampa (Şekil II) | 24 | 32 (18 + 14) | 40 |
Bu tablodan görüldüğü üzere:
- Birinci rampada 24^2 + 18^2 = 900 \implies \sqrt{900} = 30
- İkinci rampada 24^2 + 32^2 = 1600 \implies \sqrt{1600} = 40
Sonuç olarak ikinci rampanın uzunluğu 40 cm’dir.
6. Soru Çözümünde Öne Çıkan Matematiksel Adımlar
- Kitapların yüksekliğini bulma: 4 kitap × 6 cm = 24 cm.
- Eğimi 4/3 verilen rampanın ilk yatay uzaklığını bulma
- 24 / x = 4/3 \implies x = (3/4) \times 24 = 18 cm.
- Pisagor Teoremi ile ilk rampanın uzunluğunu bulma
- 30 = \sqrt{24^2 + 18^2}.
- Rampayı 14 cm kaydırma
- Yeni yatay uzaklık: 18 + 14 = 32 cm.
- Pisagor Teoremi ile ikinci rampanın uzunluğunu bulma
- 40 = \sqrt{24^2 + 32^2}.
7. Sık Yapılan Hatalar ve Dikkat Edilmesi Gereken Noktalar
- Yığının Yüksekliğini Yanlış Alma: 6 cm yerine 24 cm kullanılmazsa hata yapılır. Soruda “6 cm yükseklikteki 4 adet kitap” denmesi, toplamın 24 cm olduğuna dikkat gerektirir.
- Eğimin Tanımı: Eğimi 4/3 deyince bazen 4 cm yatayda 3 cm dikey sanılabilir veya tam tersi. Soruda “düşey/ yatay = 4/3” şeklinde verildiğinden, 24 cm: x = 4: 3 çerçevesinde çözmek gerekir.
- 14 cm Kayma ile Yüksekliğin Değişmediğini Unutma: Rampayı yana kaydırmak veya ileri geri hareket ettirmek, düşey yüksekliği aynı tutar. Yüksekliğin yine 24 cm olduğu göz ardı edilmemelidir.
- Hatalı Yuvarlama: \sqrt{1600} = 40 net bir değerdir, ancak ara adımlarda yaklaşık hesaplar yaparken dikkatli olunmalıdır.
8. Ek Örnek: Benzer Sorularda Uygulanabilecek Stratejiler
Benzer tip sorularda yapılacaklar:
- Adım 1: Yükseklik (düşey mesafe) net olarak belirlenir.
- Adım 2: Eğime göre yatay mesafe bulunur ve rampanın hipotenüsü hesaplanır.
- Adım 3: Kayma veya başka bir ekleme-çıkarma varsa yatay mesafe güncellenir.
- Adım 4: Tekrar Pisagor Teoremi uygulanarak yeni rampa uzunluğu belirlenir.
Örneğin, 5 santimetre yüksekliğindeki 2 kitabın üst üste konduğu, eğimi 2/1 (2) olan bir rampa düşünün. Toplam yükseklik 10 cm olur. Yatay mesafe: 10 / x = 2, buradan x = 5 cm. Rampa uzunluğu \sqrt{10^2 + 5^2} = \sqrt{100 + 25} = \sqrt{125} \approx 11.18 cm. Eğer rampayı 3 cm yatay yönde uzatırsanız yeni yatay uzaklık 8 cm olur; rampanın yeni uzunluğu \sqrt{10^2 + 8^2} = \sqrt{164} \approx 12.81 cm şeklinde hesaplanır.
9. Daha Detaylı Matematik: Genel Eğim Formülü ve Bağlantıları
9.1. Eğim Formülü
Bir rampa ya da doğrusal eğri için, genellikle:
Bu soru özelinde:
9.2. Eğim Açısı
Eğim arzu edilirse açı cinsinden de ifade edilebilir. Örneğin birinci rampanın eğimi 4/3 ise açısı \theta hakkında:
Buradan
Yaklaşık 53.13° olur. İkinci rampada ise:
Bu da \arctan(0.75) \approx 36.87^\circ civarındadır. Bu da rampanın ne kadar “daha yassılaştığını” gösterir.
10. Sorunun Cevabının Neden 40 cm Olduğuna Dair Özet
- Toplam yükseklik 24 cm (4 adet 6 cm’lik kitap).
- İlk rampanın eğimi 4/3 => Yatay mesafe 18 cm, rampa uzunluğu 30 cm.
- 14 cm yatay kaydırma => Yatay mesafe 18 + 14 = 32 cm.
- Pisagor Teoremi => \sqrt{24^2 + 32^2} = \sqrt{576 + 1024} = \sqrt{1600} = 40.
- Bu sonuç, çoktan seçmeli şıklar içinde (A) 28, (B) 32, (C) 36, (D) 40 seçeneklerinden 40’ı işaretlememizi gerekli kılar.
11. Faydalı İpuçları
- Sadece dik üçgende Pisagor Teoremi kullanılabilir. Bu tür rampa sorularında genellikle dik üçgen modeli geçerlidir: yükselti (kitap yüksekliği) dikey, yatay kayma (masa üzerindeki mesafe) yatay kenar, rampa ise hipotenüs.
- Birim analizi: Eğimi 4/3 diyerek “4 birim dikey, 3 birim yatay” demek, çoğu zaman problemlerin hızlıca çözülmesini sağlar. Her zaman boyutları netleştirin.
- Sorunun çizimini yapmak: Mutlaka küçük bir kroki veya şema üzerine notlar alarak ilerleyin. Sorudaki Şekil I ve Şekil II de bunu göstermektedir.
12. Benzer Konular ve Ek Kaynaklar
- Üçgenin Benzerliği: 3-4-5 üçgeni, 6-8-10 üçgeni, 9-12-15 üçgeni gibi ölçeklenmiş üçgenler rampalarda sık sık karşımıza çıkar.
- Eğim ve Trigonometri İlişkisi: Lise müfredatında trigonometri (sinüs, kosinüs, tanjant) eğimin açısal yorumunu yapmak için kullanılır.
- Gerçek Hayattan Örnek: Yol mühendisliğinde veya mimarlıkta engelli rampaları tasarlanırken, benzer şekilde eğim hesapları yapılır.
13. Kapsamlı Sonuç
Derinlemesine incelediğimizde:
- Dikey yükseklik: 24 cm (4 kitap × 6 cm).
- İlk eğim: \frac{4}{3}, yani 4 birim dikey için 3 birim yatay. 24 cm dikeye karşılık 18 cm yatay; birinci rampanın uzunluğu 30 cm.
- 14 cm kaydırma: Yatay 18 cm → 18 + 14 = 32 cm. Dikey hâlâ 24 cm.
- Yeni rampanın uzunluğu: \sqrt{24^2 + 32^2} = \sqrt{1600} = 40 \text{ cm}.
Bu hesap ve çıkarımlar bizi 40 cm sonucuna ulaştırır. Daha açık bir ifadeyle, Cevap: 40 cm (D şıkkı).
14. Kaynakça ve Referanslar
Aşağıdaki kaynaklar, hem Türkiye’de eğitim müfredatında hem de uluslararası standartlarda benzer konuları ele alan güvenilir referanslardır:
- MEB Ortaokul ve Lise Matematik Ders Kitapları – Geometri ve Üçgenler konuları.
- OpenStax College (Mathematics / Geometry) – Üçgenler ve Pisagor Teoremi üzerine temel kaynak.
- TÜBİTAK Popüler Bilim Yayınları – Geometriye giriş nitelikli kaynaklar.
- National Geographic – Merdiven ve rampa tasarımı ile ilgili belgesel niteliğinde içerikler.
Bu kaynaklar, konuyu daha da derinlemesine anlamak ve ek örneklerle pratik yapmak isteyen öğrencilere rehberlik edebilir.
15. Hepsi Bir Arada Özet
Aşağıya, tüm süreci bir bakışta gözler önüne seren kapsamlı bir özet ekliyoruz:
- Kitap Yüksekliği: Her kitap 6 cm, 4 kitap = 24 cm.
- İlk Eğim (4/3):
- 24 / x = 4/3 \implies x = 18 cm.
- Birinci rampanın uzunluğu = \sqrt{24^2 + 18^2} = 30 cm.
- Daha Az Dik Yapma: 14 cm yatay kaydırma → Yatay = 18 + 14 = 32 cm.
- İkinci Rampanın Uzunluğu: \sqrt{24^2 + 32^2} = 40 cm.
- Son Cevap: 40 cm (D).
Bu tip problemleri çözmeye alıştığınızda, geometri ve basit trigonometri kavramlarının ne kadar faydalı olduğunu göreceksiniz. Ayrıca gerçek hayatta basit rampalardan karmaşık yol projelerine kadar sayısız uygulama alanı bulacaksınız.
16. Soru ve Cevap Metninin Nihai Şekli
Soru:
Furkan 6 santimetre yüksekliğindeki özdeş dört kitabın Şekil I’deki gibi dizerek oyuncak arabası için eğimi 4/3 olan bir rampa hazırlamış fakat arabası rampayı tırmanamayınca levhayı ok yönünde 14 santimetre kaydırarak rampanın eğimini azaltmıştır. Şekil II’deki levha ile en üstteki kitabın uç noktaları değişmediğine göre Furkan’ın oluşturduğu ikinci rampanın uzunluğu kaç santimetredir?
Cevap:
- Birinci rampa için yükseklik 24 cm, eğim 4/3 olduğundan yatay mesafe 18 cm, rampanın uzunluğu 30 cm bulunur.
- Rampayı 14 cm kaydırdığımızda yeni yatay mesafe 32 cm olur. Dolayısıyla ikinci rampanın uzunluğu\sqrt{(24)^2 + (32)^2} = \sqrt{576 + 1024} = \sqrt{1600} = 40 \text{ cm}şeklinde hesaplanır.
Şıklar arasından doğru cevap D) 40 cm’dir.