Soru
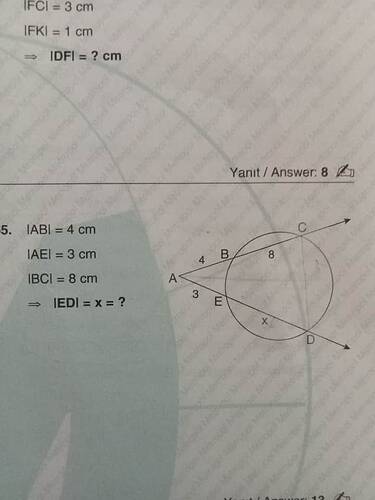
IABI = 4 cm, IAEI = 3 cm, IBCI = 8 cm ⇒ IEDI = x = ?
Cevap:
1. Adım: Problemin İncelenmesi
Yukarıdaki şekilde, A noktası çemberin dışındadır ve iki kesen çizilmektedir:
- Birinci kesen, A’dan başlayıp B ve ardından C noktalarından geçerek çemberi keser.
- İkinci kesen ise A’dan başlayıp E ve D noktalarından geçerek çemberi keser.
Bu tür sorular, dışarıdan çekilen iki kesen (Power of a Point) teoremiyle çözülür. Teoreme göre:
(\text{Dış kısım}) \times (\text{Tam kesen uzunluğu}) = (\text{Diğer dış kısım}) \times (\text{Diğer tam kesen uzunluğu})
2. Adım: Uzunlukları Tanımlama
• Birinci kesenin dış kısmı:
- AB = 4 cm
• Birinci kesenin tamamı (AC): - AC = AB + BC = 4 cm + 8 cm = 12 cm
• İkinci kesenin dış kısmı:
- AE = 3 cm
• İkinci kesenin tamamı (AD): - AD = AE + ED = 3 + x cm
3. Adım: Kesen-Kesen Kuvvet Teoreminin Uygulanması
Teoremi aşağıdaki gibi kuruyoruz:
(AB) \times (AC) = (AE) \times (AD)
Verilen değerlere göre:
4 \times 12 = 3 \times (3 + x)
4. Adım: Denklemin Çözümü
• Sol taraf:
4 × 12 = 48
• Sağ taraf:
3 × (3 + x) = 9 + 3x
Denklemi eşitleyip çözelim:
48 = 9 + 3x \implies 48 - 9 = 3x \implies 39 = 3x \implies x = 13
Dolayısıyla IEDI = 13 cm bulunur.
Özet Tablosu
| Bölüm | İşlem | Sonuç |
|---|---|---|
| 1. Kesen 1 Dış Kısmı | AB = 4 cm | 4 cm |
| 2. Kesen 1 Tam Uzunluk | AC = AB + BC = 4 + 8 | 12 cm |
| 3. Kesen 2 Dış Kısmı | AE = 3 cm | 3 cm |
| 4. Kesen 2 Tam Uzunluk | AD = AE + ED = 3 + x | (3 + x) cm |
| 5. Teorem Uygulaması | 4 × 12 = 3 × (3 + x) | 48 = 9 + 3x |
| 6. Denklemin Çözümü | 48 - 9 = 39 ⇒ 39 / 3 = x | 13 cm |
| Sonuç (IEDI) | x = | 13 cm |
Kısa Özet
Dışarıdan çekilen iki kesen teoremine göre, dış kısım ile kesenin tamamının çarpımı diğer kesendeki dış kısım ve kesenin tamamının çarpımına eşittir. Burada AB·AC = AE·AD denklemi kullanıldığında x = 13 cm elde edilir.