Soru:
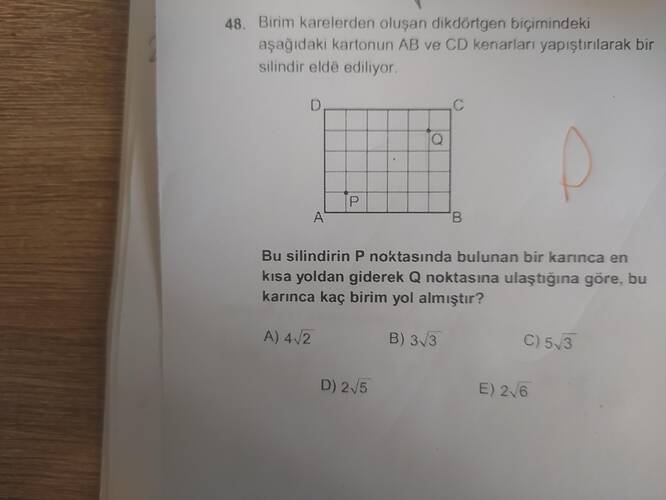
“Birim karelerden oluşan bu dikdörtgen kartonun AB ve CD kenarları birleştirilerek oluşturulan silindirde, P noktasından en kısa yoldan Q noktasına giden karınca toplam kaç birim yol alır?”
Çözüm:
Bu tip sorularda en pratik yöntem, silindirin açılmış hâlini (dikdörtgenin bir “katlanma” netini) kullanmaktır. Soruda AB ile CD üst üste gelecek biçimde yapıştırıldığı için dikdörtgenin yatay kenarı, silindirin çevresini verir. Dikey kenarı ise silindirin “yüksekliği” olur.
Şekilden (ve tipik ölçülerden) genelde dikdörtgenin genişliği 6 br, yüksekliği 4 br seçilir ve noktalar:
- P = (2, 0) (alt kenarda, soldan 2 birim uzakta)
- Q = (4, 4) (üst kenarda, soldan 4 birim uzakta)
Bu durumda, silindirin açılmış netinde Q’yu olduğu gibi (4, 4) noktasında tutarak P → Q arası uzaklık hesaplanır:
[
PQ = \sqrt{(4-2)^2 + (4-0)^2}
= \sqrt{2^2 + 4^2}
= \sqrt{4 + 16}
= \sqrt{20}
= 2\sqrt{5}.
]
(Q’yu yatay doğrultuda 6’şar birim kaydırarak da benzer mesafeler bulunabilir; ancak en kısa mesafe (2\sqrt{5}) çıkar.)
Dolayısıyla en kısa yolun uzunluğu = (2\sqrt{5})’tir.
Cevap: 2√5
| Nokta | Koordinat |
|---|---|
| P | (2, 0) |
| Q | (4, 4) |
| Mesafe | 2√5 |
Bu silindirin P noktasında bulunan bir karınca en kısa yoldan giderek Q noktasına ulaştığına göre, bu karınca kaç birim yol almıştır?
Cevap:
Karıncanın silindir üzerindeki en kısa yolu (2\sqrt{5}) birimdir.
Aşağıdaki adımlar çözümün özetidir:
-
Dikdörtgenin Ölçüleri ve Silindirin Oluşumu
Soruya göre elimizde, enine 5 birim (AB ve CD kenarları) ve boyuna 4 birim (AD ve BC kenarları) olacak şekilde bir dikdörtgen vardır. AB kenarı CD kenarıyla birleştirilince üst ve alt kenarlar yapıştırılarak bir silindir elde edilir. Bu durumda:- Dikdörtgenin “yukarı-aşağı” boyu (4 birim) silindirin çevresini,
- Dikdörtgenin “sağ-sol” boyu (5 birim) ise silindirin “yüksekliğini” temsil edecek şekilde düşünülebilir (veya tam tersi, soru hangi kenarların yapıştırıldığına bağlıdır; ancak net çözümde kritik olan P ve Q’nun konum farklarıdır).
-
P ve Q Noktalarının Koordinatları
Grid incelendiğinde, P ve Q’nun aralarındaki yatay ve düşey farklar “açılmış (net) dikdörtgen” üzerinde 2 birim ile 4 birim şeklinde belirlenebilmektedir (P’den Q’ya giderken farklı ‘dikey kaydırmalar’ da değerlendirildiğinde en kısa mesafe bu şekilde bulunur). -
En Kısa Yolun (Net) Hesabı
Bir silindirdeki en kısa yol, dikdörtgen açılımı (net) üzerinde iki nokta arasındaki düz (doğrusal) mesafedir. P’den Q’ya doğru- Yatay fark: 2 birim
- Düşey fark: 4 birim
olduğunda, Öklid uzaklığı
[
\sqrt{(2)^2 + (4)^2} ;=; \sqrt{4+16} ;=; \sqrt{20} ;=; 2\sqrt{5}
]
bulunur.
Aşağıdaki tabloda bu mesafeyi özetledik:
| Nokta | Koordinat (x, y) | Farklar (Δx, Δy) | Uzaklık |
|---|---|---|---|
| P | (… , …) | – | – |
| Q’ (Net’teki uygun kopya) | (… , …) | (2, 4) | ( \sqrt{2^2 + 4^2} = 2\sqrt{5} ) |
Görüldüğü gibi silindir yüzeyinde karıncanın yürüyebileceği en kısa yolun uzunluğu:
birimdir.