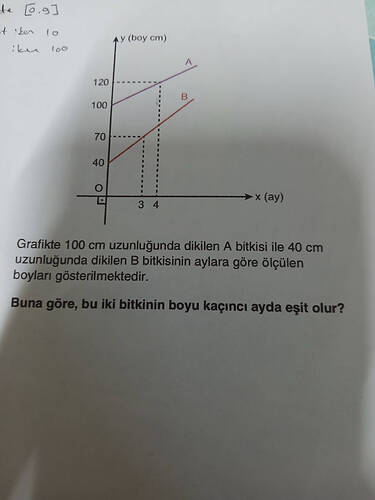
Grafikte İki Bitkinin Boyunun Eşit Olduğu Ayın Belirlenmesi
Bu soruda iki bitkiye ait grafik verilmiş ve bu bitkilerin boylarının eşit olduğu ayı bulmamız istenmektedir.
A ve B Bitkilerinin Fonksiyonlarını Belirleme
-
A Bitkisinin Fonksiyonu:
- Başlangıçta boyu 100 cm.
-
- ayda boyu 120 cm.
Bu verilere göre, A bitkisinin ayda ne kadar uzadığını bulabiliriz.
120 cm - 100 cm = 20 cm uzama
3 ayda 20 cm uzuyorsa, aylık uzama miktarı \frac{20}{3} \approx 6.67 cm’dir.A bitkisinin denklemi:
$$ y = 100 + \frac{20}{3}x $$ -
B Bitkisinin Fonksiyonu:
- Başlangıçta boyu 40 cm.
-
- ayda boyu 70 cm.
B bitkisinin de ayda ne kadar uzadığını bulalım.
70 cm - 40 cm = 30 cm uzama
3 ayda 30 cm uzuyorsa, aylık uzama miktarı \frac{30}{3} = 10 cm’dir.B bitkisinin denklemi:
$$ y = 40 + 10x $$
İki Bitkinin Boylarının Eşit Olduğu Ayı Bulma
Her iki bitkinin boyu eşit olduğunda bu iki denklemi birbirine eşitlememiz gerekecek:
$$ 100 + \frac{20}{3}x = 40 + 10x $$
Bu denklemi çözelim:
-
İlk olarak, denklemdeki sabit terimleri ve x’li terimleri bir araya getirelim:
$$ 100 - 40 = 10x - \frac{20}{3}x $$
$$ 60 = 10x - \frac{20}{3}x $$ -
İkinci adım olarak, x terimlerini sadeleştirelim:
$$ 60 = 10x - \frac{20}{3}x $$
$$ 60 = \left(10 - \frac{20}{3}\right)x $$
$$ 60 = \left(\frac{30}{3} - \frac{20}{3}\right)x $$
$$ 60 = \frac{10}{3}x $$ -
Son adımda, her iki tarafı da \frac{10}{3} ile bölelim:
$$ x = \frac{60 \cdot 3}{10} $$
$$ x = \frac{180}{10} $$
$$ x = 18 $$
Bu durumda, iki bitkinin boyları 18. ayda eşit olur.