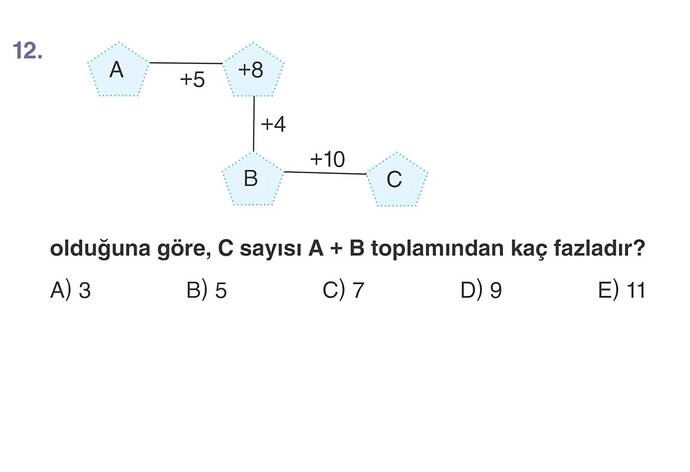
C sayısı A + B toplamından kaç fazladır?
Cevap:
Bu problemde, verilen artış sıralarını kullanarak her harfin değerini bulmalıyız.
İlk olarak, A, B ve C değerlerinin birbirleri ile olan ilişkisini göz önünde bulunduralım:
-
A değeri:
- A’nın değeri herhangi bir sayı olabilir, bu nedenle A’yı A olarak sabit tutalım.
-
B değeri:
- B, A’nın değerine +5 eklenerek bulunur.B = A + 5
- B, A’nın değerine +5 eklenerek bulunur.
-
B’nin tekrar hesaplanması:
-
B’nin değeri, A’ya +8 eklenerek bulunur.
B = A + 8 -
İlk durumda B’nin değeri:
B = A + 5 -
İkinci durumda B’nin değeri (“A + 5” ve “+4” ekleyerek):
B = (A + 5) + 4 = A + 9
Sonuç olarak, bu değerlerin çıkış noktalarına göre birbirlerini bulmalıyız.
-
-
C değeri:
- C, A’nın değerine +5, +8 ve +4 eklenmiş hali olarak bulunur.\text{C} = A + 5 + 8 + 4 + 10 = A + 27
- C, A’nın değerine +5, +8 ve +4 eklenmiş hali olarak bulunur.
Şimdi, C ile A + B toplamının farkını bulalım:
-
C’nin değeri:
C = A + 27 -
A + B toplamı:
A + B = A + (A + 8) = 2A + 8 -
C ile A + B toplamının farkı:
(A + 27) - (2A + 8) = A + 27 - 2A - 8= -A + 19
Bu nedenle, A ve B toplamına göre C sayısı, 19 fazladır.
Cevap:
Doğru seçenek:
D) 9