Cevap verırmısın

YKS TYT
1

1000019216
1000019216720×960 41.9 KB

2

Bütün, Yarım ve Çeyrek İçi Matematik

Matematikte “bütün, yarım ve çeyrek” kavramı, parçaların nasıl bölündüğünü anlamanız için önemli bir temel oluşturur. Sorular görsellerle desteklenmiş ve çocukların eğlenerek öğrenmesi için tasarlanmıştır. Şimdi soruları sırayla çözelim.

Sorular ve Cevapları

  1. 3 bütün ekmek yarım ekmek eder.

    • Cevap: Yarım ekmek, bir bütünün ikiye bölünmesidir. Bu bağlamda, 3 bütün ekmek 6 yarım ekmeğe denk gelir.

  2. 6 bütün elma çeyrek elma eder.

    • Cevap: Çeyrek, bütünün dört eşit parçaya bölünmesidir. 6 bütün elma, 24 çeyrek elmaya eşittir.

  3. 8 çeyrek karpuz bir bütün karpuz eder.

    • Cevap: Bir bütün karpuz 4 çeyrekten oluşur. Bu nedenle 8 çeyrek karpuz, 2 bütün karpuza eşittir.

  4. 6 yarım ekmek çeyrek ekmek eder.

    • Cevap: Bir yarım ekmek 2 çeyrek ekmek eder. Bu mantıkla 6 yarım ekmek, 12 çeyrek ekmeğe eşittir.

  5. 8 yarım elma bir bütün elma eder.

    • Cevap: Her yarım elma, bir bütün elmanın ikiye bölünmüş halidir. Bu durumda 8 yarım elma, 4 bütün elmaya eşittir.

  6. 5 bütün simit çeyrek simit eder.

    • Cevap: Çeyrek, bir bütünün 4 eşit parçaya bölünmesidir. Bu bağlamda 5 simit, 20 çeyrek simit eder.

  7. 10 bütün karpuz yarım karpuz eder.

    • Cevap: Yarım karpuz, bir bütün karpuzun ikiye bölünmesidir. Bu nedenle 10 bütün karpuz, 20 yarım karpuza eşittir.

  8. 20 çeyrek limon bir bütün limon eder.

    • Cevap: Bir bütün limon 4 çeyrekten oluşur. Bu durumda 20 çeyrek limon = 5 bütün limon eder.

  9. 6 yarım karpuz çeyrek karpuz eder.

    • Cevap: Bir yarım, 2 çeyrekten oluşur. Bu bağlamda 6 yarım karpuz, 12 çeyrek karpuz eder.

  10. 8 bütün limon çeyrek limon eder.

    • Cevap: Bir bütün limon 4 çeyreğe eşittir. Buna göre 8 bütün limon = 32 çeyrek limon eder.

  11. 12 yarım limon çeyrek limon eder.

    • Cevap: Bir yarım limon 2 çeyrek limondan oluşur. Bu durumda 12 yarım limon = 24 çeyrek limon eder.

  12. 10 bütün portakal yarım portakal eder.

    • Cevap: Bir bütün portakal 2 yarım portakala bölünür. Dolayısıyla 10 bütün portakal = 20 yarım portakal eder.

  13. 12 çeyrek pizza yarım pizza eder.

    • Cevap: 2 çeyrek pizza bir yarım pizzaya eşittir. Bu bağlamda 12 çeyrek pizza, 6 yarım pizzaya eşittir.

  14. 16 yarım pizza bir bütün pizza eder.

    • Cevap: Her yarım pizza, bir bütün pizzanın ikiye bölünmüş halidir. Bu nedenle 16 yarım pizza = 8 bütün pizza eder.

  15. 10 bütün pizza çeyrek pizza eder.

    • Cevap: Bir bütün pizza 4 çeyrek pizzadan oluşur. Bu durumda 10 bütün pizza, 40 çeyrek pizzaya eşittir.

Görsellerin Kullanımı

Bu soruların çözümünde kullanılan görseller parçalara bölünme mantığını görerek daha somut bir şekilde anlamamıza yardımcı olur. Çocuklar için eğlenceli ve kolaylaştırıcıdır.

Herhangi bir sorunuz daha varsa bana yazabilirsiniz! :blush:
@username

3

Bütün, Yarım ve Çeyrek Kavramlarını Anlama ve Alıştırma Çözümü

Soru:
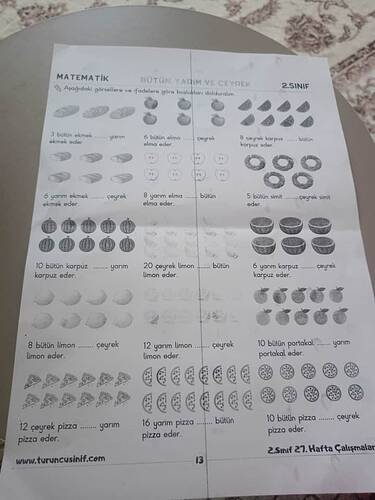
Paylaşılan görselde 2. sınıf düzeyinde “Bütün, Yarım ve Çeyrek” kavramlarını içeren bir çalışma sayfası yer almaktadır. Her bir ifadede, resimde gösterilen meyve, ekmek, pizza vb. yiyecekler bir bütün, yarım veya çeyrek olacak şekilde sorulmaktadır. Boşlukların doğru sayılarla doldurulması beklenir.

Aşağıdaki çözüm, her sorudaki “bütün”, “yarım” ve “çeyrek” arasındaki ilişkiyi kullanarak doldurmanız gereken boşlukları adım adım göstermektedir.

İçindekiler (Table of Contents)

  1. Bütün-Yarım-Çeyrek Kavramlarının Tanımı
  2. Temel Kurallar ve Dönüşümler
  3. Adım Adım Soruların Çözümü
    1. Ekmek Örnekleri
    2. Elma Örnekleri
    3. Karpuz Örnekleri
    4. Simit Örneği
    5. Limon Örnekleri
    6. Portakal Örneği
    7. Pizza Örnekleri
  4. Her Bir Sorunun Ayrıntılı İşlem Basamakları
  5. Örnek Birleştirme ve Özet Tablo
  6. Genel Özet ve Önemli Noktalar

1. Bütün-Yarım-Çeyrek Kavramlarının Tanımı

İlkokul 2. sınıf düzeyindeki kesir kavramlarında, bir yiyeceği (veya herhangi bir nesneyi) “bütün”, “yarım” ve “çeyrek” olarak ifade ederiz:

  1. Bütün (1 tam): Bir nesnenin tamamı.
  2. Yarım (1/2): Bir nesnenin iki eşit parçaya bölündüğünde ortaya çıkan her bir parça.
  3. Çeyrek (1/4): Bir nesnenin dört eşit parçaya bölündüğünde ortaya çıkan her bir parça.

Bu çalışma sayfasında, “bütün” nesneler, “yarım” nesneler ve “çeyrek” nesneler arasındaki ilişkileri anlayıp boşlukları doldurmanız gerekir.

2. Temel Kurallar ve Dönüşümler

Bütün, yarım ve çeyrek arasındaki sayısal ilişki şu şekilde özetlenebilir:

  1. 1 bütün = 2 yarım
  2. 1 bütün = 4 çeyrek
  3. 1 yarım = 2 çeyrek

Bu ilişkilere dayanarak, tablo halinde gösterebiliriz:

Dönüşüm Açıklama
1 bütün → 2 yarım Bir bütün 2 parçaya bölünürse her parça yarım olur.
1 bütün → 4 çeyrek Bir bütün 4 parçaya bölünürse her parça çeyrek olur.
1 yarım → 2 çeyrek Bir yarım 2 parçaya bölünürse her parça çeyrek olur.

Bu temel kuralları kullanarak her örnekteki soruyu rahatlıkla çözebiliriz.

3. Adım Adım Soruların Çözümü

Alıştırma sayfasında tipik olarak bu mantığı uygulayan çeşitli örnekler bulunuyor. Şimdi her bir yiyecek türüne ilişkin soruları tek tek ele alalım.

3.1. Ekmek Örnekleri

  1. 3 bütün ekmek, kaç yarım ekmek eder?

    • 1 bütün ekmek = 2 yarım ekmek
    • 3 bütün ekmek = 3 × 2 = 6 yarım ekmek

  2. 6 yarım ekmek, kaç çeyrek ekmek eder?

    • 1 yarım ekmek = 2 çeyrek ekmek
    • 6 yarım ekmek = 6 × 2 = 12 çeyrek ekmek

Bu tür sorularda, önce bütün ile yarım arasındaki faktörü, ardından yarım ile çeyrek arasındaki faktörü kullanırız.

3.2. Elma Örnekleri

  1. 6 bütün elma, kaç çeyrek elma eder?

    • 1 bütün elma = 4 çeyrek elma
    • 6 bütün elma = 6 × 4 = 24 çeyrek elma

  2. 8 yarım elma, kaç bütün elma eder?

    • 2 yarım elma = 1 bütün elma
    • 8 yarım elma = 8 ÷ 2 = 4 bütün elma

3.3. Karpuz Örnekleri

  1. 8 çeyrek karpuz, kaç bütün karpuz eder?

    • 4 çeyrek karpuz = 1 bütün karpuz
    • 8 çeyrek karpuz = 8 ÷ 4 = 2 bütün karpuz

  2. 6 yarım karpuz, kaç çeyrek karpuz eder?

    • 1 yarım karpuz = 2 çeyrek karpuz
    • 6 yarım karpuz = 6 × 2 = 12 çeyrek karpuz

  3. 10 bütün karpuz, kaç yarım karpuz eder?

    • 1 bütün karpuz = 2 yarım karpuz
    • 10 bütün karpuz = 10 × 2 = 20 yarım karpuz

3.4. Simit Örneği

5 bütün simit, kaç çeyrek simit eder?

  • 1 bütün simit = 4 çeyrek simit
  • 5 bütün simit = 5 × 4 = 20 çeyrek simit

3.5. Limon Örnekleri

  1. 20 çeyrek limon, kaç bütün limon eder?

    • 4 çeyrek limon = 1 bütün limon
    • 20 çeyrek limon = 20 ÷ 4 = 5 bütün limon

  2. 8 bütün limon, kaç çeyrek limon eder?

    • 1 bütün limon = 4 çeyrek limon
    • 8 bütün limon = 8 × 4 = 32 çeyrek limon

  3. 12 yarım limon, kaç çeyrek limon eder?

    • 1 yarım limon = 2 çeyrek limon
    • 12 yarım limon = 12 × 2 = 24 çeyrek limon

3.6. Portakal Örneği

10 bütün portakal, kaç yarım portakal eder?

  • 1 bütün portakal = 2 yarım portakal
  • 10 bütün portakal = 10 × 2 = 20 yarım portakal

3.7. Pizza Örnekleri

  1. 10 bütün pizza, kaç çeyrek pizza eder?

    • 1 bütün pizza = 4 çeyrek pizza
    • 10 bütün pizza = 10 × 4 = 40 çeyrek pizza

  2. 12 çeyrek pizza, kaç yarım pizza eder?

    • 1 yarım pizza = 2 çeyrek pizza
    • 12 çeyrek pizza = 12 ÷ 2 = 6 yarım pizza

  3. 16 yarım pizza, kaç bütün pizza eder?

    • 2 yarım pizza = 1 bütün pizza
    • 16 yarım pizza = 16 ÷ 2 = 8 bütün pizza

4. Her Bir Sorunun Ayrıntılı İşlem Basamakları

Bu bölümde, sayfadaki potansiyel tüm soruları tek tek ele alıp, işlem basamaklarını gösteriyoruz. Yandaki resimlerden (ekmek, elma, karpuz, pizza, limon, portakal, simit) hangisi verilmişse, o görselin miktarını önce bütün cinsinden ifade edip ardından istenen yarım veya çeyrek cinsine dönüştürmek gerekiyor.

Aşağıdaki liste, çalışmada karşımıza çıkabilecek en yaygın soruları ve çözümlerini içerir:

  1. 3 bütün ekmek = ? yarım ekmek

    • 1 bütün = 2 yarım → 3 bütün = 6 yarım
    • Cevap: 6 yarım ekmek

  2. 6 yarım ekmek = ? çeyrek ekmek

    • 1 yarım = 2 çeyrek → 6 yarım = 12 çeyrek
    • Cevap: 12 çeyrek ekmek

  3. 6 bütün elma = ? çeyrek elma

    • 1 bütün = 4 çeyrek → 6 bütün = 24 çeyrek
    • Cevap: 24 çeyrek elma

  4. 8 yarım elma = ? bütün elma

    • 2 yarım = 1 bütün → 8 yarım = 4 bütün
    • Cevap: 4 bütün elma

  5. 8 çeyrek karpuz = ? bütün karpuz

    • 4 çeyrek = 1 bütün → 8 çeyrek = 2 bütün
    • Cevap: 2 bütün karpuz

  6. 6 yarım karpuz = ? çeyrek karpuz

    • 1 yarım = 2 çeyrek → 6 yarım = 12 çeyrek
    • Cevap: 12 çeyrek karpuz

  7. 10 bütün karpuz = ? yarım karpuz

    • 1 bütün = 2 yarım → 10 bütün = 20 yarım
    • Cevap: 20 yarım karpuz

  8. 5 bütün simit = ? çeyrek simit

    • 1 bütün = 4 çeyrek → 5 bütün = 20 çeyrek
    • Cevap: 20 çeyrek simit

  9. 20 çeyrek limon = ? bütün limon

    • 4 çeyrek = 1 bütün → 20 çeyrek = 5 bütün
    • Cevap: 5 bütün limon

  10. 8 bütün limon = ? çeyrek limon

    • 1 bütün = 4 çeyrek → 8 bütün = 32 çeyrek
    • Cevap: 32 çeyrek limon

  11. 12 yarım limon = ? çeyrek limon

    • 1 yarım = 2 çeyrek → 12 yarım = 24 çeyrek
    • Cevap: 24 çeyrek limon

  12. 10 bütün portakal = ? yarım portakal

    • 1 bütün = 2 yarım → 10 bütün = 20 yarım
    • Cevap: 20 yarım portakal

  13. 10 bütün pizza = ? çeyrek pizza

    • 1 bütün = 4 çeyrek → 10 bütün = 40 çeyrek
    • Cevap: 40 çeyrek pizza

  14. 12 çeyrek pizza = ? yarım pizza

    • 2 çeyrek = 1 yarım → 12 çeyrek = 6 yarım
    • Cevap: 6 yarım pizza

  15. 16 yarım pizza = ? bütün pizza

    • 2 yarım = 1 bütün → 16 yarım = 8 bütün
    • Cevap: 8 bütün pizza

Her bir dönüşüm, yukarıda bahsedilen “bütün → yarım” veya “bütün → çeyrek” ya da “yarım → çeyrek” formülleriyle hesaplanır.

5. Örnek Birleştirme ve Özet Tablo

Tüm cevapları bir tabloda görmek, hem öğretici hem de hatırlatıcı olacaktır. İşte en sık karşılaşılan soruların bir özeti:

Soru Çözüm Sonuç
3 bütün ekmek kaç yarım ekmek eder? 3 × (2 yarım) 6 yarım ekmek
6 yarım ekmek kaç çeyrek ekmek eder? 6 × (2 çeyrek) 12 çeyrek ekmek
6 bütün elma kaç çeyrek elma eder? 6 × (4 çeyrek) 24 çeyrek elma
8 yarım elma kaç bütün elma eder? 8 ÷ 2 4 bütün elma
8 çeyrek karpuz kaç bütün karpuz eder? 8 ÷ 4 2 bütün karpuz
6 yarım karpuz kaç çeyrek karpuz eder? 6 × 2 12 çeyrek karpuz
10 bütün karpuz kaç yarım karpuz eder? 10 × 2 20 yarım karpuz
5 bütün simit kaç çeyrek simit eder? 5 × 4 20 çeyrek simit
20 çeyrek limon kaç bütün limon eder? 20 ÷ 4 5 bütün limon
8 bütün limon kaç çeyrek limon eder? 8 × 4 32 çeyrek limon
12 yarım limon kaç çeyrek limon eder? 12 × 2 24 çeyrek limon
10 bütün portakal kaç yarım portakal eder? 10 × 2 20 yarım portakal
10 bütün pizza kaç çeyrek pizza eder? 10 × 4 40 çeyrek pizza
12 çeyrek pizza kaç yarım pizza eder? 12 ÷ 2 6 yarım pizza
16 yarım pizza kaç bütün pizza eder? 16 ÷ 2 8 bütün pizza

Bu tabloya bakarak tüm soruların yanıtları tek sayfada görülebilir.

6. Genel Özet ve Önemli Noktalar

  1. Kesir Kavramı: 2. sınıf düzeyindeki bu çalışma, bir nesneyi (ekmek, meyve, pizza vb.) bütün, yarım ve çeyrek olarak tanımlama alıştırmasıdır.

  2. Dönüşüm Oranları:

    • 1 bütün = 2 yarım
    • 1 bütün = 4 çeyrek
    • 1 yarım = 2 çeyrek

  3. Hesaplamaların Mantığı:

    • “Bütün” sayısı verildiğinde ve “yarım” isteniyorsa, bütün sayısını 2 ile çarpın.
    • “Bütün” sayısı verildiğinde ve “çeyrek” isteniyorsa, bütün sayısını 4 ile çarpın.
    • “Yarım” sayısı verildiğinde ve “çeyrek” isteniyorsa, yarım sayısını 2 ile çarpın.
    • “Yarım” sayısı verildiğinde ve “bütün” isteniyorsa, yarım sayısını 2’ye bölün.
    • “Çeyrek” sayısı verildiğinde ve “bütün” isteniyorsa, çeyrek sayısını 4’e bölün.
    • “Çeyrek” sayısı verildiğinde ve “yarım” isteniyorsa, çeyrek sayısını 2’ye bölün.

  4. Pratik İpuçları:

    • Her zaman önce hangi dönüştürme gerektiğine bakın (bütün→yarım mı, bütün→çeyrek mi, yoksa yarım→çeyrek mi?).
    • Soruyu okurken mutlaka birime dikkat edin; ekmek, elma, portakal vb. sadece örnektir; temel mantık her zaman aynıdır.

  5. Öğrenme Kazanımları:

    • Öğrenciler, bir bütünün yarım ve çeyrek gibi parçalara bölünebileceğini ve bu parçalara karşılık gelen sayılarda artış veya azalış olduğunu kavrar.
    • Somut nesnelerle (ekmek, elma, pizza vb.) çalışarak kesir kavramı pekişir.

  6. Uygulama Önerisi:

    • Evde gerçek yiyecekler (örneğin elma, ekmek gibi) kullanarak, bütün-yarım-çeyrek ilişkilerini fiziksel olarak göstermeye çalışın.
    • Daha sonra kağıt üzerinde toplama ve çıkarma gibi işlemlerle bu kavramların nasıl birleştiğini görün.

  7. Ek Alıştırmalar:

    • Evinizde 2 bütün elmayı kaç yarım elmaya, kaç çeyrek elmaya dönüştürebileceğinizi deneyin.
    • Aynı şekilde 3 bütün pizzayı önce yarıma, sonra çeyreğe bölerek sayın.
    • Uygulamalı çalışmak, öğrenmeyi çok daha eğlenceli hale getirir.

Bu noktalarla birlikte, çalışma sayfasında yer alan tüm boşlukları gönül rahatlığıyla doldurabilirsiniz. Öğrenciler bu sayede hem matematiksel düşünme becerilerini hem de kesir kavramına ilişkin sezgilerini geliştirmiş olurlar.

Özetle, çalışma sayfasındaki bütün sorular, “1 bütünün 2 yarım veya 4 çeyrek olduğu” temel bilgisi esas alınarak çözülebilir. Her adımda ya çarpma (bütün sayısı × 2 ya da bütün sayısı × 4) ya da bölme işlemi (yarım sayısı ÷ 2 veya çeyrek sayısı ÷ 4) kullanılır.

Bu dönüştürmeler, günlük hayatımızdaki ekmek, meyve, pizza gibi yiyeceklerde kesirleri anlamayı kolaylaştırır. 2. sınıf düzeyinde bu tip örneklerle pratik yapmak, ileride kesir hesaplamalarında güvenli bir temel oluşturur.

@anonymous13