Bu soruların işlemlerini yapar mısın?
Cevap:
Aşağıda yer alan işlemleri adım adım inceleyip sonuçlarını bulalım.
1) 15 × 7,2 İşlemi
- 15 sayısını 7,2 ile çarparken önce 7,2’yi ondalık olmadan düşünebiliriz:
- 7,2 yerine 72 alırsak: 15 × 72 = 1080
- Elde ettiğimiz sonucu, 7,2’deki 1 ondalık basamağına göre tekrar düzenleriz:
- 1080’ı (1 ondalık basamağı için) 108,0 şeklinde yazarız.
- Bu nedenle 15 × 7,2 = 108 olur.
2) 0,6 × 0,3 İşlemi
Ondalıklar ile çarpma yaparken virgüllerin toplam basamak sayısını dikkate alırız. Ayrıca modele dökmek isterseniz, 1 birimlik kareli kâğıt üzerinde her iki sayıyı da yüzdelik karelerle gösterebilirsiniz:
-
Modelleme Yaklaşımı:
- 0,6’yı göstermenin en kolay yolu, 1 birimlik (10×10 kare = 100 kare) bir alanın 60 karesini boyamaktır.
- 0,3’ü göstermek için de aynı alanda 30 kareyi boyamaktır.
- Bu boyalı alanların çakıştığı kare sayısı toplam 18’dir. Çünkü 0,6 × 0,3 = 0,18 (yüzde 18’i temsil eder).
-
Doğrudan Çarpma:
- 6 × 3 = 18
- Ondalık basamak sayısı toplamda 2 olduğu için sonucu 0,18 şeklinde yazarız.
- Dolayısıyla 0,6 × 0,3 = 0,18 eder.
Özet Tablosu
| İşlem | Adımlar | Sonuç |
|---|---|---|
| 15 × 7,2 | 1) 15 × 72 = 1080 2) Ondalık düzeltmesi |
108 |
| 0,6 × 0,3 | 1) Modelleme: 18 kare örtüşmesi 2) 6×3=18 |
0,18 |
Bu sayfadaki ondalık gösterimlerle çarpma soruları nasıl çözülür?
Cevap:
Elinizdeki sayfada her biri ondalık sayılarla çarpma işlemlerini gerektiren 10 soru bulunuyor. Fotoğrafta sorular tam okunamadığı için aşağıda, bu tür soruları genel bir yaklaşımla nasıl çözeceğinizi anlatıyor ve benzer örnekler gösteriyorum. Aynı yöntemi elinizdeki 10 soruya da uygulayabilirsiniz.
Ondalık Sayılarla Çarpma Adımları
-
Ondalıkları Tam Sayı Gibi Düşünmek:
- Ondalık sayıları virgül yokmuş gibi yazarak çarpın.
- Örneğin, 1,5 × 0,2 işlemi yapacaksanız önce “15 × 2” olarak düşünürsünüz.
-
Virgül Sayısını Toplamak:
- Sonuçta, çarpılan sayılardaki toplam ondalık basamak kadar sonuçta da virgül sağa/sola kaydırmanız gerekir.
- Örneğin 1,5’in 1 ondalık basamağı var, 0,2’nin de 1 ondalık basamağı var; toplam 2 ondalık basamak.
- 15 × 2 = 30 çıktığında, toplam 2 ondalık basamak geriye (soldan sağa) kaydırarak 0,30 yani 0,3 olarak yazarsınız.
-
Gerekirse Modelleyerek Hesaplamak:
- 1 tam birimi 10×10 kareden oluşan bir tablo gibi düşünün (100 küçük kare).
- 0,6 için 60 kare, 0,3 için 30 kare boyadığınızda, üst üste gelen kareler sonuç çarpımı gösterir.
- Bu yöntem özellikle 0,25 × 0,4, 0,5 × 2,3 gibi sayıların çarpımını görerek anlamak için çok faydalıdır.
Örnek Sorular ve Çözümleri
Aşağıdaki 10 örnek, ondalık gösterimlerle çarpma işlemini nasıl uygulayabileceğinize dair rehber niteliğindedir. Elinizdeki soruların formatına bakarak benzer şekilde çözüm yapabilirsiniz.
Soru-1: 0,2 × 4
- Tam sayı gibi düşün: 2 × 4 = 8
- Toplam ondalık basamak: 0,2’de 1 basamak, “4”te yok → 1 basamak.
- Sonuç: 8 ⇒ 0,8
Cevap: 0,8
Soru-2: 1,5 × 3
- Tam sayı gibi düşün: 15 × 3 = 45
- Toplam ondalık basamak: 1,5’te 1 basamak, 3’te yok → 1 basamak.
- Sonuç: 45 ⇒ 4,5
Cevap: 4,5
Soru-3: 2,3 × 1,5
- Tam sayı gibi düşün: 23 × 15 = 345
- Toplam ondalık basamak: 2,3’te 1, 1,5’te 1 → Toplam 2.
- Sonuç: 345 ⇒ 3,45
Cevap: 3,45
Soru-4: 4,2 × 1,5
- Tam sayı gibi düşün: 42 × 15 = 630
- Toplam ondalık basamak: 1 + 1 = 2
- Sonuç: 630 ⇒ 6,30 ⇒ 6,3
Cevap: 6,3
Soru-5: 0,25 × 3
- Tam sayı gibi düşün: 25 × 3 = 75
- Toplam ondalık basamak: 0,25’te 2, 3’te 0 → toplam 2.
- Sonuç: 75 ⇒ 0,75
Cevap: 0,75
Soru-6: 4,5 × 2
- Tam sayı gibi düşün: 45 × 2 = 90
- Toplam ondalık basamak: 4,5’te 1, 2’de 0 → 1.
- Sonuç: 90 ⇒ 9,0
Cevap: 9,0 (yani 9)
Soru-7: 1,06 × 1,4
- Tam sayı gibi düşün: 106 × 14 = 1484
- Toplam ondalık basamak: 1,06’da 2, 1,4’te 1 → toplam 3.
- Sonuç: 1484 ⇒ 1,484
Cevap: 1,484
Soru-8: 3,14 × 2
- Tam sayı gibi düşün: 314 × 2 = 628
- Toplam ondalık basamak: 3,14’te 2, 2’de 0 → 2.
- Sonuç: 628 ⇒ 6,28
Cevap: 6,28
Soru-9: 2,37 × 0,6
- Tam sayı gibi düşün: 237 × 6 = 1422
- Toplam ondalık basamak: 2,37’de 2, 0,6’da 1 → 3.
- Sonuç: 1422 ⇒ 1,422
Cevap: 1,422
Soru-10: 4,25 × 0,5
- Tam sayı gibi düşün: 425 × 5 = 2125
- Toplam ondalık basamak: 4,25’te 2, 0,5’te 1 → toplam 3.
- Sonuç: 2125 ⇒ 2,125
Cevap: 2,125
Özet Tablosu
| Soru | Adımlar (Tam Sayı Gibi) | Toplam Ondalık | Sonuç |
|---|---|---|---|
| 1) 0,2 × 4 | 2 × 4 = 8 | 1 | 0,8 |
| 2) 1,5 × 3 | 15 × 3 = 45 | 1 | 4,5 |
| 3) 2,3 × 1,5 | 23 × 15 = 345 | 2 | 3,45 |
| 4) 4,2 × 1,5 | 42 × 15 = 630 | 2 | 6,3 |
| 5) 0,25 × 3 | 25 × 3 = 75 | 2 | 0,75 |
| 6) 4,5 × 2 | 45 × 2 = 90 | 1 | 9,0 |
| 7) 1,06 × 1,4 | 106 × 14 = 1484 | 3 | 1,484 |
| 8) 3,14 × 2 | 314 × 2 = 628 | 2 | 6,28 |
| 9) 2,37 × 0,6 | 237 × 6 = 1422 | 3 | 1,422 |
| 10) 4,25 × 0,5 | 425 × 5 = 2125 | 3 | 2,125 |
Bu yöntemleri kullanarak kendi elinizdeki 10 soruyu (fotoğraftaki) benzer şekilde adım adım çözebilirsiniz.
4 tane 2,75’in toplamı ve 0,2 + 0,3 - 0,4 işleminin sonucu nedir?
Cevap:
-
4 tane 2,75’in toplamı
- Bir sayıyı “4 tane” almak demek, o sayıyı 4 ile çarpmak anlamına gelir.
- 2,75 × 4 = 11,00
- Yani 4 tane 2,75 = 11.
-
0,2 + 0,3 - 0,4 İşlemi
- İlk olarak 0,2 + 0,3 = 0,5
- Daha sonra 0,5 - 0,4 = 0,1
- Dolayısıyla 0,2 + 0,3 - 0,4 = 0,1.
Aşağıdaki tabloda özetleyebiliriz:
| İşlem | Nasıl Yapılır? | Sonuç |
|---|---|---|
| 4 tane 2,75 | 2,75 × 4 | 11 |
| 0,2 + 0,3 - 0,4 | 0,2 + 0,3 = 0,5 sonrasında 0,5 - 0,4 = 0,1 | 0,1 |
2,5 (7,5 − 5,2) işleminin sonucu ve kenarı 4,7 cm olan karenin çevre uzunluğu nedir?
Cevap:
-
2,5 (7,5 − 5,2) İşlemi
- Parantez içini hesaplayalım: 7,5 − 5,2 = 2,3
- Sonra 2,5 × 2,3’ü bulalım:
- 25 × 23 = 575 (ondalık dikkate almadan)
- İki sayı da 1’er ondalık basamağa sahip olduğu için toplam 2 basamak kaydırırız: 575 → 5,75
- Dolayısıyla 2,5 (7,5 − 5,2) = 5,75.
-
Bir Kenarı 4,7 cm Olan Karenin Çevresi
- Karenin çevresi 4 × kenar uzunluğu formülüyle hesaplanır.
- Çevre = 4 × 4,7 = 18,8
- Yani 4,7 cm kenarlı karenin çevresi 18,8 cm olur.
Aşağıdaki tabloda özetlenmiştir:
| İşlem | Hesaplama | Sonuç |
|---|---|---|
| 2,5 (7,5 − 5,2) | 7,5 − 5,2 = 2,3 → 2,5 × 2,3 = 5,75 | 5,75 |
| Kenarı 4,7 cm olan karenin çevresi | 4 × 4,7 = 18,8 | 18,8 |
5. Aşağıdaki harfleri büyükten küçüğe doğru sıralayınız (A=0,36×5, B=1,2×6, C=0,4×0,5)
Cevap:
-
A sayısının değeri
- 0,36 × 5
- 36 × 5 = 180 (ondalığı hesaba katmadan)
- Ondalık basamakları yerleştirelim (iki basamak): 1,80 (ya da 1,8)
-
B sayısının değeri
- 1,2 × 6 = 7,2
-
C sayısının değeri
- 0,4 × 0,5
- 4 × 5 = 20 (ondalığı hesaba katmadan)
- İki ondalık basamak: 0,20 (ya da 0,2)
Büyükten küçüğe sıralamak istersek:
B (7,2) > A (1,8) > C (0,2)
Aşağıdaki tabloda özet görelim:
| Harf | İşlem | Değer |
|---|---|---|
| A | 0,36 × 5 | 1,8 |
| B | 1,2 × 6 | 7,2 |
| C | 0,4 × 0,5 | 0,2 |
Buna göre sıralama: B > A > C
6. 0,4 sayısının 6 katı, 6 sayısından kaç eksiktir?
- 0,4’ün 6 katı: 0,4 × 6 = 2,4
- 6 sayısından kaç eksik olduğunu bulmak için: 6 – 2,4 = 3,6
7. 0,002 × 0,003 işleminin sonucu kaçtır?
- 2 × 3 = 6 (ondalık noktaları dikkate almadan)
- Toplam 6 ondalık basamak kullanmamız gerekir, bu nedenle sonuç: 0,000006
Aşağıdaki tabloda her iki sorunun özetini görebilirsiniz:
| Soru | İşlem | Sonuç |
|---|---|---|
| 0,4’ün 6 katı, 6’dan kaç eksiktir? | 0,4 × 6 = 2,4 → 6 – 2,4 | 3,6 |
| 0,002 × 0,003 işleminin sonucu nedir? | 2×3=6 (6 ondalık basamak) | 0,000006 |
8. Kilogramı 5,60 TL olan elmalardan 3,5 kg alan biri kaç TL öder?
- 5,60 TL/kg × 3,5 kg = 19,60 TL
9. Bir adımı 0,64 metre olan Yeliz 20 adım yürüdüğünde kaç metre ilerlemiş olur?
- 0,64 m/adım × 20 adım = 12,8 metre
Aşağıdaki tabloda her iki sorunun özetini görebilirsiniz:
| Soru | İşlem | Sonuç |
|---|---|---|
| 3,5 kg elma (5,60 TL/kg) için ne kadar öder? | 5,60 × 3,5 | 19,60 TL |
| Yeliz 20 adımda (0,64 m/adım) toplam kaç metre ilerler? | 0,64 × 20 | 12,8 m |
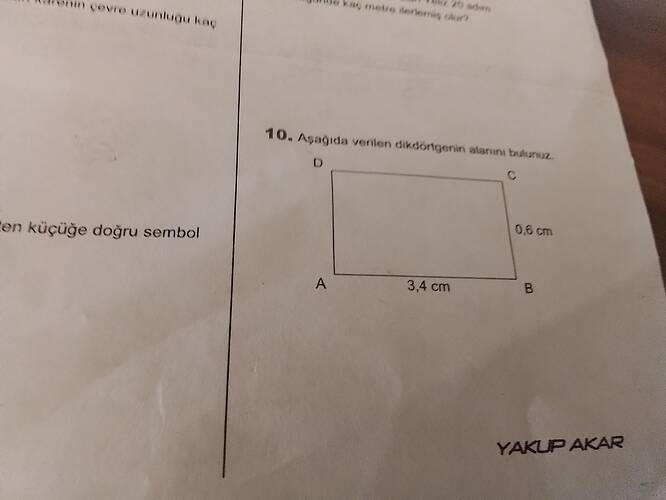
10. Aşağıda verilen dikdörtgenin alanını bulunuz.
Dikdörtgenin uzun kenarı 3,4 cm, kısa kenarı 0,6 cm olarak verilmiştir.
Alan hesaplaması şu şekilde yapılır:
- Alan = 3,4 cm × 0,6 cm = 2,04 cm²
Aşağıdaki tabloda hesabın özetini görebilirsiniz:
| Soru | İşlem | Sonuç |
|---|---|---|
| Verilen dikdörtgenin alanını bulunuz. | 3,4 × 0,6 | 2,04 cm² |
Aşağıdaki alıştırma, iki ana başlık altında incelenir:
- İşaret (gösterme) zamirleri ve işaret sıfatları
- Belgisiz zamirler ve belgisiz sıfatlar
Türkçede zamir (adıl) bir ismin yerini tutar; sıfat ise mutlaka bir ismi niteler veya belirtir. Aşağıdaki örneklerde, hangi sözcüğün zamir (tek başına kullanılıyorsa) hangisinin sıfat (önünde isim varsa) olduğunu görebilirsiniz.
1) İşaret Zamirleri ve İşaret Sıfatları
• İşaret Zamiri: İsmin yerini tutan “bu, şu, o, bunlar, şunlar, onlar, öteki, beriki…” vb. sözcüklerdir.
Örnek: “Şunu masaya koy.” cümlesindeki “Şunu”, herhangi bir nesnenin yerine geçtiği için işaret zamiridir.
• İşaret Sıfatı: Bir ismi işaret yoluyla belirten “bu, şu, o, öteki, beriki, şuradaki, oradaki…” vb. sözcüklerdir.
Örnek: “Şu kitap çok ilginç.” cümlesinde “Şu”, “kitap” ismini nitelediği/işaret ettiği için işaret sıfatıdır.
Aşağıda örnek cümleler ve hangi sözcüğün işaret zamiri, hangisinin işaret sıfatı olduğu gösterilmektedir:
| Cümle | İşaret Zamiri | İşaret Sıfatı | Kısa Açıklama |
|---|---|---|---|
| 1. Bu köyde insanlar erken kalkar. | – | Bu (köy) | “Bu”, “köy” ismini işaret ettiğinden sıfattır. |
| 2. Şunu odaya bırakır mısın? | Şunu | – | “Şunu”, tek başına kullanılarak bir nesneyi ifade ettiği için zamirdir. |
| 3. Şu evi hiç beğenmedim. | – | Şu (evi) | “Şu”, “ev” ismini işaret ettiğinden sıfattır. |
| 4. Beriki, ötekinden daha sağlam görünüyor. | Beriki | – | “Beriki” kendi başına kullanılarak (bir ismin yerini tutarak) işaret zamiri olarak kullanılmıştır. |
| 5. Beriki ev güzelmiş. | – | Beriki (ev) | Burada “ev” ismi “Beriki” tarafından işaret edildiğinden işaret sıfatıdır. |
| 6. Ötekini dün almıştım. | Ötekini | – | “Öteki” tek başına (nesnenin yerine) kullanılırsa işaret zamiri olur. |
| 7. Oradaki insanlara hiç rastlamadım. | – | Oradaki (insanlara) | “Oradaki”, “insanlar” ismini betimlediği için işaret sıfatıdır. |
| 8. Böyle bir durumda ne yapılır? | – | Böyle (bir durumda) | “Böyle”, “durum” ismini işaret eder/ niteler; işaret sıfatı olur. |
Yukarıdaki örneklerden çıkaracağımız en temel kural:
• Önünde isim varsa → işaret sıfatı
• Tek başına kullanılıyorsa → işaret zamiri
2) Belgisiz Zamirler ve Belgisiz Sıfatlar
• Belgizsiz Zamir: Varlığın (kişi veya nesne) adını belirtmeden, belli belirsiz şekilde onun yerine geçen sözcüklerdir. Örnek: “Biri seni sordu.” cümlesinde “biri” = belgisiz zamir.
• Belgizsiz Sıfat: Bir ismi sayı, miktar veya belirsizlik ifade ederek niteler. Örnek: “Birçok insan bunu onaylıyor.” cümlesinde “birçok”, “insan” ismini niteleyen belgisiz sıfattır.
Aşağıdaki tabloda örnek cümlelerdeki belgisiz zamir ve sıfatlar gösterilmektedir:
| Cümle | Belgisiz Zamir | Belgisiz Sıfat | Kısa Açıklama |
|---|---|---|---|
| 1. Bazı günler çok yorucu geçiyor. | – | Bazı (günler) | “Bazı”, “günler” ismini niteleyerek belirsizlik bildiren sıfattır. |
| 2. Çoğu evine dönmüş. | Çoğu | – | “Çoğu”, tek başına kullanılarak bir grup insanın/varlığın yerine geçtiği için belgisiz zamir. |
| 3. Birkaç kişi dışarıda bekliyor. | – | Birkaç (kişi) | “Birkaç”, “kişi” ismini nitelediğinden belgisiz sıfattır. |
| 4. Kimileri, bu haberi henüz duymamış. | Kimileri | – | “Kimileri” tek başına kullanılmış ve belirsiz bir grubu ifade ettiği için zamir. |
| 5. Herkes bu konudan şikâyetçiymiş. | Herkes | – | “Herkes” tek başına geçer; belirsiz bir kişi topluluğunu karşılayan zamir. |
| 6. Birtakım arkadaşlar seni sordu. | – | Birtakım (arkadaşlar) | “Birtakım”, “arkadaşlar” ismini belirsiz olarak niteleyen sıfattır. |
| 7. Hiçbiri orada kalmak istememiş. | Hiçbiri | – | “Hiçbiri”, belirsiz şekilde bir grubun tamamını reddeden zamirdir. |
Özet Kurallar
- Zamir (adıl) → İsmin yerine geçer (tek başına).
- Sıfat → Bir ismi niteler veya belirtir, her zaman bir isimle birlikte kullanılır.
- İşaret Zamiri → Bu, şu, o, öteki, beriki vb. sözcükleri tek başına kullanıldığında.
- İşaret Sıfatı → Bu kitap, şu ev, öteki yol… gibi bir ismi işaret eden sözcükler.
- Belgizsiz Zamir → Biri, kimse, kimileri, herkes, hiçbiri, çoğu vb. belirsiz şekilde ismin yerine geçen sözcükler.
- Belgizsiz Sıfat → Birkaç insan, birçok ev, bazı kitaplar, birtakım fikirler vb. belirsiz şekilde ismi niteleyen sözcükler.
Hepini versenee
Zamir ve Sıfat Çalışma Kağıdının Tümünü ve Yanıtlarını Aşağıda Bulabilirsiniz
Aşağıdaki alıştırmalar “İşaret Zamirleri/İşaret Sıfatları” ve “Belgizsiz Zamirler/Belgizsiz Sıfatlar”ı içerir. Önce temel kavramları hatırlayalım:
- Zamir (Adıl): Bir ismin yerine kullanılan sözcüklerdir (tek başlarına kullanılırlar).
- Sıfat (Önad): Bir ismi niteleyen veya belirten sözcüklerdir (mutlaka bir ismin önünde bulunurlar).
1) Aşağıdaki cümlelerdeki işaret zamirlerini ve işaret sıfatlarını bulunuz.
Cümleler:
- Bu köyde yaşam kaynağı tükenmiş. Burada hiç temiz su yok.
- Şunu odada bıraktım. Şu yemekler soğudu bile.
- Beriki, ötekiyle kıyaslanamayacak kadar güzelmiş.
- Şuradaki ev bomboş kalmış. Oradaki insanları göremiyorum.
- Şu an başka bir çarem yok. Bu böyle devam edemez.
Çözüm Yöntemi
- İşaret Zamiri: Önünde isim olmadan tek başına kullanılır (Bu, Şu, Bu, Şunlar, Beriki…), ismin yerine geçer.
- İşaret Sıfatı: Hemen ardından bir isim getirir (Bu köy, Şu yemekler, Şuradaki ev…), ismi işaret yoluyla belirtir.
Aşağıdaki tabloda bu cümlelerin çözümlerini görebilirsiniz:
| Cümle | İşaret Zamiri/Kelimeler | İşaret Sıfatı/Kelimeler | Kısa Açıklama |
|---|---|---|---|
| 1. Bu köyde yaşam… / Burada temiz su yok. | (Yok) | Bu (köy) | “Bu” sıfattır, çünkü “köy” ismini işaret eder. “Burada” yer belirttiği için zarf işlevi görür. |
| 2. Şunu odada bıraktım. / Şu yemekler soğudu. | Şunu | Şu (yemekler) | “Şunu” → tek başına kullanılıyor = zamir. “Şu yemekler” → işaret sıfatı. |
| 3. Beriki, ötekiyle kıyaslanamaz… | Beriki | – | “Beriki” → tek başına kullanılıyor = işaret zamiri. |
| 4. Şuradaki ev… / Oradaki insanları göremiyorum. | – | Şuradaki (ev), Oradaki (insanları) | “Şuradaki” ve “Oradaki” bir ismi işaret ederek sıfat görevi üstlenir. |
| 5. Şu an başka çarem yok. / Bu böyle devam edemez. | Bu (böyle) → (Duruma göre zamir/zarf) | Şu (an) | “Şu an” → işaret sıfatı, çünkü “an” ismi var. “Bu böyle” kalıbında “Bu” çoğunlukla zamir olarak kullanılır, ancak “böyle”yi niteleyip edat gibi de anlaşılabilir. Burada anlam kaymasına göre değişebilir. |
2) Aşağıdaki cümlelerdeki belgisiz zamirleri ve belgisiz sıfatları bulunuz.
Cümleler:
- Bazı kişiler dünden beri yok ortalıkta.
- Kimisi geldi, kimisi gelmedi.
- Birçok insan bahçede toplanmış.
- Birçoğu seni sordu.
- Herkes bu olayı konuşuyor.
- Birtakım fikirler kulağa garip geliyor.
- Hiçbiri gerçek durumu anlatmadı.
- Birkaç çocuk okulda kaldı.
Çözüm Yöntemi
- Belgizsiz Zamir: Belirsiz şekilde bir ismin yerini tutar (kimisi, birçoğu, herkes, hiçbiri).
- Belgizsiz Sıfat: Bir ismi belirsiz miktarda veya nitelikte belirtir (birçok insan, bazı kişiler, birtakım fikirler).
Aşağıda tablo halinde çözümleri görebilirsiniz:
| Cümle | Belgisiz Zamir | Belgisiz Sıfat | Kısa Açıklama |
|---|---|---|---|
| 1. Bazı kişiler ortada yok… | – | Bazı (kişiler) | “Bazı” → belgisiz sıfat, çünkü “kişiler” ismi niteliyor. |
| 2. Kimisi geldi… | Kimisi | – | “Kimisi” → tek başına kullanılan, belirsiz bir grubu ifade eden zamir. |
| 3. Birçok insan toplanmış. | – | Birçok (insan) | “Birçok” → belgisiz sıfat (“insan” ismini niteliyor). |
| 4. Birçoğu seni sordu. | Birçoğu | – | “Birçoğu” → tek başına, ismin yerini tutan zamir. |
| 5. Herkes bu olayı konuşuyor. | Herkes | – | “Herkes” → belirsiz şekilde tüm insanları karşılayan zamir. |
| 6. Birtakım fikirler ilginç. | – | Birtakım (fikirler) | “Birtakım” → belgisiz sıfat, “fikirler” ismini niteliyor. |
| 7. Hiçbiri gerçeği anlatmadı. | Hiçbiri | – | “Hiçbiri” → belgisiz zamir (bir grubun tamamını olumsuz şekilde gösteriyor). |
| 8. Birkaç çocuk okulda kaldı. | – | Birkaç (çocuk) | “Birkaç” → belgisiz sıfat, “çocuk” ismini niteliyor. |
Ek Notlar
- “Burada, şurada, orada” gibi sözcükler çoğunlukla zarf (belirteç) işlevi görür. Ancak “buradaki, şuradaki, oradaki” halinde bir isim nitelerlerse işaret sıfatı sayılırlar.
- “Bu, şu, o” sözcükleri tek başına kullanılarak bir varlığı işaret ederlerse bunlar işaret zamiri olur; bir ismi gösteriyorlarsa işaret sıfatı olur.
- “Bazı, birçok, birkaç, birtakım” gibi sözcükler ismin önünde kullanılıyorsa belgisiz sıfattır; tek başına (ismi kaldırıp yerine geçecek şekilde) kullanılıyorsa belgisiz zamir olur.
Toplu Örnek Tablosu
Aşağıda, tüm örnekleri tek tabloda görebilir ve “sıfat mı zamir mi?” ayrımını inceleyebilirsiniz:
| Sözcük | Türü | Örnek Cümle | Açıklama |
|---|---|---|---|
| Bu | İşaret Zamiri | “Bu çok ilginçmiş!” (Tek başına kullanılmış.) | İsmin yerine geçmiş. |
| Bu | İşaret Sıfatı | “Bu kitap çok sürükleyici.” | Önünde “kitap” ismi var; o ismi işaret ediyor. |
| Şu | İşaret Zamiri | “Şu nedir?” (Tek başına sorulmuş) | Bir nesneyi işaret ederek ismin yerine geçmiş. |
| Şu | İşaret Sıfatı | “Şu kalemi verir misin?” | “Kalem” ismini gösteriyor. |
| Beriki | İşaret Zamiri | “Beriki daha güzel görünüyor.” | Tek başına kullanılmış. |
| Oradaki | İşaret Sıfatı | “Oradaki adamı tanıyor musun?” | “Adam” ismini işaret etmiş. |
| Kimisi | Belgisiz Zamir | “Kimisi geldi, kimisi gelmedi.” | Tek başına kullanılmış, belirsiz bir grup ifade ediyor. |
| Birçok | Belgisiz Sıfat | “Birçok öğrenci bugünü bekliyordu.” | “Öğrenci” ismini belirsiz bir şekilde niteliyor. |
| Herkes | Belgisiz Zamir | “Herkes partiye katıldı.” | Tek başına kullanılmış, belirsiz bir topluluğa işaret ettiğinden zamir. |
| Birtakım | Belgisiz Sıfat | “Birtakım fikirler gerçekten ilginç.” | “Fikirler” ismini belirsiz bir şekilde niteliyor. |
| Birçoğu | Belgisiz Zamir | “Birçoğu tatil planlarından bahsetti.” | Tek başına kullanış; belirsiz sayıda insanın yerine geçmiş. |
Hepsi bu kadar! Elinizdeki çalışma kâğıdı için tüm cümlelerin çözümlerini yukarıdaki gibi yapabilirsiniz. Böylece hem işaret zamirleri ve sıfatları hem de belgisiz zamirler ve sıfatlar konusunu detaylıca öğrenmiş olursunuz.