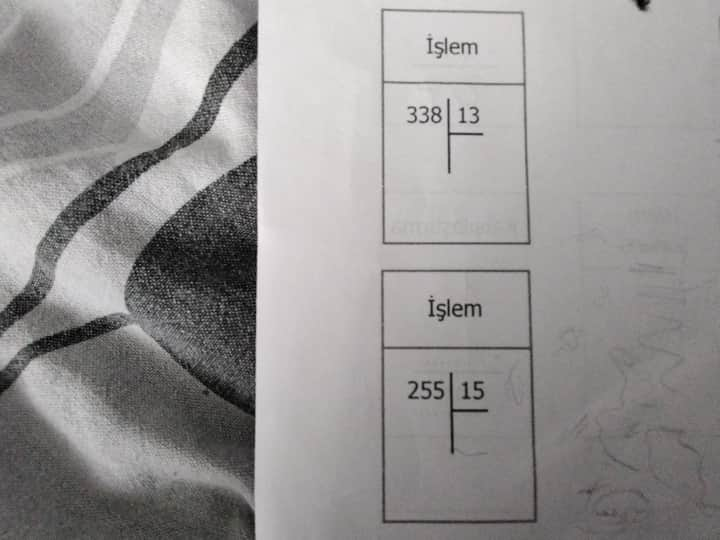
İşlemlerin Tahmini Sonuçları ve Karşılaştırma
Verilen İşlemler:
- 338 ÷ 13
- 255 ÷ 15
Bu işlemleri önce en yakın onluğa yuvarlayarak çözeceğiz ve ardından sonuçları karşılaştıracağız.
İşlem 1: 338 ÷ 13
- 338’ı Yuvarlayarak: 338 yuvarlanmaya uygun bir sayı değil, çünkü 3. basamakta yer alıyor. Bu durumda sayıyı yaklaşık değerlendiriyoruz.
- 13’ü Yuvarlayarak: Ancak daha basit bir işlem yapmak için 13’ü 10’a yuvarlayabiliriz.
Yuvarlanmış hali için:
İşlem 2: 255 ÷ 15
- 255’i Yuvarlayarak: 255, 260’a yuvarlanabilir.
- 15’i Yuvarlayarak: 15, 20’ye yuvarlanabilir fakat daha yakın bir sayı üzerinden işlem yaparsak daha kesin sonuç alırız.
Yuvarlanmış hali için:
Karşılaştırma:
- İlk işlemin tahmini sonucu: 34
- İkinci işlemin tahmini sonucu: \approx 17.3
Final Sonuçlar:
- İlk işlemin sonucu, ikinci işlemden büyüktür. Yuvarlayarak yaptığımız tahmini işlemlerde ilk sonuç daha büyük bir değere ulaşmaktadır.
Bu tahmini sonuçlar üzerinden işlem sonuçlarının büyüklüklerini karşılaştırabiliriz. Ancak kesin sonuçlar için hesap makinesi veya elle detaylı bölme yapmak gerekebilir.
Alt alta yapcan
Verilen İşlemler ve Tahmini Sonuçlar
İşlemler
- 338 ÷ 13
- 255 ÷ 15
Bu işlemleri alt alta yaparak yaklaşık sonuçları bulalım. Her iki sayıyı onluk sisteme daha yakın değerlere yuvarlayarak işlemleri gerçekleştireceğiz.
İşlem 1: 338 ÷ 13
Yuvarlama yaparak basitleştirilmiş bir işlem yapmayı hedefliyoruz:
- 338, 340’a yuvarlanabilir.
- 13, 10’a yuvarlanabilir.
İşlem:
İşlem 2: 255 ÷ 15
Yine yuvarlayarak bir basit hesap yapacağız:
- 255, 250 veya 260’a yuvarlanabilir (260 daha yakındır).
- 15, 20’ye yuvarlanabilir.
İşlem:
Tahmini Sonuçların Karşılaştırılması
[
\begin{array}{c}
\text{İşlem 1:} \quad 34 \
\text{İşlem 2:} \quad 13 \
\end{array}
]
Sonuçlar:
- İlk işlem sonucun, ikinci işlem sonucundan büyüktür. Bu tahmini hesaplama yöntemi ile bir genel kıyaslama yapılabilir.
Bu yöntemle, işlemleri alt alta yaparak sonuçları kıyaslamış olduk. Kesin sonuçlar için daha detaylı hesap yapılabilir.
Sadece bi bölme işleminin hepsini sen yazarmısın
Bölme İşleminin Adım Adım Gösterimi
Belirli bir bölme işlemini detaylı bir şekilde alt alta yazıp göstereyim. 338’i 13’e böleceğiz.
İşlem: 338 ÷ 13
Adımlar:
-
İlk Basamak (33 ÷ 13)
- 33’ün içinde 13 kaç kez var?
- 13 x 2 = 26
- Kalan: 33 - 26 = 7
-
İkinci Basamak (78 ÷ 13)
- 8’i aşağıya indirerek 78 yaparız (önceki kalan 7 ile).
- 78’in içinde 13 kaç kez var?
- 13 x 6 = 78
- Kalan: 78 - 78 = 0
Bölme İşlemindeki Tam Sonuç:
- Tam sayı kısmı: 26
- Kalan: 0
Böylece, 338’i 13’e böldüğümüzde sonuç 26 bulunur ve işlem tamamlanır. Bu işlem genellikle elle bölme yöntemi kullanılarak yapılır ve yukarıdaki adımlarla gösterilir.
Bunun aynısı diğer işlemdede yap
Bölme İşleminin Adım Adım Gösterimi
Şimdi, 255’i 15’e bölme işlemini adım adım gösterelim.
İşlem: 255 ÷ 15
Adımlar:
-
İlk Basamak (25 ÷ 15)
- 25’in içinde 15 kaç kez var?
- 15 x 1 = 15
- Kalan: 25 - 15 = 10
-
İkinci Basamak (105 ÷ 15)
- 5’i aşağıya indirerek 105 yaparız (önceki kalan 10 ile).
- 105’in içinde 15 kaç kez var?
- 15 x 7 = 105
- Kalan: 105 - 105 = 0
Bölme İşlemindeki Tam Sonuç:
- Tam sayı kısmı: 17
- Kalan: 0
Sonuç olarak, 255’i 15’e böldüğümüzde elde edilen sonuç 17 olur. Bu işlem de elle bölme yöntemi ile yukarıda verilen adımlarda gösterildiği gibi yapılır.
Bölme İşlemlerinin Adım Adım Gösterimi
İlk İşlem: 629 ÷ 17
-
İlk Basamak (62 ÷ 17)
- 62’nin içinde 17 kaç kez var?
- 17 x 3 = 51
- Kalan: 62 - 51 = 11
-
İkinci Basamak (119 ÷ 17)
- 9’u aşağıya indirerek 119 yaparız (önceki kalan 11 ile).
- 119’un içinde 17 kaç kez var?
- 17 x 7 = 119
- Kalan: 119 - 119 = 0
Bölme İşlemindeki Tam Sonuç:
- Tam sayı kısmı: 37
- Kalan: 0
İkinci İşlem: 720 ÷ 48
-
İlk Basamak (72 ÷ 48)
- 72’nin içinde 48 kaç kez var?
- 48 x 1 = 48
- Kalan: 72 - 48 = 24
-
İkinci Basamak (240 ÷ 48)
- 0’ı aşağıya indirerek 240 yaparız (önceki kalan 24 ile).
- 240’ın içinde 48 kaç kez var?
- 48 x 5 = 240
- Kalan: 240 - 240 = 0
Bölme İşlemindeki Tam Sonuç:
- Tam sayı kısmı: 15
- Kalan: 0
Her iki işlemi de adım adım gösterdiğimizde sonuçların doğru olarak hesaplandığını görmekteyiz.