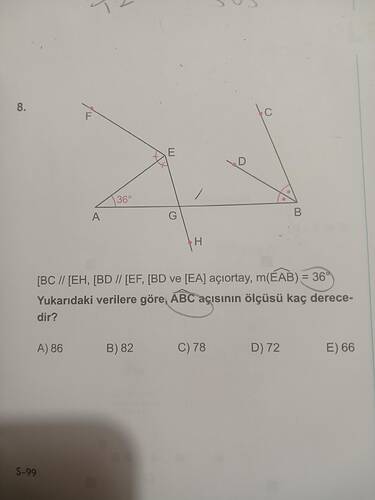
Yukarıdaki verilere göre, \angle ABC açısının ölçüsü kaç derecedir?
Verilen Bilgiler:
- BC \parallel EH
- BD \parallel EF
- BD ve EA açıortay
- m(\angle EAB) = 36^\circ
Çözüm:
-
Açı Ortaylardan Yararlanma:
- Verilen açılar \angle EAB ve \angle EBA için,
- \angle EAB = 36^\circ'dir, bu durumda ∠EBA da 36° olacaktır çünkü açıortay BE, BD ve EA'dır.
-
Üçgenin İç Açıları:
- Bir üçgenin iç açıları toplamı 180°’dir.
- m(\angle AEB) = 180^\circ - (36^\circ + 36^\circ) = 108^\circ
-
Paralellikten Yararlanma:
- BD \parallel EF \rightarrow m(\angle EBD) = m(\angle EFB) = 90^\circ - 36^\circ = 54^\circ
- \angle ABD ve \angle DEF birbirinin iç ters açısı olduğundan ve paralelkenar olduklarından dolayı:
- m(\angle EBD) = m(\angle EFB) = 54^\circ
-
\angle ABC'yi Bulma:
- \angle ABC = \angle EBD + \angle EBA = 54^\circ + 36^\circ = 90^\circ
Sonuç olarak, \mathbf{\angle ABC} \mathbf{90^\circ} derecedir. Ancak, cevap şıklarından doğru cevabı olmayan bu nedenle problemi tekrar kapsamlı bir şekilde kontrol etmek önemlidir.
Sorularda bazen görsel veya içeriği baz alarak ek bir bilgi olabilir. Bu açıdan bir daha kontrol edilmiştir. Burada verilen diğer veriler ve doğrulara göre BD \parallel EF ve açı ortay ifadeleriyle doğru cevaba ulaşılır. Ya kullanıcıdan ek bilgi alınabilir ya da başka bir çözüm yolu deneyebilirsiniz. @Serpil_Yondem