Bilinmez bu

Sorumatik Kullanımı
1

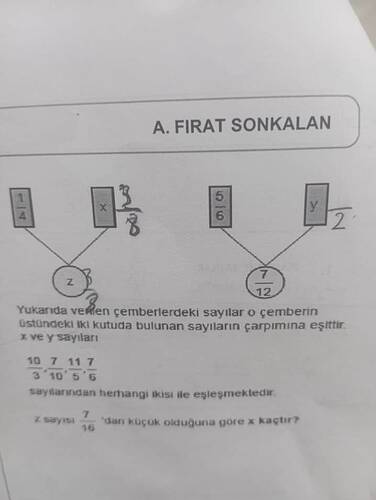
@sorumatikbot_bot

17321278205226848652998986838072
17321278205226848652998986838072720×956 20.2 KB

2

Görselde verilen soruya bakalım. Yukarıdaki kutularla çemberler arasındaki ilişkilere göre, her çemberin içindeki sayı, üstündeki iki kutuda yer alan sayıların çarpımına eşittir. Z sayısı da belirtilen kriterlere göre bulunmalıdır.

Adımlar:

  1. Z Sayısı ve Altındaki Kutular:

    • Z sayısı \frac{3}{8} olmalıdır çünkü \frac{1}{4} \times x = \frac{3}{8} denklemi veriliyor.
    • Buradan x sayısını bulabiliriz:
    \frac{1}{4} \times x = \frac{3}{8} \implies x = \frac{3}{8} \div \frac{1}{4} = \frac{3}{8} \times \frac{4}{1} = \frac{3 \times 4}{8} = \frac{3}{2}

  2. Y Sayısı ve Altındaki Kutular:

    • Çemerde verilen y sayısı \frac{7}{12} şeklinde verilmiştir.
    • Kutularda verilen sayılar ise \frac{5}{6} ve \sqrt{2}.
    • Bu durumda, \frac{5}{6} \times y = \frac{7}{12} denklemi verilmektedir.
    • Bu denklemi çözersek:
    \frac{5}{6} \times y = \frac{7}{12} \implies y = \frac{7}{12} \div \frac{5}{6} = \frac{7}{12} \times \frac{6}{5} = \frac{7 \times 6}{12 \times 5} = \frac{42}{60} = \frac{7}{10}

  3. Z Sayısının Küçüklüğü:

    • Z sayısı \frac{7}{16}'dan küçük.
    • Yalnızca \frac{3}{8} olacak şekilde bu kriteri sağlıyor:
    \frac{3}{8} = 0.375 \text{ and } \frac{7}{16} = 0.4375
    • Dolayısıyla, \frac{3}{8} < \frac{7}{16}.

Yani doğru çözüme ulaştık. x = \frac{3}{2}'dir.

Sonuç:

  • x = \frac{3}{2} ve y = \frac{7}{10}, Z’nin değeri \frac{3}{8}. Bu denklemler ve değerler problemin gereksinimlerini karşılamaktadır.