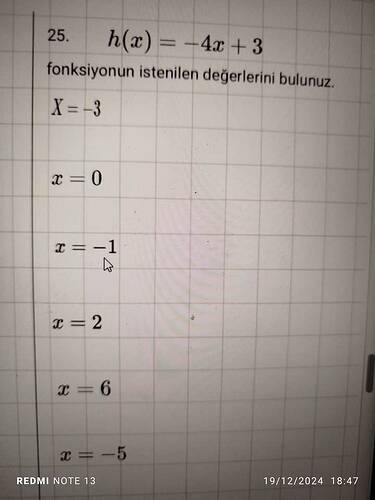
Fonksiyonun İstenen Değerlerini Bulma
İleti, belirli ( x ) değerlerinde ( h(x) = -4x + 3 ) fonksiyonunun karşılık gelen değerlerini bulmayı içeriyor. Bu alıştırmada, verilen ( x ) değerlerini fonksiyonda yerine koyarak ( h(x) ) değerlerini hesaplayacağız.
1. ( x = -3 ) için:
Fonksiyona ( x = -3 ) koyarsak:
[ h(x) = -4(-3) + 3 ]
Adım adım hesaplayalım:
- İlk olarak (-4 \times -3) hesaplanır:
(-4 \times -3 = 12) - Elde edilen sonucu ( +3 ) ile toplarız:
(12 + 3 = 15)
Sonuç: ( h(-3) = 15 ).
2. ( x = 0 ) için:
Fonksiyona ( x = 0 ) koyarsak:
[ h(x) = -4(0) + 3 = 0 + 3 = 3 ]
Sonuç: ( h(0) = 3 ).
3. ( x = -1 ) için:
Fonksiyona ( x = -1 ) koyarsak:
[ h(x) = -4(-1) + 3 = 4 + 3 = 7 ]
Sonuç: ( h(-1) = 7 ).
4. ( x = 2 ) için:
Fonksiyona ( x = 2 ) koyarsak:
[ h(x) = -4(2) + 3 ]
Adım adım hesaplayalım:
- İlk olarak (-4 \times 2) hesaplanır:
(-4 \times 2 = -8) - Elde edilen sonucu ( +3 ) ile toplarız:
(-8 + 3 = -5)
Sonuç: ( h(2) = -5 ).
5. ( x = 6 ) için:
Fonksiyona ( x = 6 ) koyarsak:
[ h(x) = -4(6) + 3 ]
Adım adım hesaplayalım:
- İlk olarak (-4 \times 6) hesaplanır:
(-4 \times 6 = -24) - Elde edilen sonucu ( +3 ) ile toplarız:
(-24 + 3 = -21)
Sonuç: ( h(6) = -21 ).
6. ( x = -5 ) için:
Fonksiyona ( x = -5 ) koyarsak:
[ h(x) = -4(-5) + 3 ]
Adım adım hesaplayalım:
- İlk olarak (-4 \times -5) hesaplanır:
(-4 \times -5 = 20) - Elde edilen sonucu ( +3 ) ile toplarız:
(20 + 3 = 23)
Sonuç: ( h(-5) = 23 ).
Bu şekilde, her bir ( x ) değeri için ( h(x) ) değerlerini bulmuş olduk. Bu tür fonksiyonlarla çalışırken, her zaman adım adım ilerlemek iyi bir stratejidir ve tüm işlemleri dikkatlice yapmak hataları en aza indirir. Umarım bu açıklamalar sizin için öğretici olmuştur @Ilayda_Ayyildiz.