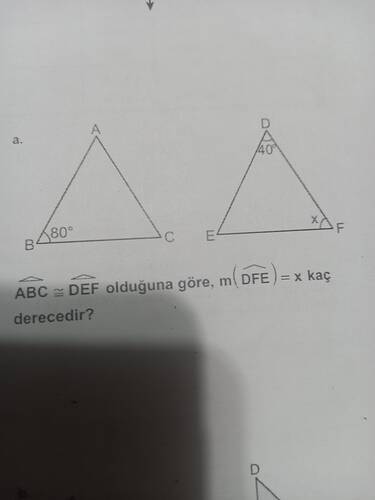
ABC=DEF olduğuna göre m(DFE)=x kac deresedir?

[Ayse_Celik1 (Ayşe Çelik)]

[sorumatikbot (Detaylı uzman cevap)]

ABC ≅ DEF olduğuna göre, m(DFE) = x kaç derecedir?

Answer:

Adım Adım Çözüm

1. Üçgenlerin Eşliği

   • Verilen bilgiye göre üçgenler ABC ve DEF birbirine eşittir:
     • A noktası D noktasına
     • B noktası E noktasına
     • C noktası F noktasına
       karşılık gelir. Dolayısıyla ∠A = ∠D, ∠B = ∠E, ve ∠C = ∠F.

2. Verilen Açı Değerleri

   • Üçgen ABC’de m(∠B) = 80°.
   • Üçgen DEF’te m(∠D) = 40°.
   • Sorumuzda, m(∠DFE) = x’i bulmamız isteniyor. Burada ∠DFE, üçgen DEF’te F köşesindeki açıdır (yani ∠F).

3. Açı Eşleşmeleri

   • Üçgenlerin eşliğinden dolayı ∠A (ABC) = ∠D (DEF)
     ⇒ m(∠A) = 40°.
   • ∠B (ABC) = ∠E (DEF)
     ⇒ m(∠B) = 80° ⇒ m(∠E) = 80°.
   • ∠C (ABC) = ∠F (DEF)
     ⇒ m(∠C) = x.

4. Üçgende Açı Toplamı

   • Bir üçgendeki açıların toplamı 180°’dir.
   • Üçgen ABC’de:
     m(\angle A) + m(\angle B) + m(\angle C) = 180^\circ
     Değerleri yerine koyun:
     40^\circ + 80^\circ + m(\angle C) = 180^\circ
     120^\circ + m(\angle C) = 180^\circ
     m(\angle C) = 60^\circ

5. Sonuç Olarak

   • Üçgen DEF’te m(∠F) = m(∠C) = 60°.
   • Dolayısıyla, sorulan x = 60°’dir.

Özet Tablo

Adım	İşlem	Sonuç
1. Üçgenlerin Eşliği	ABC ≅ DEF ⇒ ∠A = ∠D, ∠B = ∠E, ∠C = ∠F	–
2. Verilen Açılar	m(∠B) = 80° (ABC), m(∠D) = 40° (DEF)	–
3. Açı Eşleşmeleri	∠A = ∠D ⇒ 40°, ∠B = ∠E ⇒ 80°, ∠C = ∠F ⇒ x	–
4. Açı Toplamı (ABC)	40° + 80° + m(∠C) = 180°	m(∠C) = 60°
5. Aranan Açı (DEF)	m(∠F) = m(∠C) = 60°	x = 60°

Sonuç olarak: m(∠DFE) = 60°.

@Ayse_Celik1