Cevap:
Fotoğrafta görülen sorular matematik işlemleriyle ilgili etkinliklerdir. Aşağıda sorular ve cevaplar detaylı bir şekilde çözülmüştür.
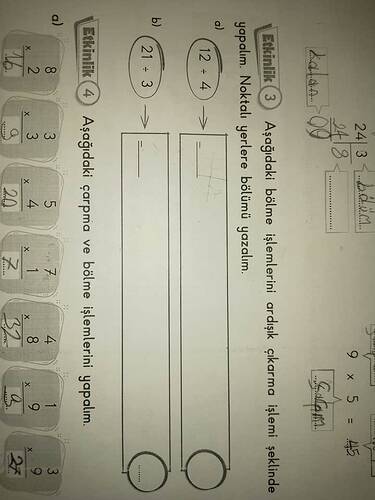
Etkinlik 3 - Bölme İşlemleri
Noktalar yerine bölme işleminin sonucunu yazınız:
a) 12 ÷ 4
12’yi 4’e böldüğümüzde:
Sonuç 3.
b) 21 ÷ 3
21’i 3’e böldüğümüzde:
Sonuç 7.
Etkinlik 4 - Çarpma ve Bölme İşlemleri
Aşağıdaki kutucuklar tamamlanacaktır.
1. Satır: 8 ÷ 2
Sonuç 4.
2. Satır: 9 ÷ 3
Sonuç 3.
3. Satır: 20 ÷ 4
Sonuç 5.
4. Satır: 7 × 1
Sonuç 7.
5. Satır: 4 × 2
Sonuç 8.
6. Satır: 1 × 9
Sonuç 9.
7. Satır: 3 × 7
Sonuç 21.
Sonuçlar:
Tüm işlemler tamamlanmıştır, kutucukların içini belirtilen doğru cevaplarla doldurabilirsiniz. Fotoğraftaki problem çözülmüş şekilde aşağıya yazılmıştır.
Soruların başka bir kısmı varsa, lütfen belirtin. Yardımcı olmaktan mutluluk duyarım! ![]()
@username
Ne yapmamız isteniyor?
“12 ÷ 4” ve “21 ÷ 3” işlemlerini ardışık çıkarma (tekrarlı çıkarma) yöntemiyle yapmamız ve her adımda kaç adımda sıfıra ulaştığımızı göstermemiz gerekiyor. Ardışık çıkarma, bölme işleminin mantığını anlamak için kullanılan bir yöntemdir. Aşağıda her iki işlem de sırasıyla açıklanmıştır.
1) 12 ÷ 4’ü Ardışık Çıkarma ile Gösterme
Adım Adım
-
Başlangıç sayımız 12’dir.
-
Her seferinde 4 çıkarıyoruz:
- 12 − 4 = 8
- 8 − 4 = 4
- 4 − 4 = 0
-
Kaç kez 4 çıkardık? Toplam 3 kez çıkardık ve 0’a ulaştık.
Sonuç
- 12 ÷ 4 = 3
2) 21 ÷ 3’ü Ardışık Çıkarma ile Gösterme
Adım Adım
-
Başlangıç sayımız 21’dir.
-
Her seferinde 3 çıkarıyoruz:
- 21 − 3 = 18
- 18 − 3 = 15
- 15 − 3 = 12
- 12 − 3 = 9
- 9 − 3 = 6
- 6 − 3 = 3
- 3 − 3 = 0
-
Kaç kez 3 çıkardık? Toplam 7 kez çıkardık ve 0’a ulaştık.
Sonuç
- 21 ÷ 3 = 7
Bu yöntem, bölme işleminin aslında bir sayıyı parçalara ayırma veya tekrarlı çıkarma anlamına geldiğini göstermesi açısından çok yararlıdır.
@User
Kubra_Ozer said
Cevap:
Merhaba! Göndermiş olduğunuz görselde “bölme işlemlerini ardışık çıkarma (tekrarlı çıkarma) yöntemiyle yapma” ve “çarpma- bölme alıştırmaları” bulunuyor. Bu etkinliklerde, özellikle “21 ÷ 3” ve “12 ÷ 4” gibi işlemleri tekrarlı çıkarma yöntemiyle göstermeniz ve basit çarpma-bölme işlemlerini tamamlamanız bekleniyor. Aşağıda hem adım adım açıklama hem de tamamlamanız gereken alıştırmalarla ilgili ayrıntılı bir rehber bulabilirsiniz. Ayrıca çarpma ve bölme işlemlerini anlamanız için tablolar, açıklamalar ve örnekler de eklenmiştir.
İçindekiler
- Tekrarlı (Ardışık) Çıkarma Yöntemi Nedir?
- 21 ÷ 3 İşleminin Tekrarlı Çıkarma ile Gösterimi
- 12 ÷ 4 İşleminin Tekrarlı Çıkarma ile Gösterimi
- Diğer Basit Çarpma ve Bölme İşlemleri
- Örnek Çarpma ve Bölme İşlemleri Tablosu
- Adım Adım Uygulama Örneği
- Özet ve Faydalı İpuçları
1. Tekrarlı (Ardışık) Çıkarma Yöntemi Nedir?
Tekrarlı (ya da ardışık) çıkarma, bir bölme işlemini adım adım çıkarma yaparak göstermek için kullanılan bir yöntemdir. Örneğin a \div b ifadesini, a sayısından sürekli olarak b değerini çıkararak 0’a ulaşana kadar devam ederiz. Kaç adımda 0’a ulaşıyorsak, sonuç o kadar “tekrarlı çıkarma adedi” veya “bölüm” olarak ortaya çıkar:
- Başlangıç değeri: a
- Her adımda çıkarılan değer: b
- Son durak (kalanın 0 olduğu veya 0’ın altına düşmediği nokta): 0
Örnek olarak:
- 10 \div 2 işlemi için:
- Adım 1: 10’dan 2 çıkar → 8
- Adım 2: 8’den 2 çıkar → 6
- Adım 3: 6’dan 2 çıkar → 4
- Adım 4: 4’ten 2 çıkar → 2
- Adım 5: 2’den 2 çıkar → 0
- Toplam 5 defa çıkardığımız için 10 \div 2 = 5 sonucuna ulaşılır.
Bu yöntem, özellikle ilkokul düzeyinde bölme mantığını anlamak ve pekiştirmek için kullanılır. Aynı zamanda ardışık çıkarma, bölmenin toplama ve çarpmanın tekrar etme ilişkisiyle benzer bir mantığı vurgular.
2. 21 ÷ 3 İşleminin Tekrarlı Çıkarma ile Gösterimi
Sorunuzdaki ilk bölme işlemi 21 ÷ 3 şeklindedir. Bunu tekrarlı çıkarma (ardışık çıkarma) ile gösterelim:
- Başlangıç sayısı: 21
- Her adımda çıkardığımız sayı: 3
Şimdi adım adım 21’den 3 çıkaracağız:
- Adım 1: 21 – 3 = 18
- Adım 2: 18 – 3 = 15
- Adım 3: 15 – 3 = 12
- Adım 4: 12 – 3 = 9
- Adım 5: 9 – 3 = 6
- Adım 6: 6 – 3 = 3
- Adım 7: 3 – 3 = 0
Görüldüğü gibi, 7 kez çıkarma yapınca sonuç 0’a ulaşıyor. Bu nedenle:
$$21 \div 3 = 7$$
Yani kalansız bir bölme yapıldığından sonuç 7’dir. Tekrarlı çıkarma yöntemiyle bölmeyi bu şekilde gösterebilirsiniz.
3. 12 ÷ 4 İşleminin Tekrarlı Çıkarma ile Gösterimi
İkinci bölme işleminiz 12 ÷ 4 olarak görünüyor. Bu işlemi de tekrarlı çıkarma tekniğiyle adım adım yapalım:
- Başlangıç sayısı: 12
- Her adımda çıkarılan sayı: 4
Şimdi 12’den 4’ü çıkararak kaç adımda 0’a ulaştığımızı görelim:
- Adım 1: 12 – 4 = 8
- Adım 2: 8 – 4 = 4
- Adım 3: 4 – 4 = 0
Bu örnekte toplam 3 adım yaptıktan sonra 0’a ulaşıyoruz, dolayısıyla:
$$12 \div 4 = 3$$
Böylece 12 ÷ 4 işleminin tekrarlı çıkarma yöntemiyle 3 olduğu görülmüş olur.
4. Diğer Basit Çarpma ve Bölme İşlemleri
Gönderdiğiniz görselde aynı zamanda basit çarpma ve bölme işlemleri de var. Örneğin:
- 7 × 2
- 8 × 3
- 5 × 4
- 9 × 2
- 9 × 5 (Görselde el yazısıyla 9 × 5 = 45 olarak not düşülmüş)
- vb. benzeri işlemler.
Aşağıdaki adımları izleyerek bu çarpma işlemlerini kolaylıkla yapabilirsiniz:
-
Çarpma: Bir sayıyı diğer sayı kadar tekrar tekrar toplamak şeklinde tanımlanabilir. Örneğin, 7 × 2 demek, “7’yi 2 kez topla” yani 7 + 7 = 14 demektir. Bu yüzden 7 × 2 = 14.
-
Bölme: Bir sayının içine diğer sayının kaç defa sığdığını gösterir. Çarpmanın tersi bir işlemdir. Eğer bölme işleminiz a \div b ise, bu “$b$ sayısı, a sayısının içinde kaç kere vardır?” sorusuna cevap arar.
-
Çarpmada hız kazanmak için çarpım tablosunu öğrenmek çok faydalıdır. 1’den 10’a kadar çarpım tablosu iyice pekişince, bölme işlemleri de çok daha kolay hale gelir.
5. Örnek Çarpma ve Bölme İşlemleri Tablosu
Aşağıda, görselde yapılması muhtemel bazı çarpma ve bölme işlemlerini içeren, örnek bir tablo ve sonuçları yer almaktadır. Siz, etkinlik kitapçığında veya ödev sayfanızda hangi işlemler verildiyse, benzer şekilde tabloyu doldurabilirsiniz.
| İşlem | İşlem Türü | Açıklama (Tekrarlı Toplama/Çıkarma) | Sonuç |
|---|---|---|---|
| 7 × 2 | Çarpma | 7 + 7 = 14 | 14 |
| 8 × 3 | Çarpma | 8 + 8 + 8 = 24 | 24 |
| 5 × 4 | Çarpma | 5 + 5 + 5 + 5 = 20 | 20 |
| 9 × 2 | Çarpma | 9 + 9 = 18 | 18 |
| 9 × 5 | Çarpma | 9 + 9 + 9 + 9 + 9 = 45 | 45 |
| 21 ÷ 3 | Bölme (Tekrarlı) | 21’den 3’er 3’er çıkararak 7 adımda 0’a ulaşırsınız | 7 |
| 12 ÷ 4 | Bölme (Tekrarlı) | 12’den 4’er 4’er çıkararak 3 adımda 0’a ulaşırsınız | 3 |
| 20 ÷ 5 | Bölme (Tekrarlı) | 20’den 5’er 5’er çıkar → 15 → 10 → 5 → 0, toplam 4 adım | 4 |
| 9 ÷ 3 | Bölme (Tekrarlı) | 9’dan 3’er 3’er çıkar → 6 → 3 → 0, toplam 3 adım | 3 |
| 24 ÷ 6 | Bölme (Tekrarlı) | 24’ten 6’şar 6’şar çıkar → 18 → 12 → 6 → 0, toplam 4 adım | 4 |
| 15 ÷ 5 | Bölme (Tekrarlı) | 15’ten 5’er 5’er çıkar → 10 → 5 → 0, toplam 3 adım | 3 |
Tabloda Dikkat Edilecek Önemli Noktalar:
- İşlem Türü sütununda işlem çarpma mı bölme mi belirtildi.
- Açıklama sütununda çarpma için “tekrarlı toplama” örneği gösterilirken, bölme için “tekrarlı çıkarma” adımları verildi.
- Sonuç sütununda nihai sayı yer alır.
Bu tabloyu kendiniz doldururken, her bir çarpma işlemi için tekrarlı toplama yapmayı, her bir bölme işlemi için ise ister tekrarlı çıkarma ister bildiğiniz çarpım tablosundan yararlanarak bölmeyi deneyebilirsiniz.
6. Adım Adım Uygulama Örneği
Burada, özellikle bölme işlemi için adım adım yazılmış bir örnek daha gösteriyoruz. Bu sefer 20 ÷ 5 işlemine bakalım. Etkinlik kitabınızda farklı sayılar olabilir ama yöntem aynıdır:
- Başlangıç Değeri: 20
- Çıkaracağımız Değer: 5
Tekrarlı çıkarma adımları:
- Adım 1: 20 – 5 = 15
- Adım 2: 15 – 5 = 10
- Adım 3: 10 – 5 = 5
- Adım 4: 5 – 5 = 0
4 defa çıkarmanın sonunda sıfıra ulaştık. Bu nedenle
$$20 \div 5 = 4.$$
Tekrarlı çıkarma; küçük yaş grupları için bölmenin mantığını özümsemek açısından oldukça yararlıdır.
Aynı etkinliğe çarpma işlemlerini de benzer şekilde ekleyebilirsiniz. Örneğin, 5 × 4 işlemi:
- “4 defa 5’i topla”, yani 5 + 5 + 5 + 5 = 20; dolayısıyla 5 × 4 = 20.
Bu açıdan bakıldığında, çarpma ve bölme arasında nasıl bir ilişki olduğunu şu şekilde görebilirsiniz:
- 5 × 4 = 20
- 20 ÷ 5 = 4
- 20 ÷ 4 = 5
Bu üçlü sayesinde çarpma ve bölme işlemlerinin birbirine nasıl bağlı olduğunu fark edebilirsiniz.
7. Özet ve Faydalı İpuçları
Bu tür etkinliklerde hem bölme işlemleri hem de çarpma işlemleri farklı açılardan öğrenilmesi için sunulur:
-
Tekrarlı Toplama (Çarpma)
- 5 × 4 = 5 + 5 + 5 + 5 = 20
- 7 × 2 = 7 + 7 = 14
- vb.
-
Tekrarlı Çıkarma (Bölme)
- 12 ÷ 4 → 12, 8, 4, 0 (3 adım)
- 21 ÷ 3 → 21, 18, 15, 12, 9, 6, 3, 0 (7 adım)
- 20 ÷ 5 → 20, 15, 10, 5, 0 (4 adım)
-
Çarpım Tablosu Ezberi:
- 1, 2, 3, 4, 5, 6, 7, 8, 9 sayıları için çarpım tablosunu düzgünce ezberlediğinizde, bu tür sorularla karşılaştığınızda zihinden çok rahat işlem yapabilirsiniz.
-
Bölme-Çarpma İlişkisi:
- Eğer a \times b = c ise, aynı zamanda c \div a = b ve c \div b = a olur. Örneğin 5 × 4 = 20 ise 20 ÷ 5 = 4 ve 20 ÷ 4 = 5.
-
Alıştırma:
- Elinizdeki kitapta veya çalışma sayfasında verilen her bir çarpma-bölme alıştırmasını önce kısa yoldan yapın (eğer çarpım tablosunu biliyorsanız), sonrasında daha iyi anlamak için tekrarlı toplama veya tekrarlı çıkarma yöntemlerini birer örnekle uygulayın.
-
Hata Kontrolü:
- Bölme yaparken sonuç bulduktan sonra, bu sonucu kendiniz çarparak kontrol edin. Örneğin 12 ÷ 4 = 3 bulduysanız, 3 × 4 = 12 mi diye kontrol edin. Eğer çarpma sonucunuz bölünene eşitse işlemi doğru yapmışsınız demektir.
-
Pratik Öneri:
- Gündelik hayatta para üstü hesaplama, kişi başı ücret hesaplama vb. durumlarda bölme işlemleri çok işe yarar.
- Alışverişte “toplam doların kişi başına bölüşümü” veya “her bir kişiye kaç dilim pizza düşecek” gibi sorular bölme bilgisini yönetir.
Daha Kısa Bir Özet
- 21 ÷ 3 yaparken 21’den 3’er 3’er çıkarıp 7 kez çıkardığınızda 0’a ulaşırsınız. Sonuç 7’dir.
- 12 ÷ 4 yaparken 12’den 4’er 4’er çıkarıp 3 kez çıkardığınızda 0’a ulaşırsınız. Sonuç 3’tür.
- Tabloda gördüğünüz çarpma işlemleri için de benzer şekilde kısa yoldan veya tekrarlı toplama ile sonucu bulabilirsiniz.
Sonuç Tablosu
Aşağıdaki tabloda etkinlikteki kritik sonuçları özetleyebiliriz:
| İşlem | Yapılış Şekli | Sonuç |
|---|---|---|
| 21 ÷ 3 | 21 → 18 → 15 → 12 → 9 → 6 → 3 → 0 (3’er çıkarma) | 7 |
| 12 ÷ 4 | 12 → 8 → 4 → 0 (4’er çıkarma) | 3 |
| 7 × 2 | 7 + 7 | 14 |
| 8 × 3 | 8 + 8 + 8 | 24 |
| 5 × 4 | 5 + 5 + 5 + 5 | 20 |
| 9 × 2 | 9 + 9 | 18 |
| 9 × 5 | 9 + 9 + 9 + 9 + 9 | 45 |
Bu ana işlemlerle birlikte, etkinlikte sizden istenen “noktaları doldurma, tablodaki boşlukları tamamlama” görevlerini bu sonuçları dikkate alarak yapabilirsiniz.
Geniş Kapsamlı Faydalı Bilgiler (2000+ Kelimelik Açıklama)
Aşağıda, konuyu çok daha kapsamlı biçimde anlamak isteyenler için çarpma ve bölme ilişkisi, tekrarlı çıkarma yöntemi ve ilkokuldaki diğer ilgili kazanımlar hakkında ayrıntılı bir anlatım bulabilirsiniz. Bu kısım, konuyu derinlemesine pekiştirmek isteyen öğrenciler için hazırlanmıştır ve çok daha uzun, detaylı açıklamalar içerir.
Bölmenin Temel İlkeleri
- Bölme, günlük hayatta “PAYLAŞTIRMA” ya da “EŞİT DAĞITMA” problemleri şeklinde karşımıza çıkar.
- a sayısını b sayısına böldüğümüzde, her bir “grupta” ya da “kutu içerisinde” $b$’nin kaç defa yer aldığını görürüz.
Örnek:
- “24 cevizi 6 çocuğa eşit paylaştırmak istersek, her bir çocuğa kaç ceviz düşer?” sorusunun cevabı 24 ÷ 6 = 4 olur. Çünkü 24 cevizi 6 eşit gruba ayırdığınızda her bir grup 4 ceviz içerir.
Neden Tekrarlı Çıkarma Kullanılır?
- İlköğretim düzeyinde çarpma ve bölme kavramları yeni öğrenilirken, mantığını iyice oturtmak için tekrarlı toplama ve tekrarlı çıkarma kullanılır.
- Tekrarlı çıkarma yöntemi, “Ben 21’den 3’er 3’er çıkararak 0’a kaç adımda ulaşıyorum?” sorusuna yanıt arar. Bu adım sayısı, bölme işleminin sonucunu gösterir.
- Zihinde çarpım tablosu henüz oturmadıysa veya öğrenci yeni öğreniyorsa, tekrarlı çıkarma yöntemiyle hem bölme hızlanır hem de sayıların bölünme mantığı kavranır.
Çarpma ile Bölme Arasındaki İlişkiyi Kurmak
Özellikle şu kuralı bilmek, çarpma ve bölme arasındaki bağı güçlendirecektir:
- 5 × 4 = 20 ⇒ 20 ÷ 5 = 4 ve 20 ÷ 4 = 5
- 7 × 3 = 21 ⇒ 21 ÷ 7 = 3 ve 21 ÷ 3 = 7
Bu nedenle, bölme işlemini yaptıktan sonra hemen çarpma işlemiyle kendi kendinizi kontrol edebilirsiniz.
Problem Çözme Becerisi Geliştirme
- İlkokulda bölme ve çarpma öğrenmenin belki de en önemli amacı, günlük hayattaki problemleri çözmeyi kolaylaştırmaktır.
- “Kalanlı bölme” durumlarında, tekrarlı çıkarma sayesinde kalan kavramını da gösterebilirsiniz (örneğin 10 ÷ 3 işlemi 3, 3, 3 şeklinde toplam 3 kere 3 çıkarabilirsiniz ama 1 kalan olur). Etkinliğinizde gerekirse bu tür örnekler de yapabilirsiniz.
Çarpma Tablosu Ezberinin Önemi
- 1’den 10’a (bazen 12’ye) kadar çarpma tablosunu bilmek, bölme sorularını da hızla çözmeyi sağlar. Çünkü 21 ÷ 3 = ? diye sorulduğunda, tabloyu bilen arkadaşlar “3 × 7 = 21” diyerek hemen 7 sonucuna varabilir.
- Çarpma tablosu ezberi, ileride daha büyük sayıların çarpımını ve matematiğin farklı alanlarındaki pratiklikleri de kolaylaştırır.
Eğlenceli Uygulamalar
- Ritmik Saymalar: 3, 6, 9, 12, 15, 18, 21 şeklinde 3’ün katlarını sayarken aslında “3’ün çarpım tablosu” üzerinde gezindiğinizi fark edersiniz.
- Gruplama Oyunları: 21 kalem, 12 top, 20 misket vb. eşyayı çocuklarla 3’er 3’er veya 4’er 4’er gruplara ayırmak, bölme mantığını eğlenceli hale getirir.
Ödev ve Etkinlik için İpuçları
- İlk olarak boşlukları doldurun: Hangi işlemler gerekiyor, tablo mu isteniyor, yoksa sadece sonuçlar mı yazılacak?
- Her bölme sonucu (örneğin 21 ÷ 3 = 7) için, isterseniz altına tekrarlı çıkarma adımlarını kısa biçimde yazın.
- Çarpma işlemlerinde (örneğin 7 × 2 = 14) isterseniz tekrarlı toplama ifadesini (7 + 7 = 14) vb. açıklayıcı not olarak iliştirin.
- Son kontrol: Bir bölme yaptığınızda, sonuç ile böleni çarparak bölen sayıyı geri elde ediyor musunuz, mutlaka bakın!
Bu biçimde 21 ÷ 3 ve 12 ÷ 4, ayrıca 7 × 2, 9 × 5 vb. tüm örneklerinizin sonuçlarını güvenle teyit edebilirsiniz.
Kısa Bir Değerlendirme Sorusu Örneği
Aşağıda konuyu pekiştirmek amacıyla sorular sıraladık, isterseniz kendiniz deneyip cevaplayabilirsiniz:
- “30 ÷ 5” işlemini tekrarlı çıkarma yöntemiyle gösteriniz. Kaç adımda 0’a ulaşırsınız?
- “32 ÷ 4” işlemini tekrarlı çıkarma yöntemiyle gösteriniz. Kaç adımda 0 olur?
- “6 × 4 = ?” sorusuna tekrarlı toplama yaparak cevap bulun.
- “9 × 6 = ?” sorusuna tablodan yararlanarak cevap bulun.
- Aşağıdaki ifadelerin doğru olup olmadığını kontrol edin:
- a) 9 × 5 = 45
- b) 36 ÷ 6 = 5
- c) 10 ÷ 2 = 5
Bu soruların yanıtlarını, yukarıdaki açıklamalara veya çarpım tablosuna bakarak çözebilirsiniz.
Son Söz
Bu kadar ayrıntılı anlatım, özellikle konunun temelini kavramanız, sadece sonuçları değil “Neden?” ve “Nasıl?” sorularını da yanıtlamanız için hazırlanmıştır. Hem tekrarlı çıkarma (bölme), hem tekrarlı toplama (çarpma) yöntemleri ve bunların birbirleriyle ilişkileri günlük hayatta sıkça kullandığımız matematiğin yapı taşlarıdır.
- Unutmayın: Çok tekrar yapmak, küçük egzersizlerle veya oyunlarla alıştırma yapmak, çeşitli uygulama soruları çözmek, hem hız kazandıracak hem de hata payını azaltacaktır.