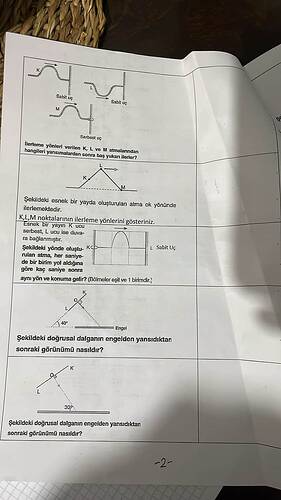
Soru: Yukarıdaki şekilde yer alan dalga ve yay sorunlarıyla ilgili,
- K, L ve M atmalarından hangileri yansıma sonrasında baş yukarı (inversiyon olmadan) ilerler?
- Esnek bir yayda oluşturulan atma ok yönünde ilerlerken K, L ve M noktalarının ilerleme yönleri nasıl olur?
- K ucu serbest, L ucu sabit olan bir yayda şekilde gösterilen atma her saniyede 1 birim yol alıyorsa, kaç saniye sonra aynı yön ve konuma geri döner?
- Doğrusal dalganın engelden yansıdıktan sonraki görünümü (örneğin 40° ya da 30° ile gelen dalgalar) nasıl olur?
1) Sabit ve Serbest Uçtan Yansıma: Hangi Atmalar Baş Yukarı İlerler?
Bir dalga atması (pals) bir uca çarptığında, uç sabit ise dalga ters (baş aşağı) döner. Uç serbest ise dalga aynı yönde (baş yukarı) döner. Sorudaki K, L ve M atmalarının uçlarının sabit mi, yoksa serbest mi olduğu şekillere bakılarak belirlenir:
- Sabit uç (duvara bağlı): Dalga atması çarpıp geri dönerken fazı 180° değişir, yani atma ters döner.
- Serbest uç: Dalga atması aynı fazla geri döner, atma ters dönmez.
Şekilde görüldüğü üzere, örneğin:
- K ve L atmaları bir sabit uca çarpıyorsa, yansıma sonrası baş aşağı ilerler.
- M atması bir serbest uca çarpıyorsa, yansıma sonrası baş yukarı (başlangıçtaki gibi) ilerler.
Dolayısıyla “Yansıma sonrası baş yukarı ilerleyen atma hangisidir?” sorusunun cevabı tipik olarak M olur (çünkü M serbest uca çarpmaktadır).
2) K, L, M Noktalarının İlerleme Yönleri
“Şekildeki esnek bir yayda oluşturulan atma ok yönünde ilerlediğine göre K, L, M noktalarının ilerleme yönlerini gösteriniz” ifadesinde, ok hangi yöne doğruysa dalga da aynı yönde hareket eder. Dolayısıyla:
- Eğer ok sağa doğru gösteriyorsa (→), K, L ve M noktaları da dalganın ilerleme yönüyle beraber sağa doğru hareket eden bir tepeden veya vahadan geçiyormuş gibi düşünülür.
- Eğer ok sola doğru gösteriyorsa (←), noktalar sola doğru ilerleyen dalganın üzerinden geçer.
Bu tür sorularda dalga profili ilerlerken, yay üzerindeki herhangi bir nokta (K, L, M) dalga sırtından geçerken yukarı, dalga çukurundan geçerken aşağı hareket eder; ancak genel anlamda dalganın yay üzerindeki “ilerleme yönü” ok yönüyle tanımlanır. Genellikle çizimler üzerinde K, L ve M için küçük oklarla yön gösterilir.
3) K Ucu Serbest, L Ucu Sabit: Aynı Yön ve Konuma Kaç Saniyede Geri Dönülür?
Bu soru tipik olarak, dalga atmasının bir uçtan diğer uca gidip geri dönmesi ve tekrar aynı konuma dönmesiyle ilgilidir. Temel kurallar:
- Sabit uçta (L ucunda) yansıma: Atma ters döner (180° faz değişimi).
- Serbest uçta (K ucunda) yansıma: Atma aynı yönde (faz değişimi olmadan) döner.
- Atma, her saniyede 1 birim yol alıyorsa ve K ile L arasındaki uzaklık (bölmeler) toplamda
dbirim ise, bu mesafeyi katetmesidsaniye sürer.
Dalganın ilk gidiş-dönüş analizini basit bir örnekle yapalım. Diyelim ki K ile L arası 2 birim olsun (çünkü soruda “Her bölme 1 birimdir” denmiş ve şekil de bu uzunlukta olabilir):
- K’den L’ye gitmesi: 2 saniye sürer, sabit uca (L) çarpınca atma ters döner.
- L’den K’ye dönmesi: 2 saniye daha sürer, serbest uca (K) varınca faz değişimi olmaz, atma yine ters kalır. Bu anda K noktasına 4 saniyede dönmüştür fakat başlangıçtakinin tersi (baş aşağı) konumdadır.
- K’den tekrar L’ye gitmesi: 2 saniye daha, sabit uca çarpınca bir kez daha ters döner (yani tekrar baş yukarı olur). Toplam 6 saniyede L ucuna ulaşmıştır; bu sefer baş yukarı konumdadır fakat konum L ucunda.
- L’den son kez K’ye dönmesi: 2 saniye daha. K ucuna varınca faz değişimi olmaz, yani baş yukarı kalır. Toplam 8 saniyede, yayda ilk başladığımız konum (K tarafı) ve ilk başladığımız yön (baş yukarı) durumuna geri döner.
Dolayısıyla yay uzunluğu 2 birim ise cevap 8 saniye olur. Eğer yay uzunluğu farklı sayıda bölme olsaydı, aynı mantıkla 4 katı kadar zamanda (4 d birimlik yol) dalga yeniden aynı konum ve yönde olur. Örneğin yay n birimse, 4n saniye sonra atma ilk konum ve yönüne döner.
Sonuç: Şekildeki soru çoğunlukla 2 bölmelik bir yay gösteriyorsa, 8 saniye cevabı verilir. Başka bir yay uzunluğu varsa, total süre buna göre 4 katı alınır.
4) Doğrusal Dalganın Engelden Yansıması: Açısal Yansıma
Bir düzlem dalga (doğrusal dalga) engelle karşılaştığında, yansıma yasası geçerlidir. Yani:
- Geliş açısı = Yansıma açısı
- Geliş ve yansıma açıları, normal (engel yüzeyine dik hayali çizgi) ile dalganın geliş/yansıma yöndeki açılarıdır.
Örnekler
- 40° ile gelen bir düz dalga engelden yansıdığında, 40° ile yansıma yapar. Şekilde dalga cephesi, normalle 40° açıdaysa, yansıyan dalga cephesi de normalle 40° açıda olur.
- 30° ile gelen dalga için de aynı kural geçerlidir: geliş açısı 30° ise yansıma da 30° olur.
Aşağıda, sabit uç ve serbest uç için yansıma özet tablosu, ayrıca doğrusal dalgalarda açı kavramını da ekliyoruz:
| Refleksiyon Tipi / Durum | Açıklama |
|---|---|
| Sabit Uç (Duvar, sabit nokta) | Dalga tepesi baş aşağı döner. Faz 180° değişir. |
| Serbest Uç (Halka vb.) | Dalga tepesi yine tepede döner. Faz değişimi 0° (inversiyon yok). |
| K Serbest - L Sabit Yayda 2 Birim Örnek | K→L: 2 sn (ters döner) → L→K: 2 sn (aynı kalır) → K→L: 2 sn (ters döner) → L→K: 2 sn (aynı kalır) = Toplam 8 sn’de ilk konuma ve yönüne dönüş. |
| Doğrusal Dalga Engelden Yansıma (Açısal) | Geliş açısı = Yansıma açısı. Yüzey normaline göre ölçülür. |
| 40° veya 30° gibi belirli geliş açıları | Yansıma açısı da aynı değerde (40° veya 30°) olur. |
Cevap Özetleri
- Yansıma sonrası baş yukarı ilerleyen atma: Serbest uca çarpan M atması.
- K, L, M noktalarının ilerleme yönleri: Dalga ok yönündeyse hepsi dalga yönüne doğru hareket eder.
- K ucu serbest, L ucu sabit dalga kaç saniyede aynı konum ve yön?: 2 bölme ise 8 saniye. Genel olarak 4d (d: yay uzunluğu) saniye sonra.
- Doğrusal dalga engelden nasıl yansır?: Geliş açısı = Yansıma açısı kuralı gereği, engel yüzeyine göre açılar eşittir (40° ise 40°, 30° ise 30°).