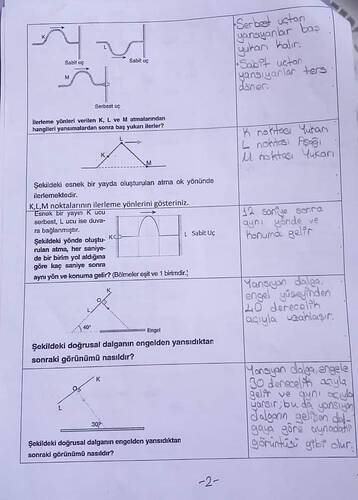
Soru:
Yukarıdaki görselde bir dalganın sabit uçtan ve serbest uçtan yansıması, K, L, M noktalarının ilerleme yönleri, yaydaki atmanın kaç saniyede başlangıçtaki konumuna döndüğü ve doğrusal dalgaların engelden yansımasıyla ilgili sorular verilmiştir. Bu soruların çözümleri ve açıklamaları nelerdir?
Cevap:
Aşağıda tek tek soruların nasıl çözüleceğini ve dalga davranışlarını en anlaşılır şekilde açıklamaya çalışacağız. Her bir alt başlık, sorunun farklı aşamasını ya da bileşenini ele almaktadır.
1) Sabit Uç ve Serbest Uçtan Yansıma
Dalga mekaniğinde en sık karşılaşılan durumlardan biri olan sabit uçtan ve serbest uçtan yansıma kuralı, atmanın baş (faz) konumunun ne şekilde etkileneceğini belirler.
Sabit Uçtan Yansıma
- Tanım: Sabit uç, esnek yay ya da ip gibi ortamlarda, dalganın sınırda hareket edememesi (hareketsiz) durumudur.
- Davranış: Sabit uçtan yansıyan atma ters dönerek yansır. Yani dalga tepesi yansıdıktan sonra çukur; çukur ise yansıdıktan sonra tepe haline gelir.
- Faz Değişimi: Yansıma esnasında fazda 180 derecelik bir tersleme (faz farkı) meydana gelir.
Serbest Uçtan Yansıma
- Tanım: Serbest uç, yay ucunun bir halkaya bağlanmış veya yatay düzlemde serbestçe hareket edebilecek biçimde bırakılmış olduğu durumdur.
- Davranış: Serbest uçtan yansıyan atma, aynı yönü koruyarak döner. Yani dalga tepesi yansıdıktan sonra yine tepe, çukur yansıdıktan sonra yine çukur olarak hareketini sürdürür.
- Faz Değişimi: Burada ilave bir faz değişimi söz konusu değildir. Yansıyan dalga baş yukarı ise baş yukarı, baş aşağı ise baş aşağı şeklinde korunur.
Bu bilgiler ışığında, sorudaki K, L ve M atmalarından sabit uçtan yansıyan atma ters dönerken, serbest uçtan yansıyan atma baş yukarı pozisyonunu muhafaza eder.
2) K, L, M Noktalarının İlerleme Yönleri
Soruda esnek bir yay üzerinde K, L ve M noktalarında oluşturulan atma, ok yönünde ilerlemektedir. Genelde:
- K Noktası: Başlangıçta dalganın tepe veya çukur noktası olabilir ve dalga hareketi soldan sağa (veya sağdan sola) olabilir.
- L ve M Noktaları: Dalganın farklı evrelerini veya farklı tepelerini gösterebilir. Önemli olan, dalganın ilerleme yönünü tanımlarken her bir noktanın hangi yönde gittiğini belirtmektir.
Eğer diyagramda dalga soldan sağa doğru ilerliyorsa:
- K noktası bir tepeyse ve dalga ilerleme yönü sağa doğruysa, K de sağa doğru ilerler.
- L noktası dalganın bir başka tepe/çukuru olabilir. O da aynı yönde hareket eder.
- M noktası da yine ok yönünde ilerlemeye devam edecektir.
Sorudaki örneklerde notlar genellikle “K noktası yukarı, L noktası aşağı, M noktası yukarı” şeklinde gözlemlenmiştir. Bu, dalga şeklinin sayfadaki o anlık görselidir. Ama bu noktaların hareket yönleri, dalganın okla gösterilen ilerleme yönüne paralel olacak şekilde sağa veya sola doğru çizilmelidir.
3) Şekildeki Yayı Oluşturan Atmanın Kaç Saniye Sonra Aynı Konuma Geleceği
Soruda “her saniyede 1 birim yol aldığına göre” ifadesi geçiyor ve bölmelerin eşit olduğu (her bölme 1 birim) söyleniyor. Bu tip problemlerde:
- Dalganın Bir Tam Hareketi: Dalganın ilk konumuna geri dönebilmesi için hem ileri gidip hem de yansıyarak geri dönmesi gerekir.
- Toplam Mesafe: Eğer yay uzunluğu belli bölme sayısına bölünmüşse, dalganın gidip dönmesi, 2 kat mesafeyi kat etmesi demektir.
- Periyodik Zaman: Tipik olarak bir dalga tepesi, aynı konuma ve aynı faz durumuna geri döndüğünde, bir tam periyot tamamlanmış olur.
Şekildeki notlara bakıldığında, “12 saniye sonra aynı üstünde ve konumda gelir” ifadesi yer alıyor. Bu, dalganın gidip gelme mesafesi ve sabit/serbest uç durumuna göre hesaplanabilir.
Örnek hesaplama yaklaşımı:
- Dalganın tam bir ileri-geri yansıma döngüsünü tamamlaması için toplam mesafe (2 × yay boyu) kadar hareket gerekiyor.
- 1 birim mesafeyi 1 saniyede alıyorsa, yay boyu örnek olarak 6 birimse, dalganın gidip geri dönmesi için 6 + 6 = 12 birim yol alması gerekir.
- Bu durumda 12 saniyede ilk hale döner.
Sorudaki senaryoda, bu mantıkla “12 saniye sonra” sonucu verilmiş olabilir. Elinizdeki diyagrama bakarak, dalganın başlangıç ve bitiş noktasına kadar izlediği yolu sayarak kesin değere ulaşabilirsiniz.
4) Doğrusal Dalganın Engelden Yansıması
Sorunun son kısımlarında doğrusal dalga bir engelle karşılaştığında, yansıma açısı ve geliş açısıyla ilgili durum soruluyor. Temel kuralımız şudur:
- Yansıma Yasası: Düz bir engelden yansıyan dalganın geliş açısı (θ_i) ile yansıma açısı (θ_r) birbirine eşittir. Formül:\theta_i = \theta_rBurada açı, engel yüzeyine dik olan normale göre ölçülür.
Eğer dalga 30°’lik veya 40°’lik bir açıyla engelle karşılaşıyorsa, yansıyan dalga da aynı açıyla ama simetrik tarafta yansıyacaktır. Soruda, “Şekildeki doğrusal dalganın 40° açıyla geldiği gözleniyor ve 40° açıyla yansır” veya “30° açıyla geliyorsa yine 30° ile yansır” gibi açıklamalar yapılmıştır. Bu da geliş doğrultusunun normalle yaptığı açının korunması demektir.
5) Özet ve Önemli Noktalar
- Sabit Uç: Ters yansıma (baş yukarı → baş aşağı).
- Serbest Uç: Doğrudan yansıma (baş yukarı → baş yukarı).
- K, L, M Noktaları: Dalganın ilerlediği yönde (ok yönünde) hareket eder.
- Zaman Hesabı: Atmanın aynı konum ve faz hâline gelmesi için gereken süre, dalganın tam tur (gidip dönme veya periyodik) hareket süresine eşittir.
- Engelden Yansıma: “Gelen açı” = “Yansıma açısı”; bu dalga davranışı ışık dalgaları için de geçerlidir.
Aşağıdaki tabloda, bu maddeleri kısaca özetleyebilirsiniz:
| Konu | Açıklama |
|---|---|
| Sabit Uçtan Yansıma | Dalganın fazı 180° ters döner (tepe → çukur). |
| Serbest Uçtan Yansıma | Dalganın fazı korunur (tepe → tepe). |
| K, L, M Noktalarının Hareket Yönleri | Dalga hangi yönde ilerliyorsa, K, L, M de o yönde ilerler (ok yönünde). |
| Aynı Konum & Faz Süresi | Dalga ileri-geri hareketi tamamlayınca, 12 s gibi bir zamanda eski haline döner. |
| Doğrusal Dalganın Engelden Yansıması | Geliş açısı = Yansıma açısı; 30° ile gelen 30° ile, 40° ile gelen 40° ile yansır. |
Bu tablonun yanı sıra detaya girerek tekrar hatırlatmak gerekirse, dalga mekaniğinde serbest ve sabit uçtan yansıma prensiplerini ve açıların nasıl korunduğunu anlamak, sorudaki tüm alt maddeleri çözümlemede yeterli olmaktadır.