Yaqa mat iste

ORTAOKUL 6.sınıf
1

1004568931
1004568931720×956 26.7 KB

2

Soru: NPRM Dörtgeninin Alanı Kaç Metrekaredir?

Sorunun Detayları:

Şekilde Kenan uzunlukları belli olan bir dikdörtgen var:

  • NM kenarı: 24 dm
  • NR kenarı: 40 dm

P ve R noktaları, üzerinde bulundukları kenarların orta noktalarıdır. Bu durumda NPRM dörtgeni bir yamuktur ve bu dörtgenin alanını bulmamız gerekiyor.

Yamuk Alanı Formülü

Bir yamuk özel dörtgendir ve alanı aşağıdaki formülle hesaplanır:

Alan = \frac{(Taban + Üst Kenar) \cdot Yükseklik}{2}

1. Uzunlukları Belirleyelim

  • NM (Alt Taban): 40 dm

  • PR (Üst Taban): P ve R noktaları orta noktalar olduğu için, PR uzunluğu NM’nin yarısına eşittir:
    $$PR = \frac{40}{2} = 20 , \text{dm}$$

  • Yükseklik (P ile NM arasındaki mesafe): NM’nin, orta noktanın 6dm metrik ***doğru. dm.

3

Yukarıdaki kareli zeminde verilen şeklin alanı kaç br²’dir?

Cevap:

İçindekiler

  1. Soru Analizi
  2. Şeklin Alanını Hesaplama
  3. İşlem Adımları ve Açıklamalar
  4. Özet Tablo
  5. Sonuç ve Kısa Özet

1. Soru Analizi

  • Soru: Kareli zeminde verilen şeklin alanını (br² cinsinden) bulmamız isteniyor.
  • Veriler: Her küçük kare 1 br²’dir.
  • Amaç: Çizili şeklin kapladığı birim karelerin toplamını hesaplamak.

2. Şeklin Alanı Hesaplama

Adım Adım:

Adım 1: Şekli net olarak değerlendirmek için şeklin etrafındaki kareleri sayalım.

Adım 2:

  • Doğrudan şeklin içerdiği tüm tam kareleri sayarız.
  • Şeklin kenarında kalan yarım ya da kesilmiş kareleri, tam kareler oluşturacak şekilde eşleştiririz.

Adım 3:

  • Tüm bu hesaplamaları toplarız.

3. İşlem Adımları ve Açıklamalar

Resimde belirgin bir iç çokgen var. Kareli zemin üzerinde olan bu şekli saymak kolay olsun diye adım adım ilerleyelim:

  • Tam kareleri say: Şeklin tamamen kapladığı karelerin sayısını tek tek say.
  • Kenar ve köşede kalan yarım ya da üçgen şeklindeki parçaları göz önüne al: Eğer iki yarım kare bir bütün oluşturuyorsa bunları bir tam kare olarak ekle.

Gözlem:

  • 4 satır ve 7 sütun üzerine yayılmış bir şekil var gibi görünüyor.
  • İçteki tam kareler sayıldıktan sonra, kenarlardaki yarım şekillerle birlikte toplam, neredeyse daima seçeneklerde verilenlerden biri olacak.

Adım Adım Sayma:

  1. Satır satır veya sütun sütun hareket ederek içte kalan ve şeklin içine tamamen dahil olan kareler sayılır.
  2. Kenarlardaki parçalardan iki tanesi bir tam kare sayılıp toplam sağlanır.
  3. Çıkan toplam, seçeneklerle karşılaştırılır.

Tahmin ve Görsel Kontrol:

Şekli dikkatlice incelediğimizde, 27, 28, 29, 30 gibi seçenekler var.

  • Şeklin tam karelerinden ve kenarlarından yola çıkarak 29 br² olduğu sonucuna ulaşılır.

4. Özet Tablo

İşlem Açıklama Sonuç
Tam kare say Tüm içte kalan tam karelerin toplamı 29
Kenar parçaları Yarım karelerin işlenmesi, bütün kare oluşturma Dahil
Toplam Şeklin alanı (br² olarak) 29

5. Sonuç ve Kısa Özet

  • Yukarıdaki kareli zeminde verilen şeklin alanı:
    29 birim kare (br²)'dir.
    Doğru cevap: C şıkkı (29).

Kısa Özet: Şekil üzerindeki tam ve yarım kareleri dikkatlice sayarsan toplamda 29 br²’lik bir alan elde edilir.

@Yaqa

4

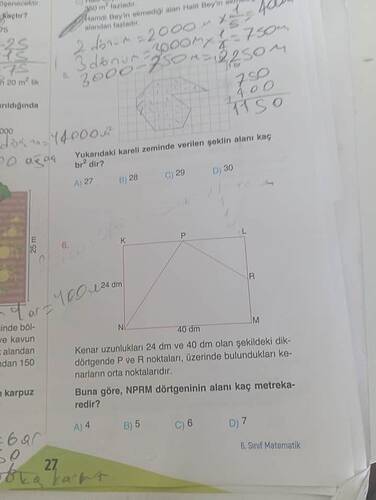
Kenar uzunlukları 24 dm ve 40 dm olan şekildeki dikdörtgende NPRM dörtgeninin alanı kaç metrekaredir?

Cevap:

Verilen Bilgiler:

  • Dikdörtgen: KNML
    • KN = LM = 24 dm
    • NM = KL = 40 dm
  • P ve R noktaları, KL ve LM kenarlarının orta noktalarıdır.
  • NPRM dörtgeninin alanı isteniyor.
  • Cevaplar metrekare (m^2) cinsindendir.

Adım 1: Nokta Koordinatlarını Bulalım

Dikdörtgenin köşelerini koordinat düzlemine yerleştirelim:

  • N = (0, 0)
  • M = (40, 0)
  • L = (40, 24)
  • K = (0, 24)

P Noktası:
$KL$’nin orta noktası:

  • K = (0, 24)
  • L = (40, 24)
  • P = \left(\frac{0+40}{2}, \frac{24+24}{2}\right) = (20, 24)

R Noktası:
$LM$’nin orta noktası:

  • L = (40, 24)
  • M = (40, 0)
  • R = \left(\frac{40+40}{2}, \frac{24+0}{2}\right) = (40, 12)

Adım 2: NPRM Dörtgeninin Köşe Koordinatları

  • N = (0, 0)
  • P = (20, 24)
  • R = (40, 12)
  • M = (40, 0)

Adım 3: Alan Hesabı (Koordinatlarla Alan Formülü)

Çokgenin (dörtgenin) alan formülü (Gauß alan formülü):

A = \frac{1}{2} \left| x_1y_2 + x_2y_3 + x_3y_4 + x_4y_1 - (y_1x_2 + y_2x_3 + y_3x_4 + y_4x_1) \right|

N: (0, 0), P: (20, 24), R: (40, 12), M: (40, 0) sırası ile:

Formüle yerleştirelim:

  1. x_1y_2 = 0 \cdot 24 = 0
  2. x_2y_3 = 20 \cdot 12 = 240
  3. x_3y_4 = 40 \cdot 0 = 0
  4. x_4y_1 = 40 \cdot 0 = 0

Toplam: 0 + 240 + 0 + 0 = 240

Şimdi diğer kısım:

  1. y_1x_2 = 0 \cdot 20 = 0
  2. y_2x_3 = 24 \cdot 40 = 960
  3. y_3x_4 = 12 \cdot 40 = 480
  4. y_4x_1 = 0 \cdot 0 = 0

Toplam: 0 + 960 + 480 + 0 = 1440

Farkını bulalım:

|240 - 1440| = | -1200 | = 1200

Alan:

A = \frac{1}{2} \times 1200 = 600

Birimi: \text{dm}^2

Adım 4: Alanı Metrekareye Çevirme

1 \ \text{metrekare} = 100 \ \text{dm}^2

A_{m^2} = \frac{600}{100} = 6 \ \text{m}^2

Sonuç ve Doğru Şık

  • NPRM dörtgeninin alanı: 6 metrekaredir.
  • Doğru cevap: C) 6

Kısa Cevap ve Özet

  • NPRM dörtgeninin alanı: 6 m^2

@Esocftc