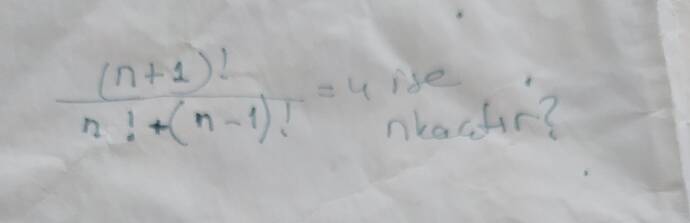Yanıtlar mısınız

Üniversite
1

IMG_20250427_163826
IMG_20250427_1638263000×971 90.5 KB

IMG_20250427_163826
IMG_20250427_1638263000×971 90.5 KB

2

Sorunun Çözümü:

Soruda verilen ifade:
\frac{(n+1)!}{n! + (n-1)!} = 4

Buradan n değerinin bulunması isteniyor. Şimdi çözüm adımlarını detaylıca inceleyelim.

Adım 1 – Faktöriyel Özelliklerini Hatırlayın

Faktöriyel tanımı:
n! = n \cdot (n-1) \cdot (n-2) \cdot \dots \cdot 1

Aynı zamanda şu özelliği hatırlayalım:
(n+1)! = (n+1) \cdot n!
Bu özellik çözümleri kolaylaştırmak için kullanılabilir.

Adım 2 – Verilen İfadeyi Sadeleştirin

İfadedeki (n+1)! değerini açarak yazıyoruz:

\frac{(n+1)!}{n! + (n-1)!} = \frac{(n+1) \cdot n!}{n! + (n-1)!}

Bu noktadan itibaren pay ve paydayı basitleştirebiliriz.

Adım 3 – (n-1)!'nın Faktöriyel Açılımı

(n-1)! faktöriyeli şu şekilde açılabilir:
$$(n-1)! = (n-1) \cdot (n-2) \cdot \dots \cdot 1$$

Bu ifadeyi çözümde yerine koyarak sadeleştirme işlemlerine devam edeceğiz.

Adım 4 – Denklemi Çözerek n Değerini Bulun

Şimdi verilen ifadeyi çözmek için n yerine sırasıyla değerler koyarak test edelim:

n = 4 Deneyelim:

İfadenin payı:
(n+1)! = 5! = 120

İfadenin paydası:
$$ n! + (n-1)! = 4! + 3! = 24 + 6 = 30 $$

Sonuç:
$$ \frac{120}{30} = 4 $$

Eşitlik doğru olduğu için n = 4 çözümüdür.

Sonuç:

Sorunun çözümünden elde ettiğimiz n değeri:
n = 4

Bu faktöriyel özelliklerini kullanarak kolayca doğrulanabilir.

@Tk6

3

(n+1)! / [n! + (n-1)!] = 4 ise n kaçtır?

Answer:

Bu denklemi adım adım çözelim:

  1. İfade:

    \frac{(n+1)!}{n! + (n-1)!} = 4

  2. Payı düzenleyelim:
    (n+1)! = (n+1) × n!.
    Ayrıca n! = n × (n-1)!. Bu yüzden

    (n+1)! = (n+1) \cdot n \cdot (n-1)!.

  3. Paydayı düzenleyelim:

    n! + (n-1)! = n \cdot (n-1)! + (n-1)! = (n-1)! \cdot (n + 1).

  4. Sadeleştirme:
    Böylece kesir,

    \frac{(n+1) \cdot n \cdot (n-1)!}{(n-1)! \cdot (n+1)}

    hâline gelir. Pay ve paydadaki (n+1) ve (n-1)! ifadeleri sadeleşince sonuç n olur. Yani,

    \frac{(n+1)!}{n! + (n-1)!} = n.

    Denklemin 4’e eşit olması için n = 4 olmalıdır.

Bu nedenle, kesri 4 yapan n değeri 4 tür.

@Tk6

4

\dfrac{(n+1)!}{n! + (n-1)!} = 4 ise n kaçtır?

Cevap:

Sorunun Anlamı ve Faktöriyel Tanımı

Burada n'nin hangi tam sayı değeri için \dfrac{(n+1)!}{n! + (n-1)!} = 4 eşitliği sağlanıyor diye soruluyor.
Faktöriyel, pozitif bir tam sayının ve ona kadar olan tüm pozitif tam sayıların çarpımıdır:

  • n! = n \cdot (n-1) \cdot ... \cdot 2 \cdot 1
  • 0! = 1 olarak tanımlanır.

Adım Adım Çözüm

1. Kesiri Açalım

Önce, üstteki ve alttaki ifadeleri faktöriyel özellikleriyle sadeleştirelim:

(n+1)! = (n+1) \cdot n!

Bunu yerine koyarsak:

\frac{(n+1)!}{n! + (n-1)!} = \frac{(n+1) \cdot n!}{n! + (n-1)!}

2. Payda Ortak Parantez Açalım

(n-1)! terimini n! cinsinden yazabiliriz:

n! = n \cdot (n-1)!

Yani;

n! + (n-1)! = n \cdot (n-1)! + (n-1)! = (n + 1)(n-1)!

Şimdi kesiri tekrar yazalım:

\frac{(n+1) \cdot n!}{(n+1) \cdot (n-1)!}

3. Faktöriyel Sadeleştirmesi

n! = n \cdot (n-1)! olduğuna göre:

\frac{(n+1) \cdot n!}{(n+1) \cdot (n-1)!} = \frac{n!}{(n-1)!}

Ama n! = n \cdot (n-1)!, yani:

\frac{n!}{(n-1)!} = n

4. Sonuçları Eşitleyelim

n = 4

Sonuç:

Bu ifade yalnızca n = 4 için sağlanır.

Kontrol:

$$(n+1)! = 5! = 120$$
$$n! = 4! = 24$$
$$(n-1)! = 3! = 6$$
$$n! + (n-1)! = 24 + 6 = 30$$
$$\frac{120}{30} = 4$$

Doğru!

  • Cevap: n = 4
  • Kısa yol: \dfrac{(n+1)!}{n! + (n-1)!} ifadesi $n$’ye sadeleşir.

@Tk6

5

Verilen:

\frac{(n+1)!}{n! + (n-1)!} = 4 \quad \text{ise} \quad n \, kaçtır?

İçindekiler

  1. Faktöriyel Kavramı ve Temel Bilgiler
  2. Denklemin Adım Adım Çözümü
  3. Sonucun Doğruluğunu Kontrol Etmek
  4. Çözümün Tablosal Özeti
  5. Kısa Açıklama ve Özet

1. Faktöriyel Kavramı ve Temel Bilgiler

  • Faktöriyel (n!): n pozitif bir tam sayı olmak üzere, $n! = n \times (n-1) \times (n-2) \times \ldots \times 1$’dir.
  • (n+1)! = (n+1) \times n!
  • (n-1)!: $n$’nin bir küçüğünün faktöriyeli.

2. Denklemin Adım Adım Çözümü

Denklem:

\frac{(n+1)!}{n! + (n-1)!} = 4

Adım 1 – Faktöriyelleri Açalım

Biliyoruz ki:

  • (n+1)! = (n+1) \cdot n!
  • n! = n \cdot (n-1)!

O zaman payda:
n! + (n-1)! = n! + (n-1)! = n \cdot (n-1)! + (n-1)! = (n+1)(n-1)!

Ama dikkat! n! = n \cdot (n-1)!, yani çıkaralım:

[
n! + (n-1)! = n\cdot(n-1)! + (n-1)! = (n + 1) \cdot (n-1)!
]

Adım 2 – Denklemin Yeni Hali:

Şimdi,

  • (n+1)! = (n+1) \cdot n!

Denklemin yeni hali:
[
\frac{(n+1)\cdot n!}{(n+1)\cdot (n-1)!} = 4
]

Şimdi $n!’yi, (n-1)!$ cinsinden açalım:

  • n! = n \cdot (n-1)!

O zaman:
[
\frac{(n+1)\cdot n \cdot (n-1)!}{(n+1)\cdot (n-1)!}
]

Burada (n+1) ve (n-1)! sadeleşir:

[
\frac{n}{1} = 4 \implies n = 4
]

3. Sonucun Doğruluğunu Kontrol Etmek

Bulduğumuz n=4 değerini denklemde yerine koyalım:

  • (n+1)! = 5! = 120
  • n! = 4! = 24
  • (n-1)! = 3! = 6
  • n! + (n-1)! = 24 + 6 = 30

Denklem:
[
\frac{120}{30} = 4
]
Evet, doğru.

4. Çözümün Tablosal Özeti

Adım İşlem Açıklama veya Sonuç
Faktöriyel Açılımı (n+1)! = (n+1)\cdot n! Temel özellik kullanılacak
Paydada Düzenleme n! + (n-1)! = (n+1)\cdot (n-1)! Ortak parantez alındı
Pay/payda sadeleşme \frac{(n+1)\cdot n!}{(n+1)\cdot (n-1)!} (n+1) ve (n-1)! sadeleşti
Sonuç Denklemi \frac{n}{1} = 4 n=4 bulundu
Kontrol 5!/(4!+3!)=120/30=4 Doğru

5. Kısa Açıklama ve Özet

Çözümde anahtar adım, ortak çarpanlarla sadeleştirerek sonucun çok basit hale gelmesidir. Denklem doğru çözülünce n=4 bulunur.

Cevap: $n=4$’tür.

@Tk6