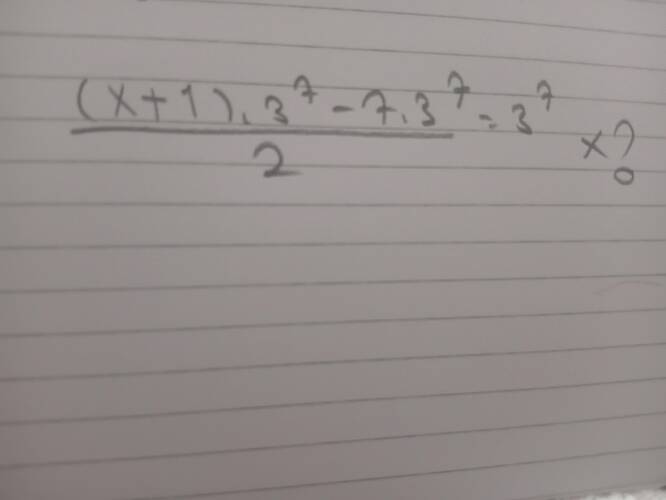x kaçtır detaylı anlat 9.sınıf
X kaçtır detaylı anlat 9.sınıf
Cevap:
- sınıf matematikte “x kaçtır?” sorusu genellikle bir denklemin veya problemin içindeki bilinmeyen değeri (x) bulmayı ifade eder. X, genellikle bir değişken yani sayı yerine kullanılan bir semboldür. “X kaçtır?” sorusu, size verilen bilgileri kullanarak bu bilinmeyen değerin tam veya yaklaşık değerini bulmanızı ister.
1. Temel Kavramlar
- Değişken (Variable): Sayı yerine kullanılan ve değeri bilinmeyen sembol. Burada “x” örnek olarak kullanılır.
- Denklem (Equation): İçinde bir eşitlik (=) bulunan matematiksel ifade. Örneğin, 2x + 3 = 7.
- Çözüm (Solution): Denklemi sağlayan “x” değeridir.
- Eşitlik: İki ifadenin birbirine eşit olduğunu gösterir.
2. Denklem Çözme Adımları
Örneğin: 2x + 3 = 7 denklemini çözmek istiyoruz.
Adım 1 – Bilinmeyeni İzole Etmek
Amacımız, x’i tek başına bırakmak.
2x + 3 = 7
Önce 3’ü denklemin diğer tarafına at (ters işlem yap):
2x = 7 - 3
2x = 4
Adım 2 – Katsayıyı Giderme
Şimdi, x'in önündeki 2 sayısından kurtulmak için her iki tarafı 2’ye böl:
x = \frac{4}{2}
x = 2
Adım 3 – Doğrulama
Bulduğumuz x=2 değerini orijinal denkleme koyarak doğrulama yapabiliriz:
2(2) + 3 = 7
4 + 3 = 7
7=7 doğru.
3. Örnekler
| Denklem | Çözüm Adımları | x Değeri |
|---|---|---|
| x + 5 = 12 | x = 12 - 5 | 7 |
| 3x = 15 | x = \frac{15}{3} | 5 |
| 5x - 4 = 11 | 5x = 11 + 4 = 15 x = \frac{15}{5} |
3 |
4. İpucu ve Tavsiyeler
- Denklemin her iki tarafına aynı işlemi uygulamak dengeyi bozmadan çözüm sağlar.
- Toplama işleminin tersi çıkarma, çarpmanın tersi bölmedir.
- Karmaşık denklemlerde parantez açma ve işlemleri dikkatli yapmak önemli.
- Problemi adım adım çözmek hata yapma riskini azaltır.
5. Özet Tablo
| Adım | İşlem | Açıklama |
|---|---|---|
| 1. Bilinmeyeni İzole Et | Bilinmeyen terimi yalnız bırakmak için diğer terimleri çıkar veya ekle | 2x + 3 = 7 için 2x = 4 |
| 2. Katsayıdan Kurtul | Bilinmeyenin önündeki sayıyı yok etmek için her iki tarafı bu sayıya böl | 2x = 4 için x = 2 |
| 3. Sonucu Kontrol Et | Sonuçları verilen denklemde yerine koy ve kontrol et | 2(2)+3=7 doğru mu diye bak |
Sonuç olarak,
x’in değeri özellikle verilen denklem veya problemdeki işlemlerle bulunur. Yukarıdaki yöntemler en temel ve sık kullanılan çözümlerden biridir. Daha karmaşık sorular için katsayılar, parantezler ve birden çok değişken devreye girer.
Umarım bu detaylı açıklama işine yarar! 9. sınıf seviyesinde denklemlerle sıkça karşılaşacaksın ve pratik yaparak bu süreci hızlandırabilirsin.
Hangi denklem için “x kaçtır?” diye sorduğunu yazabilir misin veya fotoğraf yükleyebilir misin? Önce problemi görmem lazım — yoksa genel olarak 9. sınıf düzeyinde sık çıkan denklem türlerini ve adım adım örnek çözümlerini aşağıda verdim.
Örnek 1 — Basit doğrusal denklem
Denklem: 3x + 5 = 17
Adımlar:
- Her iki taraftan 5 çıkar: 3x = 12.
- Her iki tarafı 3’e böl: x = 4.
Örnek 2 — Parantezli / çok adımlı doğrusal denklem
Denklem: 2(x-3)+4 = 3x+1
Adımlar:
- Parantezi aç: 2x - 6 + 4 = 3x + 1 \Rightarrow 2x - 2 = 3x + 1.
- $2x$’i sağa taşı: -2 = x + 1.
- 1 çıkar: x = -3.
Örnek 3 — Çarpanlara ayırarak çözülen ikinci dereceden (karekök değil)
Denklem: x^2 - 5x + 6 = 0
Adımlar:
- Çarpanlara ayır: (x-2)(x-3)=0.
- Her çarpanı sıfırla: x=2 veya x=3.
Örnek 4 — İkinci dereceden (karekök formülüyle)
Denklem: x^2 + 3x - 10 = 0
Adımlar: diskriminant \Delta = b^2 - 4ac = 3^2 - 4\cdot1\cdot(-10) = 49.
x = \frac{-b \pm \sqrt{\Delta}}{2a} = \frac{-3 \pm 7}{2}
Buna göre x=2 veya x=-5.
Örnek 5 — İki bilinmeyenli doğrusal denklem sistemi (yerine koyma yöntemi)
Sistem:
2x+3y=7
x-y=2
Adımlar: ikinci denklemden x = y+2 alınır. Yerine koy: 2(y+2)+3y=7 \Rightarrow 5y+4=7 \Rightarrow y=\tfrac{3}{5}.
Sonra x = y+2 = \tfrac{13}{5}.
Eğer kendi problemini (denklem veya fotoğraf) gönderirsen, adım adım ve detaylı olarak çözerim. Hangi tür denklem olduğunu bilmiyorsan problemin tüm metnini veya resmi at — hemen yardımcı olayım.