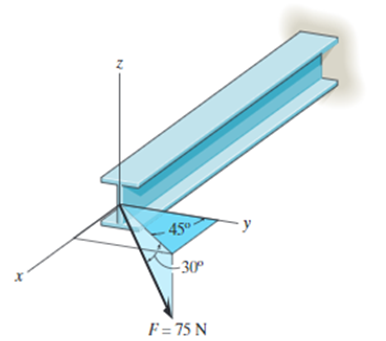
What are the rectangular components of force ( F ) in the given diagram?
Answer:
To determine the rectangular components of the force ( F ) in the given diagram, we need to resolve the force vector into its x, y, and z components. The force ( F ) is given as 75 N, and it’s directed at angles, with respect to the axes, provided in the diagram.
-
Identify Given Angles:
- Angle between the force and the z-axis: (\theta_z = 30^\circ)
- Angle in the x-y plane relative to the x-axis: (\theta_{xy} = 45^\circ)
-
Component in the z-direction (F_z):
F_z = F \cos(30^\circ)
Since ( \cos(30^\circ) = \frac{\sqrt{3}}{2} ),
F_z = 75 \times \frac{\sqrt{3}}{2} = 75 \times 0.866 = 64.95 \, \text{N}
- Magnitude of the force in the x-y plane (F_{xy}):
Since the force makes a 30^\circ angle with the z-axis, the projection in the x-y plane is:
F_{xy} = F \sin(30^\circ)
Since ( \sin(30^\circ) = \frac{1}{2} ),
F_{xy} = 75 \times \frac{1}{2} = 37.5 \, \text{N}
- Component in the x-direction (F_x):
Given the angle in the x-y plane with respect to the x-axis is ( \theta_{xy} = 45^\circ ):
F_x = F_{xy} \cos(45^\circ)
Since \cos(45^\circ) = \frac{\sqrt{2}}{2},
F_x = 37.5 \times \frac{\sqrt{2}}{2} = 37.5 \times 0.707 = 26.52 \, \text{N}
- Component in the y-direction (F_y):
F_y = F_{xy} \sin(45^\circ)
Since ( \sin(45^\circ) = \frac{\sqrt{2}}{2} ),
F_y = 37.5 \times \frac{\sqrt{2}}{2} = 37.5 \times 0.707 = 26.52 \, \text{N}
Therefore, the rectangular components of the force ( F ) are:
F_x = 26.52 \, \text{N}
F_y = 26.52 \, \text{N}
F_z = 64.95 \, \text{N}
1 Beğeni