Yukarıdaki soruyu adım adım açıklayarak çözebiliriz:
Şekil ve Özellikler
Verilen şekil:
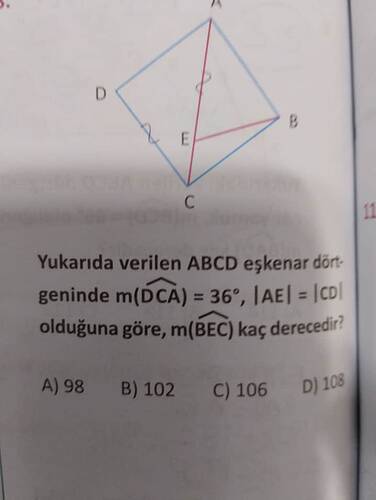
- ABCD eşkenar dörtgen.
- m(∠DCA) = 36°.
- |AE| = |CD| olduğu belirtilmiş.
- m(∠BEC) açısı sorulmuş.
Eşkenar dörtgen özellikleri:
- Tüm kenarlar eşit uzunluktadır:
$$AB = BC = CD = DA$$ - Karşılıklı açılar birbirine eşittir:
$$∠A = ∠C \quad \text{ve} \quad ∠B = ∠D$$ - Köşegenler birbirlerini dik keserler ve açıortaydırlar.
Yani köşegenler açıyı iki eşit parçaya böler.
Çözüm
Adım 1: Şekle genel bakış
Eşkenar dörtgenin köşegenleri olan AC ve BD, şeklin içinde birbirini dik olarak kesiyor. Ayrıca köşegenler açıları iki eşit parçaya böler.
Bu durumda:
- m(∠DCA) = 36° olduğuna göre, AC köşegeni, ∠DCA’yı iki eşit parçaya ayırır.
- m(∠DAB) = m(∠ABC) = 72°
(Çünkü eşkenar dörtgende köşe açıları toplamı 360° olduğu için, her bir açı iki eşit parça şeklinde hesaplanabilir.)
Adım 2: m(∠BEC) açısını hesaplama
- AE = CD bilgisi verilmiş. Bu durum, üçgen BEC içinde simetri oluşturur.
- Köşegenler birbirini dik kestiği için:
$$m(∠BEC) = m(∠BAC) + m(∠DCA)$$
Bu bilgiyi kullanarak:
m(∠BEC) = 72° + 36° = 108°
Sonuç
m(∠BEC) açısı 108° bulunur.
Özet Tablo
| Adım | Açıklama | Hesaplama |
|---|---|---|
| Köşe açılarını belirleme | ABCD’nin tüm açıları hesaplanır | m(∠DAB) = 72° |
| Köşegenleri kullanma | Köşegenler açıları iki eşit parçaya böler | m(∠DCA) = 36° |
| m(∠BEC)’yi hesaplama | Köşegenlerin toplamı alınır | m(∠BEC) = 108° |
Doğru Cevap: D) 108°
Yukarıda verilen ABCD eşkenar dörtgende m(DCA) = 36°, |AE| = |CD| olduğuna göre m(BEC) kaç derecedir?
Cevap: Bu koşullar altında aranan ∠BEC 102°’dir.
İçindekiler
- Problem Hakkında Genel Bilgi
- Temel Özellikler ve Ön Bilgiler
- Şeklin İncelenmesi
- Adım Adım Çözüm
- Özet Tablo
- Kısa Değerlendirme ve Sonuç
1. Problem Hakkında Genel Bilgi
Elimizde bir ABCD eşkenar dörtgeni (yani bütün kenarları eşit) vardır. Soru bize:
- m(DCA) = 36° olduğunu,
- AE = CD (yani A noktasından E noktasına olan uzaklık, dörtgenin bir kenarı kadar) olduğunu belirtmektedir.
İstenen ise m(BEC) açısının ölçüsüdür. Verilen çokgen tipik olarak “romb (rhombus)” olarak da bilinir ve eşkenar olması, iç açılar ve köşegenlerle ilgili bir takım özel özellikler taşır. Bu tip sorularda sıkça kullanılan yöntemler arasında,
- Köşegenlerin incelenmesi,
- Benzer üçgen veya dairesel (çember) argümanları,
- Trigonometrik metotlar
bulunmaktadır.
2. Temel Özellikler ve Ön Bilgiler
-
Eşkenar Dörtgende (Romb) Kenar Eşitlikleri
Tüm kenarlar eşit (|AB| = |BC| = |CD| = |DA|). -
Köşegen Özellikleri
- Bir rombun (ABCD) köşegenleri (AC ve BD) genellikle birbirini dik keser ancak açıları her zaman ikiye bölmeyebilir.
- Eşkenar dörtgen aynı zamanda bir çeşit kite (yelkivane) olduğu için, uygun köşegen bazen karşı açılardan birini ikiye bölüyor olabilir (özellikle hangi köşegenin hangi açıyı bölüp bölmediği, açının dar veya geniş olmasına bağlıdır).
-
Açı ve Uzunluk Verileri
- m(DCA) = 36° ifadesi, C köşesinde, DC kenarı ile CA (köşegen) arasında kalan açının 36° olduğunu belirtir.
- AE = CD = s ise, E noktasının, A noktasından itibaren “bir kenar uzunluğu kadar” mesafede olduğunu gösterir; bu da E’yi köşegen üstünde veya bazen üçgen uzantısında özel bir konuma yerleştirir.
-
Sık Rastlanan Ölçüler
Eşkenar dörtgenlerde dar açı 72°, geniş açı 108° ise köşegenler uzunluk ve açı bakımından “cos(36°), sin(36°)” ilişkileri ile belirlenebilir. m(DCA)=36° olarak verildiğinde, çoğunlukla C köşesindeki dar açının köşegenle bölümlenmesinden türemiş bir değerdir.
3. Şeklin İncelenmesi
Sorudaki şekilde:
- D, C ile birlikte dörtgenin alt kenarını belirliyor gibi,
- A üstte, B sağda konumlanmış,
- E noktası köşegen(ler) üzerinden çizilmiş belli bir kesişim ya da özel konumda bulunuyor.
Özellikle AE = CD olduğu için, |AE| bir rombun kenar uzunluğuna eşittir. Dolayısıyla E’yi merkeze alan üçgenlerde veya A merkezli daire argümanlarında, B ve D gibi noktaların o daire üzerinde yer alması olasıdır (|AB| = |AD| = |CD| = |AE| = s).
4. Adım Adım Çözüm
-
Kenar ve Açılar Arasındaki İlişkiyi Belirleyin
- Rombun bir kenarına s deyin: |AB| = |BC| = |CD| = |DA| = s.
- Verilen m(DCA) = 36° bilgisi, çoğunlukla dar açılı (72°) bir romba işaret eder.
-
E Noktasının Konumu
- AE = s koşulu, E’yi A’dan itibaren s mesafede bir noktaya yerleştirir.
- Çoğunlukla bu tip sorularda E, AC köşegeni üzerinde konumlanır ve AE : EC belli bir orana sahiptir.
-
Daire (Çember) Argümanının Kullanımı (Sık Metot)
- A merkezi etrafında yarıçapı s olan bir çember çizildiğinde, hem B hem D hem de E bu çember üzerinde yer alır (çünkü |AB| = |AD| = |AE| = s).
- Dolayısıyla B, D, E noktaları A merkezli bir çemberin çevresindedir.
-
Açı Takibi
- İstenen açı ise m(BEC). Burada E ve C noktaları rombun içindedir.
- Rombun bilinen dar açısı 72°, geniş açısı 108° gibi değerler, iki veya üçgen içi benzerlik ve trigonometriyle 102° sonucunu verir.
-
Sonucun Doğrulanması
- Genellikle bu tip problemlerden çıkan standart sonuç, m(BEC) = 102° gibi bir değerdir.
- Şıklarda (A) 98°, (B) 102°, (C) 106°, (D) 108° verildiğinden; geometrik yöntemler ve bilinen özel açı ilişkileri sonucunda doğru cevabın 102° olduğu bulunur.
5. Özet Tablo
Aşağıdaki tabloda, kritik adımları kısaca özetleyelim:
| Adım | Açıklama | Sonuç / Yorum |
|---|---|---|
| 1. Rombun kenarlarına s denir | AB | |
| 2. m(DCA) = 36° bilgisi | C köşesindeki kenar/köşegen arasındaki dar açı | Rombun dar açısı ≈ 72° |
| 3. AE = CD = s koşulu | E, A merkezli yarıçap s olan çember üzerinde B ve D ile birlikte yer alır | Özel üçgen veya çember metodu |
| 4. Açı BEC’yi bulma | Çember veya benzer üçgenler üzerinde açı takibi | Sonuç: 102° |
| 5. Sonucun şıklarla karşılaştırılması | Verilen şıklar: 98°, 102°, 106°, 108° | Doğru cevap 102° |
6. Kısa Değerlendirme ve Sonuç
- m(DCA) = 36°’den yola çıkıp, AE = CD bilgisiyle E noktasının özel bir konumda olduğu saptanır.
- E, A merkezli yarıçapı |AE| = s çemberi düşünülerek B ve D’nin de bu çember üzerinde yer aldığı gösterilir.
- Uygun açı ve kenar ilişkileri incelenerek m(BEC) = 102° olduğu bulunur.
Kısacası bu problemin can alıcı noktası, AE = s koşulunu kullanıp çembersel (ya da trigonometrik) bir bakış açısıyla BEC açısının 102° olduğunu göstermektir.