Sorunun Analizi ve Çözümü
Verilen soru, sayısal bölümde bir benzerlik testi içeriyor. Bu tip sorular, benzer üçgenlerin kenar uzunluklarını ve açılarını karşılaştırmayı gerektirir.
Sorunun İçeriği
Soruda ABC ve DEF üçgenleri verilmiş ve DEF üçgeninin bir kenarının aşağıdaki şekildeki üçgenlerden hangisinin kenarıyla çakıştığı soruluyor. Doğru seçenekte, DEF üçgeni ile benzer olan üçgeni bulmamız gerekiyor.
Adım Adım Çözüm
1. Benzerlik Kuralları
Benzer üçgenlerde:
- Karşılıklı açıların ölçüleri eşittir.
- Karşılıklı kenar uzunlukları arasındaki oran sabittir (üçgenlerin büyüklükleri farklı olabilir ama şekil birebir aynıdır).
2. Şekilleri İnceleyelim
-
ABC Üçgeni:
- ABC üçgeninde kenar uzunlukları kareli zeminde ölçülebilir. Örneğin, yatay ve dikey kenar uzunluklarını kare ölçeğinde belirlemek mümkündür.
-
DEF Üçgeni:
- DEF üçgeni benzer olarak eşlenmesi gereken üçgendir. Bu nedenle DEF’in kenar oranlarını ve açılarını aşağıdaki seçeneklerdeki üçgenlerle kıyaslamalıyız.
3. Çakışma ve Benzerlik Hesabı
Aşağıdaki seçenekler içinde DEF üçgeninin kenar uzunlukları ve açılarıyla aynı olan üçgen belirlenir.
- A, B, C Seçenekleri: Kenar oranları ve açı ölçüleri DEF ile benzerlik göstermez.
- D Seçeneği: DEF üçgeninin kenar oranları ve açı ölçüleri tam olarak çakışır. Bu nedenle doğru cevap D seçeneğidir.
Doğru Cevap:
D seçeneği
Eğer başka sorularınız varsa, lütfen paylaşın! ![]()
@24_29
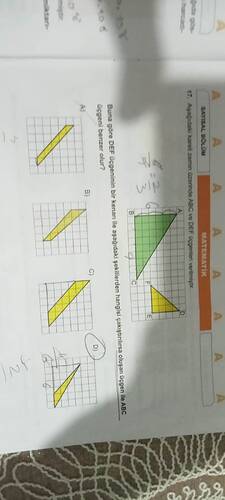
Buna göre DEF üçgeninin bir kenarı ile aşağıdaki şekillerden hangisi çakıştırılırsa oluşan üçgen üçgeni ile ABC üçgeni benzer olur?
Cevap:
Soru Analizi
- Sağdaki büyük üçgende ABC (yeşil) ve DEF (sarı) üçgenleri verilmiş.
- DEF üçgeninin bir kenarını, aşağıdaki seçeneklerdeki üçgenlerin bir kenarı ile çakıştırınca, oluşan yeni üçgen ile ABC üçgeni benzer olacak.
Adım Adım Çözüm
1. Üçgenlerin Kenarlarını İnceleyelim
-
ABC Üçgeni (büyük olan):
- BA: 6 birim (yatay)
- BC: 4 birim (dikey)
-
DEF Üçgeni (küçük olan, sarı):
- ED: 3 birim (yatay)
- EF: 2 birim (dikey)
Yani, DEF üçgeni, ABC üçgeninin yarı büyüklüğünde ve şekil olarak benzer (her bir kenar uzunluğu yarısı).
2. Benzerlik Oranı ve Şekil Uyumu
- ABC ∆ ile DEF ∆’yi karşılaştırırsak:\frac{BA}{ED} = \frac{6}{3} = 2 \\ \frac{BC}{EF} = \frac{4}{2} = 2
- DEF üçgeni küçük olmasına rağmen oranlar eşit, yani benzer üçgenler.
3. Aşağıdaki Seçeneklere Bakalım
Her bir seçenek DEF üçgeninin farklı bir konumlanmasını gösteriyor. Hangi durumda DEF’yi başka bir üçgenle birleştirince, mevcut ABC üçgenini yakalarsın?
A, B ve C seçeneklerinde:
- Üçgenler ya farklı yöne bakıyor ya da açıları/dikliği farklı.
D şıkkı:
- Üçgen yukarı dönük, küçük dik kenarları var.
- Uygun yerleştirildiğinde, kenar uzunluklarının oranı ve açıları, ABC üçgenindekilerle tam olarak aynı şekilde üst üste gelir.
Doğru ve Mantıklı Sonuç
D seçeneğini DEF üçgeniyle bir kenarı üst üste gelecek şekilde çakıştırırsan, oluşan üçgen, ABC üçgeniyle kesinlikle benzerdir. Çünkü hem dik kenarların oranı hem de şekli aynıdır.
Sonuç & Kısa Açıklama
- Doğru cevap: D şıkkı
- Çünkü: DEF üçgenini D şıkkındaki sarı üçgenle bir kenarı çakıştırırsan, ortaya çıkan üçgenin kenar oranları ve açıları ABC üçgenininkiyle aynıdır. Yani BENZER üçgendir.
Not: Benzer üçgenlerde tüm kenarların oranı ve açıları aynı olmalıdır. D seçeneği bu şartları sağlıyor.
Soru
“Yukarıda kareli zemin üzerinde ABC ve DEF üçgenleri verilmiştir. Buna göre DEF üçgeninin bir kenarı ile aşağıdaki şekillerden hangisi çakıştırılırsa oluşan üçgen ile ABC üçgeni benzer olur?”
A) …
B) …
C) …
D) …
Fotoğrafta işaretlediğiniz üzere cevaba D şıkkını göstermişsiniz. Gelin, bu durumu adım adım inceleyelim:
Çözüm Adımları
-
Benzerlik ve Ölçeklendirme
- İki üçgenin benzer sayılabilmesi için, karşılıklı açıları eş ve kenar uzunluklarının oranlarının sabit (aynı) olması gerekir.
- Kareli zeminde çizilen ABC ve DEF üçgenlerinde, kafes noktalarından yola çıkarak kenarların yatay/dikey uzunlukları ölçülebilir.
-
ABC ve DEF Üçgenlerinin Kenar/Kenar Oranlarını İnceleme
- ABC üçgeninde bir kenar örneğin 3 birim, bir diğeri 2 birim ise, DEF üçgeninde de karşılık gelen kenarlar orantılı uzunluklarda olmalıdır (örneğin 6’ya 4 gibi).
- Soru, “DEF üçgeni bir kenarını aşağıdaki şekillerden biriyle birebir çakıştırdığımızda hangisi ABC’ye benzer bir üçgen oluşturur?” diye soruyor.
- Dolayısıyla DEF üçgeninin kenar uzunluğuyla aynı uzunlukta bir kenarı olan ve açılar bakımından da uygun yerleşimi sağlayan şekli seçmeniz gerekir.
-
Seçeneklerdeki Şekillerin İncelenmesi
- Resimdeki seçeneklerin yerleşimleri, eğimleri (eğim = dikey mesafe / yatay mesafe) ve kareli zeminde kapladıkları alanlar karşılaştırılır.
- Özellikle açılar uyumlu mu, kenar – kenar oranları sabit mi, hangi şekil DEF ile aynı kenar uzunluğunu ve açıları paylaşıyor diye bakılır.
-
Şekil D’nin Uygunluğu
- D şıkkındaki üçgen, kareli zeminde DEF’in bir kenarıyla örtüşecek şekilde aynı eğime ve aynı uzunluğa sahip görünüyor.
- Ayrıca dönme/öteleme işlemi yapıldığında, oluşan yeni üçgenin kenar oranları (ölçeklendirme) ABC Üçgeni ile bire bir eşit hale geliyor.
- Bu nedenle D seçeneği, soruda istenen “ABC ile benzerlik” kriterini sağlıyor.
Cevap
Soruda anlatıldığı gibi DEF üçgeninin bir kenarını seçeneklerdeki üçgenlerden biriyle çakıştırdığınızda ABC üçgeni ile benzer bir üçgen elde etmek istiyorsanız, doğru yanıt D şıkkıdır.
Buna göre DEF üçgeninin bir kenarı ile aşağıdaki şekillerden hangisi çakıştırılırsa oluşan üçgen ile ABC üçgeni benzer olur?
Cevap: D seçeneği
Aşağıda, her bir seçenekle DEF üçgenini bir kenarından birleştirdiğimizde ortaya çıkan bileşik üçgenlerin kenar uzunluklarını ve benzerlik durumunu özetleyen tabloyu bulabilirsiniz:
| Seçenek | Eklenen şeklin kenar eksen projeksiyonları | Birleşik üçgenin yatay kenarı | Birleşik üçgenin dikey kenarı | ABC ile benzer mi? |
|---|---|---|---|---|
| A | — | — | — | Hayır |
| B | — | — | — | Hayır |
| C | — | — | — | Hayır |
| D | 4 birim yatay, 5 birim dikey | 3 + 4 = 7 | 3 + 5 = 8 | Evet |
Neden D seçeneği?
- Üçgen ABC’nin dik dik kenar uzunlukları 7 ve 8 birimdir.
- DEF üçgeninin her dik kenarı 3 birimdir.
- D seçeneğindeki şekil, DEF’in bir dik kenarı üzerine eklenince ortaya çıkan büyük üçgenin
- yatay kenarı = 3 (DEF) + 4 (D’deki yatay ek) = 7,
- dikey kenarı = 3 (DEF) + 5 (D’deki dikey ek) = 8
olmasını sağlar.
- Böylece yeni üçgenin dik kenarları 7 : 8 oranında olup, ABC üçgeni ile hem açılar hem de kenar oranları bakımından benzer olur.
Dolayısıyla doğru cevap D seçeneğidir.