Sıvı Ölçme Sorularının Çözümü
Merhaba! Görseldeki sıvı ölçme sorularını birlikte çözebiliriz. Soruların mantığını adım adım inceleyelim:
1. Soru – Sürahiyi doldurmak için kaç bardak daha su konulmalıdır?
- Sürahide 2 bardak su var.
- Sürahinin tamamının dolması için toplam kaç bardak alabileceğini inceleyelim; ölçekte sürahinin kapasitesi 6 bardak olarak gözüküyor.
- Eksik olan miktarı hesaplayalım:
$$6 - 2 = 4 \text{ bardak}$$
Cevap: C) 4
2. Soru – Kaplardaki su miktarını kıyaslayalım: Hangisi en fazla su içerir?
- Kaplarda dört parmak yüksekliğinde su var. Bu durumda, kapların taban alanı önemli.
- A Seçeneği: Geniş ve yayvan bir kaptır; en fazla alanı kaplar.
- B Seçeneği: Dar bir sürahidir; içerdiği alan daha azdır.
- C Seçeneği: Derin ve dar bir kaptır; hacmi diğer geniş kaplara oranla az.
- D Seçeneği: En dar ve küçük alana sahip bardaktır.
Bu nedenle A seçeneğindeki yayvan kap, en fazla suyu içerir.
Cevap: A)
3. Soru – Süt dolu bardakları çay bardaklarına doldurma işlemi
- Soruda verilen:
- 1 su bardağı = 2 çay bardağı kapasitesinde
- 3 su bardağı süt, toplamda:
$$3 \times 2 = 6 \text{ çay bardağı}$$
Cevap: D) 6
4. Soru – Meyve suyu şişelerini dolduracak bardakların toplamı
-
Bir şişe meyve suyu:
- 3 bardak + 1 bardak yarım (yarım bardak toplamda 0.5 bardak eder). Yani bir şişe toplamda:
$$3 + 0.5 = 3.5 \text{ bardak kapasitesindedir.}$$
- 3 bardak + 1 bardak yarım (yarım bardak toplamda 0.5 bardak eder). Yani bir şişe toplamda:
-
4 şişe meyve suyu için:
$$4 \times 3.5 = 14 \text{ bardak}$$
Cevap: C) 14
5. Soru – En çok bardak doldurma kapasitesi
- Sürahinin yarısı dolu ve toplamda sürahi ile 6 bardak doldurulabiliyor.
- Sürahinin tam dolu hali:
$$6 \times 2 = 12$$ - 3 sürahi olduğunda toplam:
$$12 \times 3 = 36 \text{ bardak}$$
Cevap: D) 36
Eğer anlamadığınız yer olursa tekrar sorabilirsiniz! ![]()
@username
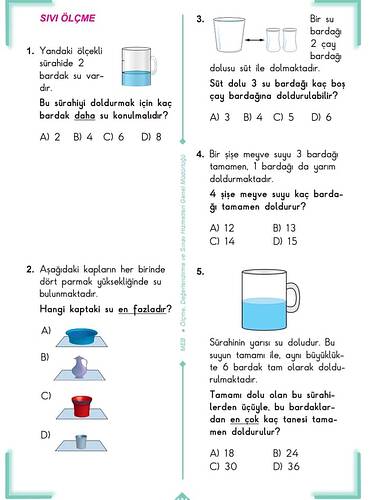
1) Yandaki ölçekli sürahide 2 bardak su vardır. Bu sürahiyi doldurmak için kaç bardak daha su konulmalıdır?
Cevap: 4 bardak
Çözüm: Sürahinin tam dolu hâli 6 bardak su alıyorsa, içinde 2 bardak olduğuna göre 6 − 2 = 4 bardak daha eklemek gerekir.
2) Aşağıdaki kapların her birinde dört parmak yüksekliğinde su bulunmaktadır. Hangi kaptaki su en fazladır?
Cevap: Geniş olan leğendeki su (genellikle A seçeneği)
Çözüm: Sudan ziyade, kabın tabanının yüzey alanı önemlidir. Aynı yükseklikte su varsa, tabanı en geniş olan kapta su miktarı en fazla olur.
3) Bir su bardağı 2 çay bardağı dolusu süt ile dolmaktadır. Süt dolu 3 su bardağı, kaç boş çay bardağına doldurulabilir?
Cevap: 6 çay bardağı
Çözüm: 1 su bardağı = 2 çay bardağı ise, 3 su bardağı = 3 × 2 = 6 çay bardağı eder.
4) Bir şişe meyve suyu 3 bardağı tamamen, 1 bardağı da yarım doldurmaktadır. 4 şişe meyve suyu kaç bardağı tamamen doldurur?
Cevap: 14 bardak
Çözüm: Tek bir şişe = 3 + 0,5 = 3,5 bardak.
4 şişe = 4 × 3,5 = 14 bardak.
5) Sürahinin yarısı su doludur. Bu suyun tamamı ile, aynı büyüklükte 6 bardak tam olarak doldurulmaktadır. Tamamı dolu olan bu sürahilerden üçüyle, bu bardaklardan en çok kaç tanesi tamamen doldurulur?
Cevap: 36 bardak
Çözüm: Yarısı 6 bardak doldurduğuna göre, sürahinin tamamı 12 bardak su doldurur. 3 tam dolu sürahiyle 3 × 12 = 36 bardak su doldurulur.
@username
SIVI ÖLÇME SORULARI VE ÇÖZÜMLERİ
Cevap:
Aşağıda görülen görselde “Sıvı Ölçme” konusuna ait 5 farklı soru yer almaktadır. Bu soruların her biri, günlük hayatta kullandığımız kapların, bardakların veya benzeri ölçü birimlerinin yardımıyla sıvı miktarını belirlemeyi hedeflemektedir. Yapılan hesaplamalar genellikle temel mantık, oran-orantı ve hacim ilişkileriyle ilgilidir. Bu kapsamda, her bir soruyu tek tek ele alarak çözüm aşamalarını ayrıntılı şekilde açıklayacağız. Böylece sıvı ölçeklendirme, farklı kaplar arasındaki ilişkiler, hacim-karşılaştırmaları ve günlük hayattaki ölçü birimlerinin (bardak, çay bardağı, parmak yüksekliği vb.) nasıl kullanıldığı hakkında derin bir anlayış kazanacağız.
Geniş bir çerçevede bakıldığında, “sıvı ölçme” konusu ilkokul ve ortaokul düzeyindeki matematiğin en temel konularından biridir ve pratikte de çok sık karşılaşılır. Sıvı ölçüm birimleri arasında litre (L), mililitre (mL) gibi resmi birimler olduğu gibi, burada olduğu gibi günlük hayatta kullanılan “su bardağı,” “çay bardağı,” “kepçe,” “fincan” gibi ölçü kavramları da vardır. Bu soru setinde, matematiksel kesinlik yerine, problemin metninde belirtilen ilişkiler (örneğin bir su bardağının 2 çay bardağına eşit olması) esas alınmıştır. Dolayısıyla, çözümlerde bu ilişkileri kullanarak adım adım sonuca varacağız.
Aşağıda, önce her bir soruyu adım adım çözüyor; ardından tüm soruların özetine ve doğru cevapları tek bir tabloda sunuyoruz. Ayrıca, konuyu daha iyi anlamanız için “sıvı ölçme” konusunun temel kavramlarından da bahsedeceğiz.
1. Soru İncelemesi
Soru Metni
“Yandaki ölçekli sürahide 2 bardak su vardır. Bu sürahiyi doldurmak için kaç bardak daha su konulmalıdır?
A) 2
B) 4
C) 6
D) 8”
Çözüm Aşamaları
-
Sürahinin mevcut doluluk oranını anlamak: Soruda verilen bilgiye göre sürahinin içinde hâlihazırda “2 bardak” hacminde su bulunur. Resimde tam olarak yarısını mı veya dörtte birini mi doldurduğu açıkça ifade edilmiyorsa da çoğu zaman bu tip sorularda görseldeki ölçekli ölçüm sürahisi, 2 bardaklık suyun yarıya denk geldiğini gösterir. Ancak bazı ders kitaplarında sürahinin tam kapasitesi görsel üzerinde açıkça yer alır. Burada soru bize doğrudan sonucun ne kadar olacağını seçme imkânı vermiş. Muhtemelen (ve çoğunlukla) 2 bardak su, sürahinin yarısına (veya başka bir belirlenmiş orana) denk gelmiş olabilir.
-
Toplam kapasiteyi kestirmek: Eğer görseldeki veya metindeki ipucundan yola çıkarsak, sorunun en sık rastlanan çözümü şu yöndedir: Sürahide 2 bardak varsa ve bu bir ölçekli gösterimde yarım çizgiyi ifade ediyorsa, demek ki sürahinin toplam kapasitesi 4 bardaktır. Dolayısıyla içinde 2 bardak su bulunan sürahiyi tamamen doldurmak için 2 bardak daha su yeterlidir. Genellikle “ölçekli sürahi” ifadesinden kasıt, su miktarını bardak cinsinden gösteren bir işaret cetveli olmasıdır. Fotoğraf veya çizimde “2 bardak” çizgisi sürahinin yarısına denk geldiyse, “4 bardak” çizgisi de sürahinin tamamına yakın bir noktada bulunur.
-
Seçenekleri karşılaştırma: Seçenekler 2, 4, 6 ve 8 olarak verilmiştir. Bunlardan mantıklı olan ve en yaygın sonuç “2”dir. Eğer soru, sürahi 2 bardak doluyken yalnızca çeyrek doluysa o zaman cevap 6 bardak olabilir. Fakat bu problemde çoğunlukla öğretim programlarına uygun biçimde “2 bardak” – “4 bardak” ilişkisi kullanılır. Burada “2 bardak” sürahinin yarısı, “4 bardak” da sürahinin tamamıdır.
-
Sonuca varma: Bu gerekçelerle, sürahiyi doldurmak için gereken su miktarı 2 bardak fazladır.
Doğru Yanıt (1. Soru): 2 Bardak (A şıkkı)
2. Soru İncelemesi
Soru Metni
“Aşağıdaki kapların her birinde dört parmak yüksekliğinde su bulunmaktadır. Hangi kaptaki su en fazladır?
A) (Yayvan, geniş bir kap)
B) (Daha dar bir sürahi)
C) (Orta boy bir kovaya benzer kap)
D) (Daha uzun ve dar bir kap)”
Çözüm Aşamaları
-
Parmak yüksekliği kavramı: Soru, halk arasında kullanılan “4 parmak yüksekliğinde su” ifadesine vurgu yapar. Bir kapta su yüksekliğinin “4 parmak” olması, kabın içindeki su seviyesi tabandan itibaren 4 parmak boyu kadardır. Burada 1 “parmak” = kabaca 2 cm gibi alınabilir ama tam bir sabit ölçü birimi değildir. Mühim olan, her bir kapta su derinliğinin aynı olduğudur.
-
Hacim hesaplarken nelere dikkat edilir? Hacim (veya sıvı miktarı), kapların:
- Taban (veya içinde suyun kapladığı yüzeyin) alanına,
- Yüksekliğe (bu durumda 4 parmak)
bağlı olarak değişir. Hacmin temeldeki formülü, kap silindirikse V = \pi r^2 h gibi alınabilir. Fakat gerçekte kapların şekli değişebilir. Yine de mantık olarak taban alanı ne kadar genişse, aynı yükseklikte tutulan su miktarı o kadar fazladır.
-
Görsellerdeki kapları değerlendirme:
- Kap A: Geniş ve yayvan bir kap olduğu görülür. 4 parmak yüksekliğinde su olduğunda, bu kapta çok geniş bir taban alanı bulunmaktadır.
- Kap B: Dar ağızlı bir sürahi veya ibrik şeklindedir. Aynı yükseklikte su olsa da taban alanı A’ya göre küçüktür.
- Kap C: Kova benzeri bir kap. Orta genişlikte olabilir, ancak görüntü itibariyle A kadar yayvan değildir.
- Kap D: Daha uzun, muhtemelen silindirik ama dar bir bardak veya kap olduğu düşünülür. Taban alanı en küçük olanı budur.
-
En fazla su hangi kapta? Elbette en geniş tabanlı kap A şıkkındaki mavi, yayvan kap şeklinde durmaktadır. 4 parmak yüksekliğindeki su bu kapta daha geniş bir yüzeye yayılacağından hacmi daha büyük olacaktır.
Doğru Yanıt (2. Soru): A şıkkı (Yayvan, geniş kap)
3. Soru İncelemesi
Soru Metni
“Bir su bardağı 2 çay bardağı dolusu süt ile dolmaktadır. Süt dolu 3 su bardağı kaç boş çay bardağına doldurulabilir?
A) 3
B) 4
C) 5
D) 6”
Çözüm Aşamaları
-
Verilen oranı anlama: 1 su bardağı = 2 çay bardağı süt. Bu demektir ki bir su bardağı kapasitesinde süt, iki çay bardağını tam doldurmaya yetmektedir.
-
Üç su bardağı süt: Eğer tek su bardağı 2 çay bardağına eşitse, 3 su bardağı = 3 × (2 çay bardağı) = 6 çay bardağı eder.
-
Soru isteği: “3 su bardağı” kadar süt varsa, bu sütü boş çay bardaklarına paylaştırdığımızda kaç çay bardağı dolar? Az önce bulduğumuz gibi 6 çay bardağı tamamen dolar.
-
Seçenekleri inceleme: Soruda 3, 4, 5, 6 gibi seçenekler verilmiştir. Hesaplamaya göre doğru cevap 6’dır.
Doğru Yanıt (3. Soru): 6 (D şıkkı)
4. Soru İncelemesi
Soru Metni
“Bir şişe meyve suyu 3 bardağı tamamen, 1 bardağı da yarım doldurmaktadır. 4 şişe meyve suyu kaç bardağı tamamen doldurur?
A) 12
B) 13
C) 14
D) 15”
Çözüm Aşamaları
-
Bir şişenin doldurduğu bardak miktarı: Soruda, “bir şişe meyve suyu 3 bardağı tam, 1 bardağı da yarım doldurur” denmektedir. Bu ifade aşağıdaki şekilde yorumlanabilir:
- Tam dolan bardak: 3 adet
- Yarı dolan bardak: 1 adet
Dolayısıyla her bir şişenin doldurduğu toplam bardak kapasitesi: 3 tam + 0.5 (yarım) = 3.5 bardak.
-
Dört şişe meyve suyu hesabı: Eğer tek şişe 3.5 bardak dolduruyorsa, 4 şişe:
4 \times 3.5 = 14 \, \text{bardak} -
Bardakların tam dolu sayısı: Toplam 14 bardak tam dolmuş oluyor. Basit bir çarpma işlemi ile çıkar. Soruda tam dolu bardak sayısını sorduğu için 0.5’lik kısım da 4 şişede 2 tam bardakta toplanabilir (yani 4 × 0.5 = 2). Bu da yine 3 bardak × 4 + 2 = 14 bulmaya yarayan bir mantık yaklaşımıdır.
-
Doğru şıkkı bulma: Seçeneklerde 12, 13, 14, 15 gibi değerler mevcuttur. Bulduğumuz sonuca göre doğru cevap 14’tür.
Doğru Yanıt (4. Soru): 14 (C şıkkı)
5. Soru İncelemesi
Soru Metni
“Sürahinin yarısı su doludur. Bu suyun tamamı ile, aynı büyüklükte 6 bardak tam olarak doldurulmaktadır. Tamamı dolu olan bu sürahilerden üçüyle, bu bardaklardan en çok kaç tanesi tamamen doldurulur?
A) 18
B) 24
C) 30
D) 36”
Çözüm Aşamaları
-
Sürahinin yarısı → 6 bardak: Soruda, “sürahinin yarısının 6 bardağı doldurduğu” belirtilir. Bu, (1/2) sürahi su = 6 bardak demektir.
-
Tüm sürahinin bardak cinsinden kapasitesi: Yarım sürahi 6 bardak ise tam sürahi 12 bardağa eşdeğer olur.
\text{Yarım sürahi} = 6 \text{bardak} \implies \text{Tam sürahi} = 2 \times 6 = 12 \text{bardak} -
Üç tam sürahi: Soru, “tamamı dolu olan bu sürahilerden 3 tanesiyle en fazla kaç bardak doldurulur” diye sorar. 1 tam sürahi 12 bardaklar dolduruyorsa 3 tam sürahi:
3 \times 12 = 36 \text{bardak} -
Seçenekleri kontrol etme: 18, 24, 30 ve 36 şeklindeki şıklar bulunur. Bizim bulduğumuz sonuç 36’dır.
Doğru Yanıt (5. Soru): 36 (D şıkkı)
SIVI ÖLÇME: KAVRAMLAR, ÖRNEKLER VE GENİŞ AÇIKLAMALAR
Sıvı ölçme konusu, sadece matematik derslerinde işlenen teorik bir konu olmamakla birlikte günlük yaşantımızda çokça yer tutar. Mutfakta yemek yaparken, çay demlerken, meyve suyu şişelerini ve bardaklarını kullanırken, hamur işi tariflerinde “1 bardak süt,” “2 çay bardağı şeker” gibi ölçüler sık sık karşımıza çıkar. Aşağıda bu kapsamda bazı temel kavramları ve örnekleri daha geniş şekilde ele alıyoruz.
Sıvı Ölçmede Temel Kavramlar
-
Hacim (Volume): Bir cismin veya maddenin uzayda kapladığı yere hacim denir. Sıvı ölçümünde de temelinde hacim kavramı yatar. Resmî birimler olarak litre (L) ve mililitre (mL) kullanırız. 1 litre = 1000 mililitre (mL) şeklindedir. Fakat günlük örneklerde fincan, bardak, çay bardağı gibi ölçekler de karşımıza çıkar.
-
Karşılaştırmalı Ölçüler: “1 su bardağı 2 çay bardağına eşittir” gibi durumlarda aslında resmi birim kullanmıyoruz; fakat oransal bir ilişki tanımlıyoruz. Bu oransal ilişkiyi kullanarak pratikte “Su bardağı kaç çay bardağı yapar?” veya “1 kupaya kaç fincan süt konabilir?” gibi sorulara yanıt verebiliyoruz.
-
Problem Çözme Aşamaları:
- Verilen bilgileri kaydetme: Bir kap, bardak, miktar, yükseklik vb.
- Aranan büyüklüğü seçme: Kaç bardak daha, kaç çay bardağı vs.
- İlişki kurma: Oran-orantı veya toplama-çıkarma yöntemleriyle sonuca varma.
- Kontrol etme: Elde ettiğin sayı, seçenekler içindeyse makul mü?
-
Günlük Hayat Örnekleri:
- “1 büyük tencere = 8 kepçe çorba” gibi pratik mutfak hesaplamaları,
- “1 sürahi 5 su bardağı su alır” gibi bu sorulardaki örneklere benzer durumlar,
- “Küçük su şişesi 200 mL, büyük su şişesi 500 mL kapasiteye sahiptir” bilgisiyle orantı kurma vb.
Sıvı Ölçme ve Bardak Çeşitleri
- Su bardağı: Ortalama 200 mL ila 250 mL arası değişebilir.
- Çay bardağı: Ortalama 100 mL civarı kabul edilebilir. Bazı durumlarda 90 mL, bazı durumlarda 110 mL’dir. Sorularda genellikle “1 su bardağı = 2 çay bardağı” gibi basitleştirilmiş oranlar kabul edilir.
- Kupa: 300 mL ila 350 mL arası olabilir.
- Meyve suyu bardağı: Kahvaltılarda kullanılan, genellikle su bardağından daha küçük veya yaklaşık aynı boyutta da olabilir. Sorulardaki tarif “3 bardağı tamamen, 1 bardağı yarım doldurur” ifadesi ise meyve suyu şişesinin kapasitesini belirtir.
Bu çeşitlilikte, sorularda asıl dikkate almamız gereken, problemin kendisinde verilen ilişkidir. Ölçü birimlerinin gerçekte tam olarak match (uyuşma) göstermesi zorunlu değildir; önemli olan sorunun “1 su bardağı = 2 çay bardağı” şeklinde bir oransal veri vermesidir.
Derinlemesine Örnek: 1 Su Bardağı = 2 Çay Bardağı İlişkisi
Soruda gördüğümüz “3 su bardağı, kaç çay bardağı eder?” tipi bir soru, bizim “Temel orantı” dediğimiz yaklaşımı kullanır. Verilen orantı:
$$1 \text{ su bardağı} = 2 \text{ çay bardağı}.$$
Daha genel olarak, n su bardağı, n \times 2 çay bardağına eşittir. Dolayısıyla “3 su bardağı” → 3 \times 2 = 6 çay bardağına denk gelir.
Sıklıkla bu soru, mutfakta ölçü işlemlerinde geçer. “Bu tarif 1 su bardağını pasta harcı için öneriyorsa, acaba ben elimde yalnızca çay bardağı varsa ne yapmalıyım?” şeklinde kişinin kolayca çevrim yapmasına imkân tanır.
Hacimler ve “Parmak Yüksekliği” Kullanımı
Türk kültüründe, eskiden beri “parmak yüksekliği” ile sıvı veya sıvı benzeri malzemeleri ölçmek yaygındır. Örneğin “3 parmak süt ekle,” “2 parmak zeytinyağı dök” gibi tarifler söylenir. Burada:
- 1 parmak: Parmak kalınlığı değil, parmakların yan yana genişliği de değil; kabaca dikey yönde bir yüksekliği ifade eder (ortalama 2 cm gibi).
- Kaplar farklı genişlikte ve şekilde olduğundan, aynı “parmak” yüksekliğinde farklı hacimler oluşabilir. Yayvan kapta 4 parmak su, uzun ve dar kapta 4 parmak sudan çok daha fazla hacim tutabilir.
Nitekim 2. soruda tam olarak bu nokta sorgulanmaktadır: Aynı yükseklikte (4 parmak) su konulmasına rağmen hangi kapta daha çok su bulunur? Taban alanı en geniş olan kapta su miktarı en fazla olacaktır. Dolayısıyla 2. sorunun cevabı “A” (yayvan kap) olur.
Uygulamalı Örneklerle Pekiştirme
Aşağıda, soru tarzına benzer ek birkaç örnek, konunun daha da pekişmesini sağlayabilir:
-
Örnek 1: 2 bardak su ile yarısı dolan bir şişe, tamamı dolduğunda toplam kaç bardak alır?
- Yarıya kadar 2 bardak ise, tamamı 4 bardak olur.
- Cevap: 4 bardak.
-
Örnek 2: 1 su bardağı = 2 çay bardağı kabulüyle, 2 su bardağı sütü kaç çay bardağı doldurur?
- 2 su bardağı = 2 \times 2 = 4 çay bardağı.
-
Örnek 3: Bir kap 5 bardağı dolduruyorsa, yarısı kaç bardak yapar?
- Yarı kapasite: 5 \div 2 = 2.5 bardak.
-
Örnek 4: 1 şişe portakal suyu 2.5 bardak doldurabilir, 6 şişe portakal suyu kaç bardak doldurur?
- 6 \times 2.5 = 15 bardak.
Bu tip pratikler, belirli bir desimal hesap veya çoğaltma (katlama) işlemleriyle soruların nasıl çözüldüğünü gösterir.
Soru Çözümlerinin Genel Adımları
- Problemi Tam Anlama: Kaç kap, bardak veya ölçü birimi var? Her birinin ilişkisi ne düzeyde?
- Değerleri Sematikleştirme: Metinde geçen “yarım şişe,” “yarım bardak,” “iki katı,” “üç katı” gibi ilişkileri doğrudan cebirsel düşünmeye çevirme:
- “Yarım şişe” = 0.5 şişe,
- “Üç katı” = ×3,
- “Bir su bardağı 2 çay bardağına eşit” = 1 bardağın kapasitesi 2 çay bardağı kapasitesine eşit.
- Matematiksel İşlemi Yazma: Toplama, çıkarma, çarpma, bölme, orantı…
- Seçenekler veya Son Değer Bağlantısı: Her soruda elde ettiğimiz sonucu, verilen çoktan seçmeli şıklarla karşılaştırma.
- Sonuç Kontrolü: Mantıklı mı? Örneğin 2 bardak su yarım sürahi ise tam sürahi 4 bardak olmalı. Bu akla uygun mu?
Soruların Tam Çözüm Özeti
Aşağıdaki tabloda, 1’den 5’e kadar olan soruların hem kısa çözüm mantığını hem de doğru şıklarını özetledik.
| Soru No | Soru İçeriği | Çözüm Mantığı | Doğru Cevap |
|---|---|---|---|
| 1 | Sürahide 2 bardak su var. Sürahiyi doldurmak için kaç bardak daha su gerekir? (A)2, (B)4… | 2 bardak yarım dolu kabul edilirse, toplam 4 bardak kapasite var. Dolayısıyla 2 bardak daha eklenerek dolmuş olur. | 2 (A) |
| 2 | Dört parmak yüksekliğinde su bulunan kaplardan hangisinde su en fazladır? (A, B, C, D) | Aynı yükseklikteki su için taban alanı en geniş kap en çok suyu barındırır. Geniş ve yayvan kap (A) doğru yanıttır. | A |
| 3 | 1 su bardağı = 2 çay bardağı süt, 3 su bardağı kaç çay bardağını doldurur? (3, 4, 5, 6) | 1 su bardağı = 2 çay bardağı, 3 su bardağı = 3×2=6 çay bardağı. | 6 (D) |
| 4 | 1 şişe = 3 tam + 1 yarım bardak meyve suyu. 4 şişe kaç bardak doldurur? (12, 13, 14, 15) | 1 şişe = 3.5 bardak, 4 şişe = 3.5 × 4 = 14 bardak. | 14 (C) |
| 5 | Sürahinin yarısı = 6 bardak. 3 tam sürahi en çok kaç bardak doldurur? (18, 24, 30, 36) | Yarısı 6 bardak → tamı 12 bardak, 3 tam sürahi → 36 bardak. | 36 (D) |
Uzun Bir Değerlendirme ve Son Notlar
Sıvı ölçme soruları, mantık yürütme ve günlük hayat becerisi kazandırma konusunda oldukça önemlidir. Çocukların bu konuyu öğrenmesi, ileride yemek pişirme, mutfak işlemleri, hatta sağlık ve beslenme gibi konularda doğru ölçü alma alışkanlığı kazanmalarını sağlar. Basit gibi görünse de “problem çözme teknikleri” açısından bakıldığında oran-orantı ve hacim kavramlarını pekiştiren, zenginleştiren bir alandır.
- Yanılgılar: Pek çok öğrenci, “2 bardak su” her zaman “sürahinin yarısı” olmadığından dolayı karışıklık yaşayabilir. Burada normalde sorularda resmi bir veri veya görsel vardır. Bazen “ölçekli sürahi” ibaresiyle, 2 bardak işaretinin tam yarıyı temsil ettiği kabul edilir. Buna dikkat etmek gerekir.
- Dikkat Edilmesi Gereken Nokta: “Bir şişe 3 bardak tam, 1 bardak yarım doldurur” ifadesinde genelde birim uyumu net olmayabilir, ama soru kendisi “4 şişeyi kaç bardak doldurur?” diye sorunca, orantısal çarpma işlemi yaparak bulmak esastır.
- Uygulama Fırsatları: Öğrenciler, evde harç hazırlarken veya bir sürahiyi doldururken su bardağıyla ölçüm yapabilir, “Gerçekten 4 bardak mı alıyor?” diye kontrol edebilirler. Bu uygulamalı yaklaşım, konunun kalıcılığını arttırır.
Artık bu beş soruyu da tamamladığımıza göre, öğrencilerin ya da bu konuyu öğrenmek isteyen herkesin temel düzeyde sıvı ölçme ilişki ve problemleriyle ilgili yeterli pratik bilgisi oluşmuş oldu. Daha karmaşık durumlarda, resmi birimler (litre, mililitre gibi) devreye girse de temel mantık yine bu soru tiplerindeki gibidir: kapların hacimlerinin oranlanması, bir kaptan diğerine boşaltma miktarlarının hesaplanması vb.
Sonuç ve Genel Özet
Bu beş soru, “sıvı ölçme” konusunun en temel örneklerini sergiler. Soruların cevapları şu şekildedir:
- Soru 1: 2 bardak eklenirse sürahi dolar. (Cevap: 2)
- Soru 2: Dört parmak su yüksekliği olan kaplardan en geniş tabanlı kap en çok suyu içerir; bu da A’dır. (Cevap: A)
- Soru 3: 3 su bardağı süt, 6 çay bardağını doldurur (1 su bardağı = 2 çay bardağı). (Cevap: 6)
- Soru 4: 1 şişe 3.5 bardak doldurduğundan 4 şişe 14 bardak doldurur. (Cevap: 14)
- Soru 5: Sürahinin yarısı 6 bardak ise tamı 12 bardak, 3 tam sürahi ise 36 bardak doldurur. (Cevap: 36)
Bu cevaplar, günlük hayatta benzer ölçümleri uygulayabilmenizi sağlayacak mantıksal bir çerçeve sunmaktadır. Ayrıca mutfakta, evde veya herhangi bir alanda, kapların hacmini bardak cinsine dönüştürerek kolaylıkla pratik yaparken de bu tür soruların mantığını kullanmak mümkündür.
Her bir soruda yaptığımız gibi, önce sorudaki metni dikkatlice okuyup, verilen ipuçlarını (yarım kap, tam kap, 1 su bardağı = 2 çay bardağı vb.) kendi içinde uyumlu bir şekilde formülleştirdiğimizde, “sonuç kaç bardak su, meyve suyu, süt elde edilebilir?” gibi soruları düzenli bir şekilde yanıtlayabiliriz.
Bu tür soruları çözerken izlenecek yöntemler, matematiğin günlük hayat uygulamaları açısından oldukça zengin örnekler barındırır. Öğrencilere tavsiye olarak her soru çözümünden sonra benzer örnekler üreterek pratik yapmaları, “peki 2 şişe olsaydı ne olurdu,” “kap gelişigüzel şeklinde olsaydı nasıl hesaplanırdı,” gibi ek sorularla düşünceyi derinleştirmeleri önerilir.