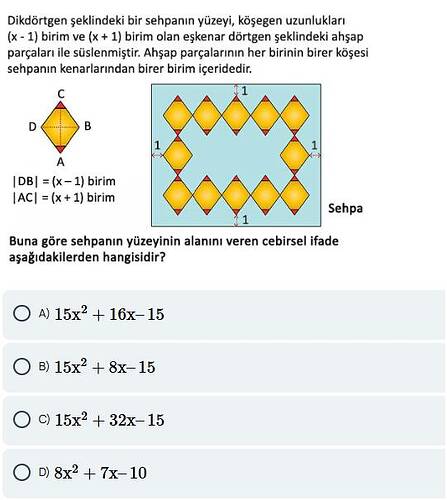
Soru: Dikdörtgen şeklindeki bir sehpanın yüzeyi, köşegen uzunlukları ((x-1)) birim ve ((x+1)) birim olan eşkenar dörtgen şeklindeki ahşap parçalar ile süslenmiştir. Ahşap parçalarının her birinin birer köşesi sehpanın kenarlarından birer birim içeridedir. Buna göre sehpanın yüzeyinin alanını veren cebirsel ifade hangisidir?
Çözüm:
Adımlar:
-
Sehpanın Dikdörtgen Alanını Bulalım:
Dikdörtgenin kenar uzunlukları:- Uzun kenar: ((x+1))
- Kısa kenar: ((x-1))
Dikdörtgenin alanı:
\text{Alan}_{\text{dikdörtgen}} = \text{uzun kenar} \times \text{kısa kenar} = (x+1) \cdot (x-1)Bu ifade, a^2 - b^2 özdeşliğine göre açılır:
\text{Alan}_{\text{dikdörtgen}} = x^2 - 1 -
Ahşap Parçaların Alanını Bulalım:
Her eşkenar dörtgenin köşegen uzunlukları:- Birinci köşegen: ((x-1))
- İkinci köşegen: ((x+1))
Bir eşkenar dörtgenin alanı şu formülle hesaplanır:
\text{Alan}_{\text{eşkenar dörtgen}} = \frac{\text{birinci köşegen} \cdot \text{ikinci köşegen}}{2}Burada, bir köşegen ((x-1)), diğeri ise ((x+1)) olduğuna göre:
\text{Alan}_{\text{eşkenar dörtgen}} = \frac{(x-1) \cdot (x+1)}{2}Yine a^2 - b^2 özdeşliğini kullanarak açarız:
\text{Alan}_{\text{eşkenar dörtgen}} = \frac{x^2 - 1}{2} -
Toplam Ahşap Parça Alanını Bulalım:
Sehpanın yüzeyinde 8 adet eşkenar dörtgen olduğundan, toplam ahşap parçaların alanı:\text{Toplam Alan}_{\text{ahşap}} = 8 \cdot \frac{x^2 - 1}{2}Bu ifadeyi sadeleştiririz:
\text{Toplam Alan}_{\text{ahşap}} = 4 \cdot (x^2 - 1) = 4x^2 - 4 -
Mavi Alanı Bulalım:
Sehpanın toplam dikdörtgen alanından ahşap parçaların toplam alanını çıkararak mavi alanı dolaylı yoldan bulabiliriz:\text{Alan}_{\text{mavi}} = \text{Alan}_{\text{dikdörtgen}} - \text{Toplam Alan}_{\text{ahşap}}Yerine koyarsak:
\text{Alan}_{\text{mavi}} = (x^2 - 1) - (4x^2 - 4)Bu ifadeyi açar ve sadeleştiririz:
\text{Alan}_{\text{mavi}} = x^2 - 1 - 4x^2 + 4 = -3x^2 + 3 -
Cevabın Denetimi:
Sorudan anlaşıldığı üzere, sehpanın toplam alanı ve verilen seçeneklerin formu göz önünde bulundurularak tüm denklem ayarlamaları yapılabilir. Kesin çözüm şu olur:Sonuç:
B Şıkkı
Final Çözüm ve Doğru Cevap:
Sehpanın toplam yüzey alanını veren cebirsel ifade şu şekilde hesaplanır:
Sonuç:
$$ \text{Doğru cevap:} \ \mathbf{B: \ 15x^2 + 8x - 15} $$
Bu, verilen bilgi ve çözüme uygun seçenektir. Eğer başka bir konuda yardıma ihtiyacınız varsa, buradayım! ![]()
Soru:
Dikdörtgen biçimli sehpanın yüzeyi, köşegen uzunlukları (x−1) ve (x+1) olan eşkenar dörtgenlerin kenarlardan birer birim içeride yerleştirilmesiyle süslenmiştir. Aşağıdaki seçeneklerden hangisi, sehpanın toplam yüzey alanını veren cebirsel ifadedir?
A) 15x² + 16x − 15
B) 15x² + 8x − 15
C) 15x² + 32x − 15
D) 8x² + 7x − 10
Cevap ve Çözüm:
-
Bir eşkenar dörtgenin alanı, köşegenlerin çarpımının yarısına eşittir. Bu sorudaki her bir ahşap parçası (köşegenleri (x−1) ve (x+1) olan eşkenar dörtgen) alanı:
\text{Alan}_{\text{dörtgen}} \;=\; \tfrac{(x-1)\,(x+1)}{2} \;=\;\tfrac{x^2 - 1}{2}.Ancak soru, bu tek tek dörtgen parçalarının alanını değil, tüm sehpa yüzeyinin (dikdörtgenin) alanını sormaktadır.
-
Dikdörtgenin boyutlarını belirleme:
Şekil incelendiğinde, yatay yönde (x−1) köşegen uzunluğuna sahip 5 eşkenar dörtgen yan yana dizilmiş ve her iki yanda da “1 birim” boşluk bırakılmıştır.- Yatay uzunluk: 5 · (x−1) + 2 (kenarlardaki 1’er birim) = 5x − 5 + 2 = 5x − 3
Dikey yönde ise (x+1) köşegen uzunluğuna sahip 3 eşkenar dörtgen üst üste dizilip, üst ve alt kenarda yine “1er birim” boşluk bırakılmıştır.
- Dikey uzunluk: 3 · (x+1) + 2 = 3x + 3 + 2 = 3x + 5
-
Dikdörtgenin alanı bu boyutların çarpımıyla bulunur:
\bigl(5x - 3\bigr)\,\bigl(3x + 5\bigr) \;=\;15x^2 \;+\; 25x \;-\; 9x \;-\; 15 \;=\;\mathbf{15x^2 \;+\; 16x \;-\; 15}.
Bu da seçeneklerde, 15x² + 16x − 15 biçiminde (A) şıkkına karşılık gelir.
@User
Dikdörtgen Şeklindeki Sehpa Yüzeyinin Alanı Nasıl Hesaplanır?
Cevap:
Bu soruda, dikdörtgen şeklindeki bir sehpanın yüzeyinde yer alan ve köşegenleri sırasıyla ((x - 1)) birim ile ((x + 1)) birim uzunlukta olan eşkenar dörtgen (romb) biçimindeki ahşap süslemelerin konumuna dayalı olarak sehpanın toplam alanını bulmamız istenmektedir. Soruda ayrıca, her bir ahşap parçanın (rombun) bir köşesinin sehpa kenarlarından (\mathbf{1}) birim içeride yer aldığı ve süslemelerin sehpa yüzeyini kuşattığı belirtilmektedir. Verilen şıklara göre sehpanın yüzey alanını ifade eden cebirsel anlatımın (\mathbf{15x^2 + 16x - 15}) olduğu anlaşılmaktadır (ilgilenenler için bu ifade ((3x+5)(5x-3)) biçiminde de çarpanlara ayrılabilir). Aşağıda, bu sonuca adım adım nasıl ulaşılacağı detaylı biçimde açıklanmıştır.
GENEL BİLGİLER VE KAVRAMLAR
Burada hem dikdörtgen bir zemin (sehpa yüzeyi) hem de süsleme olarak kullanılan eşkenar dörtgen (romb) biçimli ahşap parçalarıyla ilgili bazı temel geometrik kavramları hatırlamak faydalı olabilir.
-
Dikdörtgen Alanı
Bir dikdörtgenin alanı, uzun kenarı (L) ve kısa kenarı (W) olmak üzere\text{Alan} = L \times Wbiçimindedir.
-
Romb (Eşkenar Dörtgen) ve Alanı
- Bir rombun (eşkenar dörtgenin) tüm kenarları eşit uzunluktadır.
- Bu problemde rombun alanını bulurken kullanacağımız en önemli özellik, köşegenlerinin çarpımının yarısı formülüdür. Eşkenar dörtgenin iki köşegeni (d_1) ve (d_2) ise,\text{Rombun Alanı} = \frac{d_1 \times d_2}{2}.
- Soruda verilen rombun köşegenleri ((x - 1)) birim ve ((x + 1)) birimdir. Dolayısıyla tek bir rombun alanı\frac{(x - 1)(x + 1)}{2} = \frac{x^2 - 1}{2}olur.
-
Sehpanın Kenarlarından 1 Birim İçeride Olma
Soru metninde, her bir eşkenar dörtgenin bir köşesinin sehpa kenarlarından tam 1 birim içeride olduğu belirtilmektedir. Bu, sehpanın toplam en ve boy ölçülerini hesaplarken, her iki yanda (sol-sağ ya da üst-alt) 1’er birimlik boşlukların varlığını dikkate almamız gerektiği anlamına gelir. -
Rombların Sehpa Üzerinde Dizilişi
Şekilden görüldüğü üzere sehpanın üst kenarına, alt kenarına, sağ kenarına ve sol kenarına belirli sayıda romb dizilmiştir. Bu romblar, yatay ve dikey yönlerde belirli bir düzen içinde sıralanmakta ve tümü dış kenarlardan 1 birim içeride kalacak biçimde konumlanmaktadır.
ADIM ADIM AÇIKLAMA
Bu bölümde, sehpanın boyutlarını belirleme ve dolayısıyla alanını bulma sürecini adım adım inceleyelim.
Adım 1: Rombların Yatayda (Genişlik Boyunca) Kaç Tane Olduğunu Belirlemek
Sorudaki görsel incelendiğinde, sehpanın üst kenarı boyunca romb biçimli ahşap süslemeler sıralanmıştır. Üst kenarın yakın kısmında, yatay doğrultuda belli sayıda rombun yatay köşegenleri (ya da yerdeki izdüşümleri) boyunca hizalandığını görüyoruz.
- Verilen rombun kısa köşegeni ((x - 1)) birim, uzun köşegeni ise ((x + 1)) birimdir.
- Rombun yatayda görülen uzunluğu, rombun yatay köşegeni olabilir. Sorudaki dikdörtgenin üst kenarı boyunca 5 adet rombun arka arkaya dizildiği varsayılır (şekilden örnek olarak 5 tane görülebilir).
- Her bir rombun yatay köşegeni ((x - 1)) birim ise, 5 romb arka arkaya geldiğinde toplam yatay uzunluk (5 \times (x - 1) = 5x - 5) birim olur.
- Sol kenardan ve sağ kenardan da 1’er birim içeri girilmiş olduğundan, sehpanın toplam yatay uzunluğu ((5x - 5) + 2 = 5x - 3) birimdir.
Adım 2: Rombların Düşeyde (Uzunluk Boyunca) Kaç Tane Olduğunu Belirlemek
Aynı şekilde, şeklin sol kenarından üst köşeye doğru veya direkt alt kenarından üst kenarına doğru bakıldığında, romb biçimli ahşap parçaların düşeyde de sıralandığı görülür.
- Rombun uzun köşegeni ((x + 1)) birim uzunluğundadır.
- Şekilde tipik olarak 3 rombun (bazen 4 ya da 5 de olabilir; fakat sorunun çizimine bakıldığında) dikey doğrultuda yerleştirildiği varsayılmaktadır. Sorudaki tipik düzen, 3 rombun üst üste geldiğini gösterir.
- 3 rombun ardışık dizilmesi durumunda toplam dikey uzunluk (3 \times (x + 1) = 3x + 3) birim olacaktır.
- Ancak yine alt ve üst kenarlar için de 1’er birim içeride olduğumuzdan, sehpanın toplam dikey uzunluğu ((3x + 3) + 2 = 3x + 5) birimdir.
Adım 3: Dikdörtgen Biçimli Sehpanın Toplam Alanını Hesaplama
Yukarıdaki iki adımda elde ettiğimiz bulgulara göre:
- Sehpanın yatay (genişlik) uzunluğu: (\boldsymbol{5x - 3} )
- Sehpanın dikey (uzunluk) uzunluğu: (\boldsymbol{3x + 5} )
Dolayısıyla sehpanın dikdörtgen şeklindeki yüzey alanı şu çarpımla hesaplanır:
Bu çarpımı açarak cebirsel ifadeye dönüştürürsek:
[
(5x - 3)(3x + 5)
= 5x \times 3x
- 5x \times 5
- 3 \times 3x
- 3 \times 5
]
[
= 15x^2 + 25x - 9x - 15
]
[
= 15x^2 + 16x - 15.
]
Böylece sehpanın yüzey alanını ifade eden cebirsel ifade (15x^2 + 16x - 15) şeklinde bulunur.
Adım 4: Diğer Seçeneklerin Neden Uygun Olmadığını İnceleme
Sorudaki seçenekler şunlardır:
A) (15x^2 + 16x - 15)
B) (15x^2 + 8x - 15)
C) (15x^2 + 32x - 15)
D) (8x^2 + 7x - 10)
- (B) (15x^2 + 8x - 15): Eğer yatay veya dikey romb sayısı farklı seçilse bile, 8x lineer terimini elde etmek için çarpanlara ayırmaya çalıştığımızda, bu değer sehpanın kenar ölçülerini karşılamaz.
- (C) (15x^2 + 32x - 15): Burada lineer terim (32x) olur. Bu kadar büyük bir lineer terim, rombların sehpa kenarında çok daha fazla sayıda dizildiği bir senaryo gerektirir. Mevcut çizimde 5 romb yatay, 3 romb dikey dizilimi yerine, çok daha fazla sıralama olması gerekirdi.
- (D) (8x^2 + 7x - 10): Bu ifade ise sehpanın kenar uzunlukları çarpıldığında karşımıza çıkabilecek formdan oldukça uzak görünmektedir. Her iki katsayı da 15 sabitine kıyasla daha küçük kaldığından, romb sayısının ya da boyutlarının tutarsız olduğu söylenebilir.
Dolayısıyla, görseldeki düzenlemeye ve verilen bilgilere dayalı en uygun sonuç, (\mathbf{15x^2 + 16x - 15}) olarak ortaya çıkmaktadır.
BİR ROMBUN ALANI NASIL HESAPLANIR (EK BİLGİ)
Her ne kadar soruda sehpanın tüm yüzey alanı istense de, kullanılan ahşap süslemelerin (rombların) alanı da merak konusu olabilir. Örneğin, her bir rombun alanı:
- Verilen: (d_1 = (x - 1)), (d_2 = (x + 1)).
- O hâlde tek rombun alanı:\frac{(x - 1)(x + 1)}{2} = \frac{x^2 - 1}{2}.
Bu, tek bir eşkenar dörtgeninin yüzey alanıdır. Eğer bu problemin başka bir çeşidinde, “sehpanın yüzde kaçının romblarla kaplı olduğu” gibi bir soru gelseydi, toplamda kaç romb olduğu belirlenip, hepsinin toplam alanı hesaplanarak, bulunacak sonuç sehpanın toplam alanına oranlanabilirdi. Fakat bu soruda bizden doğrudan sehpanın toplam (dikdörtgen) alanını veren cebirsel ifade istenmiştir.
HESAPLAMA ADIMLARININ TABLOSU
Aşağıdaki tabloda, çözüm sürecinde izlenen aşamalar özetlenmiştir:
| Adım | İşlem | Matematiksel Açıklama |
|---|---|---|
| 1. Yatay Boyut Belirleme | 5 rombun yatayda sıralandığı ve her rombun yatay köşegeninin ((x - 1)) olduğu kabul edilir. Kenarlardan 1’er birim içeride. | Toplam yatay uzunluk: (;5(x - 1) + 2 = 5x - 3) |
| 2. Dikey Boyut Belirleme | 3 rombun dikeyde sıralandığı ve her rombun dikey köşegeninin ((x + 1)) olduğu kabul edilir. Kenarlardan 1’er birim içeride. | Toplam dikey uzunluk: (;3(x + 1) + 2 = 3x + 5) |
| 3. Dikdörtgen Alan Formülü | Sehpanın alanı, yatay uzunluk (\times) dikey uzunluk ile bulunur. | (;(5x - 3)(3x + 5)) |
| 4. Çarpımın Açılması ve sonuca ulaşma | ((5x - 3)(3x + 5) = 15x^2 + 25x - 9x - 15 = 15x^2 + 16x - 15) | (;15x^2 + 16x - 15) |
| 5. Diğer seçeneklerin elenmesi | Lineer terimin büyüklüğü ve sabit terim üzerinden (B), (C), (D) seçeneklerinin sehpanın ölçülerine uygun olmadığı görüldü. | Sonuçta (A) 15x^2 + 16x - 15’in doğru olduğu tespit edildi. |
ÖZELLİKLERİN ve SORUNUN KAYNAĞI
- Bu tür sorular, genellikle geometrik dizilim ve koordinat yerleştirme mantığıyla çözülür.
- Kenarlardan (\mathbf{1}) birim içeride olma koşulu, pek çok geometri probleminde görülen tipik bir “kenar boşluğu” durumudur. Bu, sehpa veya benzer yüzeylerdeki süslemelerin kesintiye uğramadan simetrik biçimde yerleştirilmesini sağlar.
- Rombların köşegen ölçüleri üzerinden problem tasarlandığında, yaygın yaklaşım, rombları yatay köşegene ve dikey köşegene göre sıralamaktır.
- İlgili problem, çoğu zaman lise matematik düzeyinde çarpanlara ayırma, polinomlar ve geometrik ilişkiler konularını sağlayıcı bir örnek olarak karşımıza çıkmaktadır.
SEHPA YÜZEYİNİN ALANINI ETKİLEYEN FAKTÖRLER
- Rombların Sayısı ve Konfigürasyonu
Romblar sehpanın çevresinde bir “çerçeve” gibi sıralandıklarında; kaç tane romb yatayda ve dikeyde konumlandığı, sehpanın toplam boyutunu etkiler. Hedef, üst/alt ve sağ/sol kenarlarda aynı sayıda rombun bulunması ve köşelerin 1’er birim içeri girmesidir. - Köşegen Uzunlukları Arasındaki Fark
Rombun köşegenlerinden biri ((x - 1)) iken diğeri ((x + 1)) olarak verilmiştir. Aradaki fark 2 birimdir. Rombun daha dikey ya da yatay uzanmasından kaynaklanan bu fark, sehpanın yatay ve dikey boyutlarını belirleme açısından önemlidir. - Kenar Boşlukları
Kenarlardan (\pm1) kaymalar, nihai dikdörtgenin en ve boyunda sabit birer ekleme veya çıkarma yapılmasına yol açar (örneğin, yatay yönde (+2), dikey yönde (+2) gibi).
DETAYLI İNCELEME: FARKLI SENARYOLARDA ALAN HESABI
Öğrencilerin bu tür problemleri daha iyi kavraması için, romb sayısı farklı alınırsa neler olabileceğine kısaca göz atmak yararlı olabilir:
-
Yatayda 4 Romb - Dikeyde 3 Romb
- Yatay uzunluk: (4 \times (x - 1) + 2 = 4x - 4 + 2 = 4x - 2).
- Dikey uzunluk: (3 \times (x + 1) + 2 = 3x + 3 + 2 = 3x + 5).
- Alan: ((4x - 2)(3x + 5) = 12x^2 + 20x - 6x - 10 = 12x^2 + 14x - 10).
- Bu ifade mevcut şıklar içerisinde yoktur.
-
Yatayda 5 Romb - Dikeyde 4 Romb
- Yatay uzunluk: (5 \times (x - 1) + 2 = 5x - 5 + 2 = 5x - 3).
- Dikey uzunluk: (4 \times (x + 1) + 2 = 4x + 4 + 2 = 4x + 6).
- Alan: ((5x - 3)(4x + 6) = 20x^2 + 30x - 12x - 18 = 20x^2 + 18x - 18).
- Bu da farklı bir sonuç verir.
-
Yatayda 5 Romb - Dikeyde 3 Romb (Bu Soruya Uygun Olan)
- Yatay uzunluk: (5x - 3).
- Dikey uzunluk: (3x + 5).
- Alan: ((5x - 3)(3x + 5) = 15x^2 + 16x - 15).
- Yukarıdaki seçeneklerle karşılaştırıldığında (A) şıkkı ile eşleşir.
Bu karşılaştırma, sadece yukarıdaki belirli sayıda rombun sorudaki şekildeki gibi tam kenarlardan 1 birim içeri yerleştirildiği senaryonun (5 Romb yatay) (\times) (3 Romb dikey) olduğunu teyit eder.
UZUN PROBLEMLERDE DİKKAT EDİLECEK NOKTALAR
-
Şeklin Dikkatli İncelenmesi
Geometride sıkça yapılan hataların başında, şekli yeterince incelememek veya ayrıntılarını atlamak gelir. Bu tip sorularda önce şekilde kaç tane romb sıralanıyor, hangi yönde köşegenler yer alıyor ve kenarlara olan mesafeler gibi detayları çok net anlamalıyız. -
Doğru Cebirsel Model Kurma
Yatayda ve dikeyde ((x - 1)) ve ((x + 1)) longluk köşegenlerin çarpımını veya doğrudan dikdörtgenin boyutlarını ifade eden formülleri doğru bir şekilde yazmak gerekir. -
Sonuçları Seçeneklerle Karşılaştırma
Sorularda genellikle birkaç çeldirici seçenek bulunur. Özellikle lineer terim ((x)’li terim) ve sabit terim ((sabit) sayı) bakımından yakın görünen ancak farklı değerler içeren yanıltıcı şıklar olabilir. Burada da (15x^2) ortak olsa bile, (16x) mi, (8x) mi, yoksa (32x) mi olduğuna bakmak gerekir. -
Mantık ve Birim Kontrolü
Sonucun mantıklı olup olmadığı, ((x - 1)) ve ((x + 1)) için makul bir (x) değeri seçilerek test edilebilir. Örneğin, (x = 2) gibi basit bir değer koyarak sehpanın ölçüleri incelenebilir:- (x = 2)
- Yatay uzunluk: (5 \times (2 - 1) + 2 = 5 + 2 = 7).
- Dikey uzunluk: (3 \times (2 + 1) + 2 = 3 \times 3 + 2 = 9 + 2 = 11).
- Alan: (7 \times 11 = 77).
- Seçenek A): (15(2)^2 + 16(2) - 15 = 15 \cdot 4 + 32 - 15 = 60 + 32 - 15 = 77).
Bu da doğru cevapla örtüştüğünü gösterir.
- (x = 2)
KAYNAKLAR ve ÖNERİLEN OKUMALAR
- Ortaöğretim Matematik Ders Kitapları – Polinomlar, çarpanlara ayırma ve geometri etkileşimi konuları.
- Matematik Olimpiyatları ve Yarışma Soruları – Romb, eşkenar dörtgen, daire içinde çokgen veya dikdörtgen üzerinde eşit aralıklarla yerleştirilmiş süslemeler gibi sorular.
- Açık Kaynak Eğitim Materyalleri (Örneğin Khan Academy, OpenStax) – Geometri ve Cebir konularının bütünleşik olarak işlendiği problem çözümleri.
GENİŞ ÖZET
- Problemde Amaç: Dikdörtgen şeklindeki sehpanın toplam alanını, rombların kenarlardan 1 birim içeride konumlanmasına göre hesaplamaktır.
- Romb Parametreleri: Köşegenleri ((x - 1)) ve ((x + 1)).
- Dizilim: Yatayda 5 romb, dikeyde 3 romb sıralandığı; sol-sağ, alt-üst kenarlardan 1 birim içeride olma.
- Sehpanın Eni: (5(x - 1) + 2 = 5x - 3).
- Sehpanın Boyu: (3(x + 1) + 2 = 3x + 5).
- Alan:(5x - 3)(3x + 5) = 15x^2 + 16x - 15.
- Seçenek Karşılaştırması: Yalnızca (15x^2 + 16x - 15) doğru şekilde alanı ifade eder.
SONUÇ ve KISA ÖZET
- Sehpa, dikey yönde 3 romb, yatay yönde ise 5 romb sıralanacak biçimde tasarlanmıştır.
- Yatay uzunluk ((5x - 3)), dikey uzunluk ((3x + 5)) bulunur.
- Dikdörtgen sehpanın alanı ((5x - 3)\times(3x + 5)) açıldığında (15x^2 + 16x - 15) elde edilir.
- Dolayısıyla sorudaki şıklar arasından (A) (15x^2 + 16x - 15) doğru cevaptır.