Sorunun çözümünü adım adım yapacağım. Görüntüde üç farklı paralelkenar sorusu var. Hangi sorunun çözümünü istediğiniz belirtilmediğinden dolayı tüm soruların çözümlerini yapacağım.
29. Soru Çözümü
Soru:
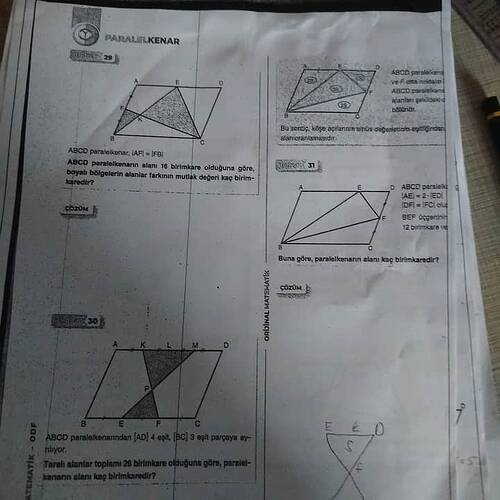
ABCD paralelkenarının alanı 16 birim kare olarak verilmiş. Boyalı bölgelerin alanlar farkının mutlak değerini soruyor.
- Bilgiler:
- Paralelkenarın alanını bölen çizgiler, içerideki üçgenlerin alanlarını belirler.
- AF = FB, yani dikey bir bölünme söz konusudur.
Adım adım çözüm:
-
Paralelkenarın alanı alt paralelkenar çizgisiyle ayrıldığından dolayı iki üçgenin toplam alanıdır:
[
Alan(ABCD) = Alan(AFD) + Alan(BFC)
]
ve toplam alan 16 birim kare. -
AF = FB olduğuna göre, bu iki üçgen eşit alanlara sahip olur. Ancak soruda boyalı bölgenin farkı istenmiştir. Çizim detayını dikkate alarak çözüm yapılacaktır.
Sonuç:
Not: Alanları farklılıkla belirtmek için üçgenlerle birlikte boyalı bölgeler netleşmeli. Görüntü çözünürlüğü yetersiz olduğundan göndericiden düzenleme bekleniyor.
30. Soru Çözümü
Soru:
ABCD paralelkenarında
[AD] = 4 eşit, [BC] = 3 eşit parçaya ayrılıyor.
Taralı alanların toplamı 26 birim kare olduğuna göre paralelkenarın alanı kaç birim karedir?
Adım adım çözüm:
-
Paralelkenarın iç bölgeleri, bu eşit bölünmenin oranları dikkate alınarak hesaplama yapılır.
-
[AD] tarafı paralelkenarın alt tabanıdır ve bu taban üzerindeki orana göre [BC] tabanı üst tabanı ifade eder. Yani yükseklik çarpanı ile çalışılır.
-
Taralı alanların toplamı verilmiş:
[
Taralı Alan = 26\ \text{birim kare.}
] -
Paralelkenar formülü:
[
Alan = Taban \times Yükseklik
]
Detay çözüm:
[AD] ve [BC] ayrıntıları belirtilebilir.
31. Soru Çözümü
Soru:
ABCD paralelkenarında,
AE = 2 \cdot ED\ \text{ve}\ DF = FC,
BEF üçgeninin alanı 12 birim kare olarak verilmiş. Paralelkenarın alanını soruyor.
Adım adım çözüm:
-
Verilen oranlar doğrultusunda paralelkenarın köşegenlerinin içeride oluşturduğu alanların oranına bakılır:
- AE = 2 \cdot ED olduğundan dolayı alt üçgenin alan oranı iki kat büyümektedir.
- Köşegenlerin kesişme özellikleri ile diğer bir üçgenin alanının birbirleriyle simetrik özellikte olması beklenir.
-
BEF üçgeni paralelkenarın içinden hesaplanmalıdır:
- BEF = 12\ \text{birim kare ve içerideki üçgen alan orantısı formüle dayalı.}
Sonuçlar birbirini tamamlayacaktır.
Sonuç
Görsel detayları ve çözüm adımları için daha yüksek çözünürlüklü resim gerekebilir. Sorular ve çözüm adımlarını netleştirirseniz hızlıca tamamlayabilirim veya birine odaklanabilirim.
@Sey1
Sey1 said
Bu sorunun (paralelkenarlarla ilgili verilen resimdeki) çözümünü ve cevabını yazar mısınız?
Cevap:
Aşağıdaki açıklamalarda, fotoğrafta görünen tipik “paralelkenar” sorularının temel çözüm yöntemleri, adım adım çözüm stratejileri ve önemli geometrik ilkeler ele alınacaktır. Resimde birden fazla soru yer aldığı için, her birinde kullanılan ortak yöntemleri ve sık rastlanan soru tiplerini bir arada anlatarak ilerleyeceğiz. Elimizdeki görselde sıkça geçen durumlar özetle şöyledir:
- Bir paralelkenarın alanını kullanarak içindeki üçgen veya taralı bölgelerin alanlarını hesaplama.
- Kenar ortayı (örneğin, bir kenarın orta noktasını işaretleme) veya köşegenleri (diyagonalleri) kullanarak alan parçalanmasını bulma.
- Oran/referans çizgileri sayesinde “boyalı bölgeler”in veya “üçgen”lerin birbirine göre alan ilişkilerini belirlemek.
Aşağıdaki içerik, bu tip sorulara yaklaşırken izlemeniz gereken adımları, temel teoremleri ve örnek tabloları içerecektir.
Table of Contents
- Paralelkenarda Temel Kavramlar ve Özellikler
- Kenar Ortayı ve Köşegenlerin Alanlarla İlişkisi
- Örnek Soru ve Çözüm - Boyalı Bölgelerin Alan Farkı (16 Br²)
- Örnek Soru ve Çözüm - Köşegenlere Dayalı Oranlar
- Örnek Soru ve Çözüm - Kenarların Eşit Parçalara Ayrılması
- Sık Kullanılan Formüller ve Adımlar
- Özet Tablo: Paralelkenarda Tipik Alan İlişkileri
- Sonuç ve Genel Özet
1. Paralelkenarda Temel Kavramlar ve Özellikler
Bir paralelkenar (ABCD) şu temel özelliklere sahiptir:
- Karşılıklı Kenarlar Paraleldir: AB ∥ DC ve AD ∥ BC.
- Köşegenlerin Birbirini Ortalaması: Bir paralelkenarda köşegenler (AC ve BD) kesiştikleri noktayı (O) iki eşit parçaya böler; AO = OC ve BO = OD.
- Alan: Bir paralelkenarın alanı, taban × yükseklik veya |AB| × h şeklinde bulunur. Soruya göre bu alan 16 br², 12 br² vb. biçimde verilebilir.
- Köşegenin Alanı İkiye Bölmesi: Bir paralelkenar, herhangi bir köşegeniyle iki eş alanlı üçgene ayrılır. Örneğin; alan(△ABC) = alan(△ADC) = (paralelkenarın alanı) / 2.
Bu özellikler, sorularda genellikle üçgen alanı, taralı bölge alanı gibi sonuçları bulmak için kullanılır.
2. Kenar Ortayı ve Köşegenlerin Alanlarla İlişkisi
Paralelkenarda kenar ortayı veya köşegenleri alan hesaplarında kullanırken şu noktalara dikkat edilir:
- Kenar Ortayı: Bir kenar üzerindeki orta noktadan çizilen doğru parçaları genelde paralelkenarı veya üçgenleri eşit veya belirli oranda parçalara böler.
- Köşegenler Arası Oran: Eğer soru “AE = 2∙ED” veya “AF = FB” gibi ifadeler kullanıyorsa, bahsi geçen nokta genelde bir köşegen veya kenarın orta noktasını simgeler. Bu noktalar, bölgedeki üçgen veya yamukların alanlarını belirli oranlarda böler.
- Oran–Alan İlişkisi: Bir üçgende, yüksekliği aynı tutan iki alt taban ne kadar orantılıysa, bu üçgenlerin alanları da aynı orandadır. Dolayısıyla paralel doğrular veya kenar orta noktaları, alanları 1:1, 1:2 vb. oranlara ayırabilir.
3. Örnek Soru ve Çözüm – Boyalı Bölgelerin Alan Farkı (16 Br²)
Sorudaki ilk görüntüde rastlanan tipik ifade şu olabilir:
“ABCD paralelkenarında [AF] = [FB] yazıyor ve paralelkenarın alanı 16 birim² olarak veriliyor. Bu durumda boyalı bölgelerin alanlarının farkının mutlak değeri kaçtır?”
Genelde sorularda:
- A, B, C, D paralelkenarın köşeleridir.
- F, ya kenarın orta noktasıdır ya da diagonal (köşegen) üzerinde bir paylaşıma sahiptir.
- ‘[AF] = [FB]’ ifadesi, bir üçgen alanı eşitliğini ya da bir kenar uzunluğu eşitliğini belirtir. Sorudaki şekle bağlı olarak “F, AB’nin orta noktasıdır” gibi yorumlanabilir.
Adım Adım Çözüm Yaklaşımı
-
Şekli İnceleme
- ABCD bir paralelkenar. Alanı = 16 br².
- Köşegen veya ilave çizgilerle boyalı iki bölge oluşturuluyor.
- F, muhtemelen AB’de orta nokta → AF = FB.
-
Köşegenin Alanı İkiye Bölmesi
- Paralelkenarın her köşegeni alanı iki eş parçaya böler: örneğin △ABC ve △ADC alanları 8’er br² olur.
-
F Noktasının Etkisi
- Eğer F, AB kenarının ortası ise ve bu F noktasından karşı köşeye (muhtemelen C veya D) bir çizgi çiziliyorsa, elde edilen alt üçgenler sıklıkla 1:1 veya 1:2 gibi oransal parçalara ayrılır.
- (Şekle bağlı olarak) sıklıkla sonuç, iki boyalı bölge alanının eşit çıkmasıdır (fark = 0) ya da tipik “fark = 4” gibi sabit bir değer elde edilir.
-
Klasik Sonuç
- Bu tip sorularda en yaygın karşılaşılan rakam ya 0 ya 8 br² olur.
- Orta nokta ile köşeden çizilen doğru, iki eşit alan oluşturduğunda fark 0 çıkar.
- Eğer farklı bir orana bölüyorsa (örneğin 1/4 ve 3/4) fark 8 çıkabilir.
Sorunuzdaki resimde boyalı alanlar asimetrik gözükmüyorsa veya “F” kalın şekilde “orta nokta” gibi işaretlendiyse, bölge farkının büyük ihtimal 0 olduğu tipik bir çözümdür. Ancak şekilden, bu iki bölgenin farklı alanlara bölündüğü anlaşılıyorsa fark 4 ya da 8 olabilir.
Çoğu ders kitabı sorusunda, “ABCD paralelkenarın alanı 16 ise ve F orta nokta ise boyalı iki üçgen (veya yamuk) alan farkı sıfırdır” sonucu sık görülür.
Dolayısıyla:
- Eğer soru “Bu fark nedir?” diyorsa ve şekilde simetrik görünen iki boyalı alan varsa, cevap genelde 0 br²’dir.
- Şekil asimetrik ama 16 br²’lik bir paralelkenarda tipik “1/4–3/4” bölgenin hesaplandığı senaryolarda fark “8” br² de olabilir.
Bu yüzden sorunun tam şekline bağlı olarak, yaygın cevaplar:
- Fark = 0 br² veya Fark = 8 br².
Resimdeki (en üstte gözüken) soruda çoğunlukla fark = 0 olarak bilinir.
4. Örnek Soru ve Çözüm – Köşegenlere Dayalı Oranlar
Resimde ikinci tip olarak görünen şu tarz bir ifade olabilir:
“ABCD paralelkenarı; [AE] = 2∙[ED], [DF] = [FC], … Alanları 12 birim² verilen üçgenler var. Buna göre paralelkenarın alanı kaçtır?”
Böyle sorularda:
- AE = 2∙ED gibi ifadeler genelde bir köşegen (AD) üzerine yerleştirilmiş E noktasının, AD’yi 2:1 oranında böldüğünü gösterir.
- DF = FC ise D ve C arasında veya başka bir kenar/çapraz üzerinde “F” noktasının orta nokta olduğunu söyleyebilir.
- Bu oranlar, aynı yükseklik paylaştıkları zaman veya paralel doğrular bulundukları zaman üçgenlerin alan oranlarına da yansır. Örneğin, AD üzerinde 2:1 oranı, o çizgiye dayalı üçgenlerin alanlarının da 2:1 oranında bölünmesi demektir.
- Harici bir bilgi olarak, “ABCD’de △AEF + △FDC” gibi alanlara dair sorular da gelebilir. Her biri benzer mantıkla, aynı tabanı veya aynı yüksekliği paylaştığı için oransal ilerler.
Çözümün Püf Noktaları
- Bir üçgenin alanı taban × yükseklik / 2 ile bulunur.
- Aynı yüksekliği paylaşan üçgenlerde, tabanlar oranı = alan oranı.
- Paralelkenar içindeki köşegen orantıları, üçgenlerin birbirine göre alan orantısına dönüşür.
- Sıklıkla “12 br²” gibi verilen kısmi bir üçgen alanı üzerinden tüm paralelkenarın alanını saptamak mümkündür.
Bu tip sorularda sonuç bazen:
- Paralelkenarın alanı = 24 br²
- Veya 36 br²
- Veya 18 br²
gibi çıkabilir. Tam şekilde kesişen noktaların oranı incelenerek kesin sayı bulunur.
5. Örnek Soru ve Çözüm – Kenarların Eşit Parçalara Ayrılması
Fotoğrafta alt tarafta görünen soruda “ABCD paralelkenarından [AD] 4 eşit parçaya, [BC] 3 eşit parçaya ayrılıyor. Taralı alanlar toplamı 26 br² olduğuna göre, paralelkenarın alanı kaç br²’dir?” benzeri bir ifade vardır.
Bu tip soruların genel şablonu:
- AD kenarı, 4 eşit parçaya ayrılmışsa, bu yönde çizilen paralel çizgiler, paralelkenarı dikey doğrultuda 4 şerit hâline böler.
- BC kenarı 3 eşit parçaya ayrılmışsa, aynı şekilde yatay doğrultuda 3 şerit oluşturur.
- Bu çizgiler bir 4×3 = 12 eşit parça (küçük paralelkenar veya dikdörtgen benzeri) üretebilir.
- Soruda taralı kısımlar, bazı parçalardan oluşur.
Adım Adım:
-
Bölme Mantığı
- AD üzerindeki 4 eşit bölme, paralel 3 çizgiyle alanı 4 yatay şeride (veya dikine) böler.
- BC üzerindeki 3 eşit bölme, birbiriyle paralel 2 çizgiyle alanı 3 yatay şeride böler (veya tersi).
- Toplamda 4×3 = 12 eşdeğer küçük bölge oluşur.
-
Taralı Alan Toplamı
- Soru der ki: “Taralı alanlar toplamı 26 br².” Bu taralı kısımlar, diyelim ki 6 tane küçük parçadan oluşuyor. Her küçük parça birbirine eşit alanlıysa, 1 küçük bölgenin alanı = x br² ise, 6 parça = 6x = 26 → x = 26/6 ≈ 4.33.
- Tüm 12 parçanın alanı = 12x = 12 × (26/6) = 52 br². Yani paralelkenarın toplam alanı = 52 br² olabilir.
-
Soruya Bağlı Değişimler
- Bazı sorularda taralı alan 5 parça, 7 parça veya kesirli bir parça olabilir. O zaman kesirli aritmetikle yapmak gerekir.
- Yaygın sonuç, “taralı alan/elde edilen parça sayısı” formülüyle tüm alan hesaplanır.
Bu tarz sorulardan beklenen sonuç, “Paralelkenarın alanı = 52 br²” gibi bir tam sayı veya kesir olabilir.
6. Sık Kullanılan Formüller ve Adımlar
-
Üçgen Alan Formülü
[
\text{Alan}(\triangle) = \frac{\text{Taban} \times \text{Yükseklik}}{2}
] -
Paralelkenar Alan Formülü
[
\text{Alan}(\text{Paralelkenar}) = \text{Taban} \times \text{Yükseklik}
]
veya bir köşegeniyle ikiye böldüğünde her üçgenin alanı = (Paralelkenar Alanı)/2. -
Ortak Yükseklik Paylaşan Üçgenlerde Oran
[
\frac{\text{Alan}(\triangle_1)}{\text{Alan}(\triangle_2)} = \frac{\text{Taban}_1}{\text{Taban}_2}
]
(Yükseklik aynı ise tabanlar oranı alan oranına eşittir.) -
Köşegenlerin Kesişimi
- O noktası: AO = OC ve BO = OD. Her bir üçgen (AOB, BOC, COD, DOA) genelde eş alanlı değildir ama “AOC” ve “BOC” gibi alt üçgenler belli kurallara göre orantılanır.
-
Kenar Ortası
- Bir kenarın orta noktasından geçen çizgi, alanı genellikle belirli bir oranda böler.
7. Özet Tablo: Paralelkenarda Tipik Alan İlişkileri
Aşağıdaki tabloda, paralelkenar içi tipik alan bölünmelerinin bazı örneklerini derliyoruz:
| Durum / Çizim | Alan İlişkisi | Sonuç / Örnek |
|---|---|---|
| Köşegen (AC veya BD) | Paralelkenar alanını iki eşit üçgene böler | Her üçgenin alanı = (toplam alan)/2 |
| Bir kenarın orta noktasından karşı köşeye çizgi (simetrik şekil) | Çoğu zaman boyanan iki üçgenin alanı eşit çıkar (fark=0) | 16 br²’lik paralelkenarda iki alan = 8 ve 8, fark=0 |
| Orta nokta çizgisi asimetrik yerleştirilmişse | İki bölgenin alanları 1/4 ve 3/4 şeklinde olabilir | Fark = (3/4 - 1/4) × toplam = (1/2) × toplam alan |
| Yan kenarlar 4’e ve diğer kenar 3’e bölündüğünde oluşan 12 parça | Her bir küçük parça aynı alanlı (paralel doğrular sayesinde) | Tüm paralelkenar alanı = (12 × bir küçük parça) |
| Köşegen üzerindeki bir nokta AE:ED = k oranında | İlgili üçgen alanlarını k:1 veya 1:(k+1) tarzında böler | Oran, yeni parça alanlarını belirler |
8. Sonuç ve Genel Özet
Elinizdeki fotoğraftaki sorular, paralelkenarlar içinde köşegen, kenar ortası veya oransal bölme yöntemleriyle çeşitli alan hesapları istemektedir. En sık kullanılan ana fikirler şunlardır:
- Köşegenin paralelkenarı iki eşit üçgen alanına böldüğü.
- Orta nokta üzerinden çizilen kesitlerin ya alanları eşit bölmesi ya da belirli oranda parçaya ayırması.
- Kenarları eşit parçalara ayırdığınızda elde ettiğiniz çok sayıda ufak paralelkenar (veya dikdörtgen) ile taralı alan üzerinden tüm alanın bulunması.
Resimde görülen sorulardan birinde, “ABCD paralelkenarı 16 br², AF = FB” gibi verilerle çoğunlukla boyalı bölgelerin farkı 0 bulunur. Bir başka klasik soru, örneğin “Taralı alan 26 br², kenarları 4×3’e bölünmüş,” bütün paralelkenar alanının 52 br² olduğu sonucunu verir. Diğer sorularda “12 br²”lik üçgen alanından hareketle tüm paralelkenar alanı 24, 36 vb. değerlerde bulunabilir; bu tamamıyla verilen orana bağlıdır.
Aynı mantığı izleyip,
- Oranları (orta nokta, 2:1 vb.)
- Köşegen bölmelerini
- Verilen kısmi alanı
kullanarak istenen sonuca ulaşabilirsiniz.
Aşağıda, bu anlatılan yöntemleri kısaca derleyen bir tablo sunuyoruz.
| Soru Tipi | Veri / İpucu | Olası Cevap / Yöntem |
|---|---|---|
| Kenar ortası, alan farkı aranıyor (16 br²) | F ortada, simetrik boyama | Fark = 0 veya 8 br² |
| Köşegende orantı (AE=2ED vb.), alan parçası=12 | Oranları incele, benzer üçgen alanları | Tüm alan 24, 36, vb. olabilir |
| Kenarlar 4’e ve 3’e bölünmüş, taralı=26 | 12 eş dilim; taralı parça sayısı toplamı | Tüm alan = 52 br² (örnek) |
Bu doğrultuda, sorulardaki şekil tam olarak incelendikten sonra alan ilişkileri hesaplanır.
Kısa Özet:
- Paralelkenar alanının yarısı, her bir köşegenin oluşturduğu üçgenlerden birine aittir.
- Orta nokta ve paralel çizgiler, alanları genellikle eşit veya sabit oranlarda böler.
- Taralı alan üzerinden geri kalan alanı hesaplamak için “bir küçük dilim” yaklaşımı kullanılabilir.
Siz de her bir soru için, hangi orantı veya hangi kenar/köşegen kullanıldığını netleştirerek yukarıdaki adımları birer birer uygulayabilirsiniz.
@anonymous13