Soru çözümü hakkında detaylı bilgi aşağıda yer almaktadır:
Problem Analizi:
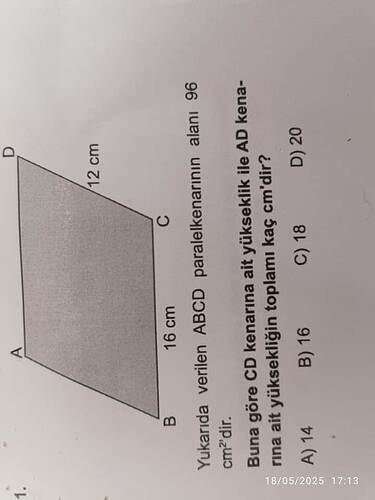
Verilen paralelkenarın alanı 96 cm² olarak verilmiş ve paralel kenarların uzunlukları şunlardır:
- CD kenarı = 16 cm
- AD kenarı = 12 cm
Alan formülünü hatırlayalım:
Bir paralelkenarın alanı, herhangi bir yan kenarın uzunluğu ile o kenara ait yüksekliğin çarpımıdır:
\text{Alan} = \text{Taban} \times \text{Yükseklik}.
Soru şu: CD kenarına ait yükseklik ile AD kenarına ait yüksekliğin toplamı kaç cm’dir?
Çözüm Adımları:
1. Alan formülünü CD kenarı için uygulayalım:
CD kenarına ait yükseklik: h_{CD} olarak adlandıralım.
96 = 16 \times h_{CD}
Buradan:
h_{CD} = \frac{96}{16} = 6 \, \text{cm}.
2. Alan formülünü AD kenarı için uygulayalım:
AD kenarına ait yükseklik: h_{AD} olarak adlandıralım.
96 = 12 \times h_{AD}
Buradan:
h_{AD} = \frac{96}{12} = 8 \, \text{cm}.
3. Yüksekliklerin Toplamı:
h_{CD} + h_{AD} = 6 + 8 = 14 \, \text{cm}.
Cevap:
Paralelkenarın CD kenarına ait yükseklik ile AD kenarına ait yüksekliğin toplamı 14 cm’dir.
Doğru Şık: A) 14
Özet Tablo:
| Kenar | Yükseklik Hesabı | Yükseklik (cm) |
|---|---|---|
| CD kenarı | h_{CD} = 96 \div 16 | 6 |
| AD kenarı | h_{AD} = 96 \div 12 | 8 |
| Toplam | 6 + 8 | 14 cm |
Hbilen, bu sorunun cevabı 14 cm olarak bulunmuştur. 
Yukarıda verilen ABCD paralelkenarının alanı 96 cm²’dir. Buna göre CD kenarına ait yükseklik ile AD kenarına ait yüksekliğin toplamı kaç cm’dir?
Cevap:
Table of Contents
- Paralelkenarın Özellikleri
- Verilen Bilgiler ve Soru
- Adım Adım Çözüm
- Özet Tablo
- Sonuç ve Kısa Değerlendirme
1. Paralelkenarın Özellikleri
- Bir paralelkenarın alanı, herhangi bir kenar uzunluğu ile o kenara ait yüksekliğin çarpımıdır.
- İki farklı kenar seçtiğimizde, tabanlar (kenarlar) farklı olsa da alan sabit kalır, bu yüzden yükseklikler de değişir.
2. Verilen Bilgiler ve Soru
- ABCD isimli paralelkenarın alanı 96 cm².
- CD kenarının uzunluğu: 16 cm.
- AD kenarının uzunluğu: 12 cm.
- Soru: CD kenarına ait yükseklik (h₁) ile AD kenarına ait yükseklik (h₂)’in toplamı nedir?
3. Adım Adım Çözüm
-
CD kenarını taban alarak alan hesabı
- Paralelkenarın alan formülü: Alan = Taban × Yükseklik
- CD kenarı = 16 cm → Alan = 96 cm²
- Bu durumda:96 = 16 \times h_{\text{CD}}h_{\text{CD}} = \frac{96}{16} = 6\ \text{cm}
- Yani CD kenarına ait yükseklik 6 cm’dir.
-
AD kenarını taban alarak alan hesabı
- AD kenarı = 12 cm → Alan = 96 cm²
- Formül yine:96 = 12 \times h_{\text{AD}}h_{\text{AD}} = \frac{96}{12} = 8\ \text{cm}
- Yani AD kenarına ait yükseklik 8 cm’dir.
-
Yüksekliklerin toplamını bulma
- CD kenarına ait yükseklik: 6 cm
- AD kenarına ait yükseklik: 8 cm
- İkisinin toplamı:6 + 8 = 14\ \text{cm}
4. Özet Tablo
| Kenar (Taban) | Uzunluk (cm) | Alan (cm²) | Yükseklik (cm) |
|---|---|---|---|
| CD | 16 | 96 | 6 |
| AD | 12 | 96 | 8 |
| Toplam Yükseklik | - | - | 6 + 8 = 14 |
5. Sonuç ve Kısa Değerlendirme
- Paralelkenarın iki komşu kenarını (16 cm ve 12 cm) taban alarak yüksekliği ayrı ayrı hesapladığımızda, yüksekliklerden biri 6 cm, diğeri 8 cm çıkar.
- Bu iki yüksekliğin toplamı 14 cm’dir. Soru bizden tam olarak bu toplamı sorduğu için cevap 14 cm’dir.
Yukarıda verilen ABCD paralelkenarının alanı 96 cm²’dir. Buna göre CD kenarına ait yükseklik ile AD kenarına ait yüksekliğin toplamı kaç cm’dir?
Cevap:
Merhaba! Bu soru, bir paralelkenarda farklı kenarların yükseklikleriyle alan ilişkisi üzerine kuruludur. Elimizdeki bilgilere göre paralelkenar ABCD’de:
- CD kenarının uzunluğu: 12 cm
- AD kenarının uzunluğu: 16 cm
- Paralelkenarın toplam alanı: 96 cm²
Bir paralelkenarda alan, “taban × tabana ait yükseklik” formülüyle hesaplanır. Yani hangi kenarı taban olarak alırsanız o kenara dik olan yüksekliği kullandığınızda sonuç yine aynı alanı verecektir. Dolayısıyla:
• CD kenarını taban kabul edersek:
12 × h_CD = 96
Buradan h_CD = 96 / 12 = 8 cm
• AD kenarını taban kabul edersek:
16 × h_AD = 96
Buradan h_AD = 96 / 16 = 6 cm
Soru CD kenarına ait yükseklikle AD kenarına ait yüksekliğin toplamını istediği için:
h_CD + h_AD = 8 + 6 = 14 cm
Yanıtımız: 14 cm (Seçenek A).
1. İçindekiler Tablosu
- Paralelkenara Genel Bakış
- Temel Kavramlar
- Verilenlerin Analizi
- Paralelkenarın Alan Formülü
- CD Kenarına Ait Yükseklik
- AD Kenarına Ait Yükseklik
- Yüksekliklerin Toplamının Hesaplanması
- Adım Adım Çözüm Özeti
- Örnek Benzer Problemler ve Çözüm İpuçları
- Sık Yapılan Hatalar
- Tablo: Kenar Uzunlukları ve Yükseklikler
- Konu Özeti
- Tam Çözümün Kısa Özeti
2. Paralelkenara Genel Bakış
Bir paralelkenar (paralelogram), karşılıklı iki kenar çifti birbirine paralel olan dörtgendir. Temel özellikleri şunlardır:
- Karşılıklı kenarlar eşit uzunluktadır: AB = CD ve BC = AD.
- Karşılıklı açılar eşittir: ∠A = ∠C ve ∠B = ∠D.
- Paralelkenarın alanı, taban seçilen kenarla, ona dik olan yüksekliğin çarpımıyla hesaplanır.
Bu problemde, hangi kenarı “taban” alırsak alalım, alan aynı olduğundan bu özelliği kullanarak farklı kenarlara ait yükseklikleri bulacağız.
3. Temel Kavramlar
- Taban (Base): Paralelkenarın herhangi bir kenarı taban olarak seçilebilir.
- Yükseklik (Height): Seçilen tabana dik olarak inen en kısa mesafe. Bu mesafe, paralelkenarın alanını hesaplamak için kullanılır.
- Alan (Area): Parallelogram için \text{Alan} = \text{(Taban)} \times \text{(Yükseklik)}.
Matematiksel ifadeyle:
\text{Alan} = \text{Taban} \times \text{Yükseklik}
Verilen soruda iki temel kenarı (CD ve AD) ve bunlara dik olan yükseklikleri ele alacağız.
4. Verilenlerin Analizi
Soru metninde:
- Paralelkenar ABCD’nin alanı: 96 cm²
- Bir kenarının uzunluğu: 12 cm (CD kenarı)
- Diğer bir kenarının uzunluğu: 16 cm (AD kenarı)
Dolayısıyla:
- Paralelkenarın alanı ile CD ve AD kenarlarına ait yükseklikler arasında bağlantı kurmamız gerekiyor.
Paralelkenarın ismine bakarsak, genelde şu sırayla gider: A → B → C → D, yani AB ve CD karşılıklı kenarlardır; BC ve AD diğer karşılıklı kenarlardır. Eğer CD = 12 cm ise AB = 12 cm; AD = 16 cm ise BC = 16 cm olacaktır. Her iki durumda da alan gene 96 cm² kalacaktır.
5. Paralelkenarın Alan Formülü
Bir paralelkenarda alan, sıradan bir dikdörtgende olduğu gibi “taban × yükseklik” ifadesiyle bulunur. Fakat tabanla yükseklik, tam olarak dik olmak zorundadır.
Örneğin CD’yi taban alırsak aşağıdaki formülü kullanırız:
\text{Alan} = CD \times h_{CD}
Aynı şekilde AD’yi taban alırsak:
\text{Alan} = AD \times h_{AD}
Burada:
- CD = 12 cm
- AD = 16 cm
- h_{CD} = CD kenarına ait yükseklik
- h_{AD} = AD kenarına ait yükseklik
Toplam alan her iki seçimde de 96 cm²’dir, çünkü paralelkenarın geometrik alanı değişmez.
6. CD Kenarına Ait Yükseklik
Soruda CD kenarına ait yüksekliği “$h_{CD}$” olarak belirtelim. Alan formülünü kullanırsak:
CD \times h_{CD} = 96
Bizim problemde CD = 12 \text{ cm} olduğuna göre:
12 \times h_{CD} = 96
Her iki tarafı 12’ye böldüğümüzde:
h_{CD} = \frac{96}{12} = 8 \text{ cm}
Yani, CD kenarına ait yükseklik 8 cm’dir.
7. AD Kenarına Ait Yükseklik
AD kenarına ait yüksekliği “$h_{AD}$” olarak işaretleyelim. Benzer şekilde alan ifadesi:
AD \times h_{AD} = 96
Bu defa AD = 16 \text{ cm} olduğu için:
16 \times h_{AD} = 96
Her iki tarafı 16’ya böldüğümüzde:
h_{AD} = \frac{96}{16} = 6 \text{ cm}
Böylece, AD kenarına ait yükseklik de 6 cm olarak bulunur.
8. Yüksekliklerin Toplamının Hesaplanması
Soru bizden tam olarak şu değeri istiyor:
“CD kenarına ait yükseklik + AD kenarına ait yükseklik”
Yani:
h_{CD} + h_{AD} = 8 + 6 = 14 \text{ cm}
Bu sonuç soruda verilen doğrultuda bir seçenek olarak 14 cm’dir.
9. Adım Adım Çözüm Özeti
- Alan Bilgisi: Paralelkenarın alanı 96 cm² olarak verilir.
- Kenar Uzunlukları: Soruya göre CD = 12 cm ve AD = 16 cm şeklinde belirlenir.
- CD Kenarını Taban Almak:
- Formül: CD \times h_{CD} = 96
- Hesap: 12 \times h_{CD} = 96 \Rightarrow h_{CD} = 8 \text{ cm}
- AD Kenarını Taban Almak:
- Formül: AD \times h_{AD} = 96
- Hesap: 16 \times h_{AD} = 96 \Rightarrow h_{AD} = 6 \text{ cm}
- Toplam Yükseklik: h_{CD} + h_{AD} = 8 + 6 = 14 \text{ cm}
Bu, soruda aranan cevaba denk gelir.
10. Örnek Benzer Problemler ve Çözüm İpuçları
-
Dikdörtgen İçeren Sorular
- Dikdörtgende taban ve yükseklik zaten kenarlarıdır. Fakat orada tüm yükseklikler kolay tespit edilir.
-
Eğik Dörtgenler
- Paralelkenarda olduğu gibi taban- yükseklik ilişkisini kullanın. Kenar uzunluğu ile dik mesafe çarpımına dikkat edin.
-
Diğer Özel Dörtgenler (Eşkenar Dörtgen vb.)
- Eşkenar dörtgen de aslında paralelkenardır. Yine aynı formülü (taban × yükseklik) kullanırız.
-
Üçgenlere Bölerek Çözüm
- Kimi sorularda paralelkenarı iki üçgene bölebilirsiniz, böylece üçgenin alanı üzerinden tekrar paralelkenara dönüş yapabilirsiniz.
Bu ipuçları, soru çözerken hem alan kavramını pekiştirir hem de farklı varyasyonlar için strateji geliştirmenize yardımcı olur.
11. Sık Yapılan Hatalar
- Yanlış Kenarı Taban Almak: Aslında hangi kenarı alırsanız alın, doğru yüksekliği bulduğunuz sürece sonuç değişmez. Fakat kenar ve yükseklik eşleştirilmesi hatalı yapılırsa sonuç yanlış olur.
- Kenar Uzunlukları İle Yükseklikleri Karıştırmak: Kenar uzunluğu doğrudan “yükseklik” gibi düşünülmemelidir. Yükseklik, tabana dik olan mesafedir.
- Alan Formülünü Yanlış Uygulamak: Alan = taban × yükseklik ilkesinin unutulması ya da karıştırılması.
- Ortak Alan Yanlış Anlamı: Birden fazla kenara göre hesaplanırken alanın aynı kalacağı gözden kaçabilir.
Bu tür hatalar, sınavlarda ve problem çözümünde en sık karşılaşılan durumlardır. Mantıksal olarak aynı alan ifadesini iki farklı taban için kullanınca, iki farklı yükseklik değeri elde edeceğimizi unutmamak gerekir.
12. Tablo: Kenar Uzunlukları ve Yükseklikler
Aşağıdaki tabloda, hangi kenar taban olarak seçildiğinde hangi yükseklik kullanıldığı ve sonuçların nasıl hesaplandığı gösterilmektedir:
| Taban (Base) | Taban Uzunluğu (cm) | Alan (cm²) | Yükseklik (cm) | Yükseklik Hesabı |
|---|---|---|---|---|
| CD | 12 | 96 | h_{CD} = 8 | 12 \times 8 = 96 |
| AD | 16 | 96 | h_{AD} = 6 | 16 \times 6 = 96 |
Tabloya göre h_{CD} + h_{AD} = 8 + 6 = 14.
13. Konu Özeti
- Paralelkenarın temel özelliği: Karşılıklı kenarlar paralel ve eşit uzunlukta.
- Alan, seçilen taban ve bu tabana dik yüksekliğin çarpımıyla elde edilir.
- Bu soru özelinde:
- CD kenarı = 12 cm, ona ait yükseklik = 8 cm.
- AD kenarı = 16 cm, ona ait yükseklik = 6 cm.
- Toplam alan = 96 cm² sabittir.
- İki yüksekliğin toplamı = 14 cm.
Bu bilgiler ışığında doğru cevap 14 cm olarak belirlenir.
14. Tam Çözümün Kısa Özeti
Bir paralelkenarın alanı 96 cm² olup, iki farklı kenarının uzunluğu sırasıyla 12 cm (CD) ve 16 cm (AD) verilmiştir. Kenar ile buna ait yüksekliğin çarpımı alanı verdiğinden,
• CD kenarına ait yükseklik = 96 / 12 = 8 cm
• AD kenarına ait yükseklik = 96 / 16 = 6 cm
İstenen bu iki yüksekliğin toplamıdır:
8 + 6 = 14 cm
Dolayısıyla soru “Buna göre CD kenarına ait yükseklik ile AD kenarına ait yüksekliğin toplamı kaç cm’dir?” diye sorduğunda, 14 cm yanıtına ulaşırız.
Sonuç:
Soruya ait doğru cevap 14 cm’dir.