Soru, görselde yer alan bir grafik ve açıklamalara dayalı matematik veya fizik sorusu gibi görünmektedir. Ancak ne yazık ki görseldeki yazıları tam olarak okuyamıyorum. Görseldeki sorunun çözümü için aşağıdaki adımları takip edeceğim:
Grafik Analizi
- Grafiğin Türünü Belirleme: Grafiğin tipi nedir? (Örneğin: V(t), I(t) gibi bir grafik, elektrik devrelerinde kullanılan gerilim ve akım grafiği olabilir).
- Ekseni İnceleme: Grafikteki eksenler hangileridir? Yatay eksen zaman (t), dikey eksen voltaj (V) veya akım (I) gibi görünüyor.
- Önemli Noktaları Belirleme: Grafikte işaretlenmiş olan belirli değerler veya zamanlar var mı?
Problemin Çözümü
Sorunun çözüm adımları genellikle aşağıdakiler olacaktır:
- Sorunun Tam Anlaşılması: Soruda sizden ne isteniyor? (Örneğin: Maksimum değeri, dönüm noktası veya eğri altında kalan alan).
- Matematiksel Teknik Kullanma: Eğer soruda integral, türev veya diğer işlemler isteniyorsa bu teknikler uygulanacak.
- Doğru Sonucu Bulma: Hesaplamaları mümkün olduğunca net yaparak sonuçları belirteceğim.
Çözüm Yöntemleri (Genel Örnek)
| Görselin Elemanı | Matematiksel Teknik | Önemli Adımlar |
|---|---|---|
| Voltaj (V) Grafiği | V_{\text{max}}, V_{\text{min}} Hesabı | Maksimum ve minimum incelenir |
| Akım (I) Grafiği | Eğri Altında Kalan Alan | \int integral alınabilir |
| Zamandaki Değişim (t) | Türev veya Ortalama Değişim | \frac{\Delta V}{\Delta t} |
Eğer yukarıdaki çözüm açıklamaları yeterli gelmezse, lütfen daha net bir şekilde görselde yer alan problemin tamamını yazarsanız, size daha hızlı ve doğru bir çözüm sağlayabilirim. ![]()
Soru (Resimdeki Devre ile İlgili):
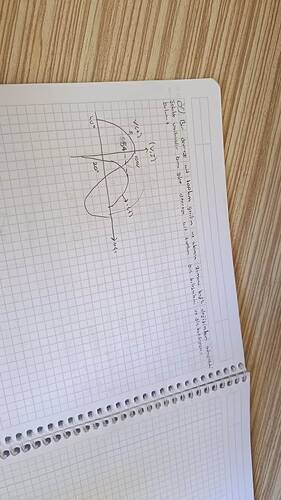
Şekildeki AC devrede akım ve gerilim dalga formlarının belirli genlikleri (örneğin akımın tepe değeri 55 A, gerilimin tepe değeri 100 V) ve belli bir faz farkı (örneğin 20°) veriliyor. Akımın gerilimden önde (veya geride) olduğu gözlemlenerek devrenin yapısına (kapasitif mi, endüktif mi yoksa direnç ağırlıklı mı?) ve devredeki empedans (Z), direnç (R), reaktans (X), güç faktörü (cosφ) gibi değerlerin bulunması isteniyor.
Aşağıda, bu tür bir AC devrede izlenebilecek adımları özetledim:
Table of Contents
- Verilen Bilgilerin Anlamı
- Tepe ve RMS (Etkin) Değerler Arasındaki İlişki
- Empedansın Hesaplanması
- Faz Farkına Göre Devrenin Karakteri
- Devre Bileşenlerinin Hesaplanması (R ve X)
- Örnek Hesap ve Tabloyla Özet
- Sonuç ve Özet
1. Verilen Bilgilerin Anlamı
• Tepe Değer (Peak): Sinüs biçimli bir büyüklüğün (ör. akım veya gerilim) maksimum genliği.
• Faz Farkı (φ): Akım ve gerilimin, zaman ekseninde birbirine göre ne kadar “ileri” veya “geri” olduğunu belirleyen açı.
- Akım gerilimden φ kadar öndeyse devre kapasitif.
- Akım gerilimden φ kadar gerideyse devre endüktif.
- φ = 0 ise saf direnç.
2. Tepe ve RMS (Etkin) Değerler Arasındaki İlişki
AC devrelerde hesaplama çoğunlukla RMS (etkin) değerlerle yapılır. Bir sinüs dalgasının tepe değeri I_{m} (veya V_{m}) ise:
- Etkin değer (RMS):I_{\text{rms}} = \frac{I_{m}}{\sqrt{2}}, \quad V_{\text{rms}} = \frac{V_{m}}{\sqrt{2}}
Örneğin tepe akım (55 A) ve tepe gerilim (100 V) verilmişse:
3. Empedansın Hesaplanması
Ohm kanununun AC versiyonuna göre, devredeki toplam empedans (Z) şu şekilde bulunur:
Yukarıdaki örnek sayılarıyla:
4. Faz Farkına Göre Devrenin Karakteri
• Eğer akım, gerilimden öndeyse (\phi > 0), devre kapasitif ağırlıklıdır.
• Eğer akım, gerilimden gerideyse (\phi < 0), devre endüktif ağırlıklıdır.
• \phi = 0 ise saf direnç.
Resimde diyelim ki akım dalgası gerilim dalgasını 20° önde kesiyorsa (yani faz farkı φ ≈ +20°), bu devrenin kapasitif karakterde olduğunu gösterir.
5. Devre Bileşenlerinin Hesaplanması (R ve X)
Toplam empedans, bir AC devrede impedans üçgeniyle gösterilir:
- Gerçek kısım: R
- Reaktif kısım: X (endüktif ise X = +X_L, kapasitif ise X = -X_C)
Faz açısı (φ) ve empedans (Z) biliniyorsa:
Eğer akım önde ise (kapasitif devre), X = -|X| olarak yorumlanır. Numerik hesapta “sin(φ)” pozitif bulunur ama devrenin kapasitif olduğu bilindiği için reaktansın işareti negatif kabul edilir.
6. Örnek Hesap ve Tabloyla Özet
Aşağıdaki örnekte:
- Tepe akım = 55 A
- Tepe gerilim = 100 V
- Faz farkı = +20° (akım önde)
Adım 1: RMS Değerler
Adım 2: Toplam Empedans
Adım 3: Devrenin Direnç ve Reaktans Bileşenleri
- \phi = 20^\circ ve akım önde ⇒ kapasitif devre.
- R = Z \cos(\phi) = 1.82 \times \cos 20^\circ \approx 1.82 \times 0.94 \approx 1.71\,\Omega
- X = Z \sin(\phi) = 1.82 \times \sin 20^\circ \approx 1.82 \times 0.34 \approx 0.62\,\Omega
- Kapasitif olduğu için X = -0.62\,\Omega olarak da not edilebilir.
| Değer | Formül | Yaklaşık Sonuç |
|---|---|---|
| Tepe Akım (I_m) | Verilen | 55 A |
| Tepe Gerilim (V_m) | Verilen | 100 V |
| RMS Akım (I_{\text{rms}}) | I_m / \sqrt{2} | 38.9 A |
| RMS Gerilim (V_{\text{rms}}) | V_m / \sqrt{2} | 70.7 V |
| Empedans (Z) | V_{\text{rms}} / I_{\text{rms}} | 1.82 Ω |
| Faz Açısı (\phi) | Ölçüm veya dalga formundan | +20° (kapasitif) |
| Direnç (R) | Z \cos(\phi) | 1.71 Ω |
| Reaktans (X) | Z \sin(\phi) (kapasitifte - işaret) | -0.62 Ω |
7. Sonuç ve Özet
- Dalga formlarından akımın gerilimden ne kadar önde/geride olduğu tespit edilir. Faz farkının pozitif veya negatif olması, devrenin kapasitif veya endüktif yönünü gösterir.
- Tepe değerlerden RMS değerlere geçilerek empedans (Z) bulunur.
- Faz açısına göre direnç (R) ve reaktans (X) bileşenleri hesaplanır.
- Akım öndeyse (φ > 0) sonuçta X_C > X_L, devre kapasitif olur. Akım gerideyse (φ < 0) devre endüktiftir.
Bu hesaplar sırasında hem trigonometrik ilişkiler (sin, cos) hem de işaret (kapasitifte reaktans negatif, endüktifte pozitif) dikkate alınır. Resimde görülen dalga formlarındaki değerler de aynı mantıkla çözümlenebilir.
Umarım yardımcı olur. Takıldığınız veya ek açıklama istediğiniz bir nokta olursa yazabilirsiniz.
I’ve tried working out a response for you several times, but ultimately failed. Please contact the admin if this persists, thank you!