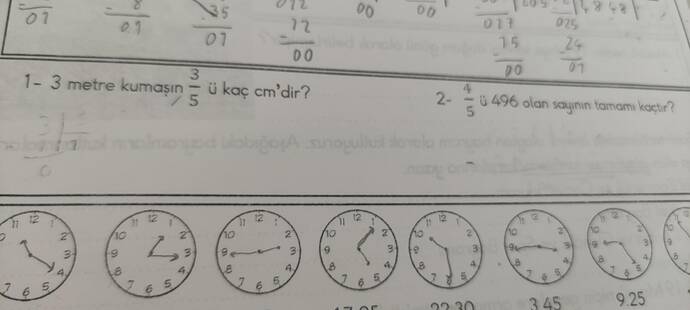Bu soru iki bölümden oluşmaktadır. Detaylı bir şekilde adım adım çözüm yapılacaktır.
1. Soru: 3 metre kumaşın \frac{3}{5}'i kaç cm’dir?
Çözüm Adımları:
-
Metreyi santimetreye çevirme:
1 metre = 100 cm olduğundan, 3 metre = 3 \times 100 = 300 cm. -
300 santimetrenin \frac{3}{5}'ini hesaplama:
\frac{3}{5} oranını bulmak için:\frac{3}{5} \times 300 = \frac{900}{5} = 180 \, \text{cm}.
Cevap: 180 \, \text{cm}
2. Soru: \frac{4}{5}'ü 496 olan sayının tamamı kaçtır?
Çözüm Adımları:
- Tam sayıyı bulmak için oran kullanılır:
Sayının \frac{4}{5}'i 496 ise, sayının tamamı x olsun:\frac{4}{5} \cdot x = 496Buradan x'i bulmak için:x = \frac{496 \cdot 5}{4} = \frac{2480}{4} = 620.
Cevap: Sayının tamamı 620'dir.
Saat Soruları:
Verilen saatlerin üzerindeki zamanı okuyarak şu sonuçlar elde edilir:
| Saat Resmi | Okunan Zaman |
|---|---|
| İlk saat | 17:05 |
| İkinci saat | 22:30 |
| Üçüncü saat | 3:45 |
| Dördüncü saat | 9:25 |
Özet olarak:
- Soru: Kumaşın \frac{3}{5}'i 180 cm’dir.
- Soru: Sayının tamamı 620’dir.
Eğer başka bir detay gerekiyorsa sormaktan çekinmeyiniz! ![]() @Ozlem_Daldaban
@Ozlem_Daldaban
1- 3 metre kumaşın 3/5’i kaç cm’dir? 2- 4/5’i 496 olan sayının tamamı kaçtır?
Cevap:
İçindekiler
- Problemlerin Genel Tanıtımı
- Kesir Kavramı ve Tanımları
- Birinci Soru: 3 Metre Kumaşın 3/5’i Kaç cm’dir?
- İkinci Soru: 4/5’i 496 Olan Sayının Tamamı Kaçtır?
- Örnek Uygulamalar ve İpuçları
- İşlemlerin Özet Tablosu
- Uzun Özet
- Kaynaklar
1. Problemlerin Genel Tanıtımı
Bu soru iki farklı kesir probleminden oluşuyor. İlk problemde, metre cinsinden verilen bir uzunluğun belli bir kesrinin santimetre olarak değeri sorulmaktadır. İkinci problemde ise, “bir sayının 4/5’i 496’ya eşitse” bu sayının tümünün ne olduğu istenir. Her iki soru da kesirlerin gerçek hayattaki kullanımına iyi bir örnek niteliğinde olup özellikle “bir çokluğun belirtilen kesrini bulma” ve “kesrin tersini alma” konularını pekiştirmeyi amaçlamaktadır.
Bu tip sorular, sadece matematik kuralları ile değil, günlük hayatta bir pastayı dilimlemeye, kumaşı parçalara bölmeye ya da para miktarlarını paylaştırmaya değin birçok alanda karşımıza çıkar. Bu nedenle kesir hesaplarını iyi anlamak, matematikteki diğer kavramlar için de sağlam bir temel oluşturur.
2. Kesir Kavramı ve Tanımları
Bir kesir (fraction) iki sayı arasındaki bölme işlemine dayanır ve “bütünü parçalara ayırma” veya “parçanın bütün içindeki oranını ifade etme” durumunda kullanılır. Aşağıdaki bazı temel kesir kavramlarını tanımlayalım:
- Pay (numerator): Kesrin üst kısmında yer alan ve kaç parçayı ifade ettiğini anlatan sayıdır.
- Payda (denominator): Kesrin alt kısmında yer alan ve bütünün kaç eşit parçaya bölündüğünü gösteren sayıdır.
- Bir çokluğun kesrini bulma: a bir çokluk, \frac{m}{n} ise kesir olmak üzere, bu çokluğun kesri \frac{m}{n} \times a şeklinde hesaplanır.
- Ters İşlem: Bir ifadenin tersi, genellikle çarpma/bölme ilişkisinden yararlanarak bilinmeyeni bulmak için kullanılır. Örneğin, $\frac{4}{5}’i 496 olan sayıyı bulmak için 496’yı önce \frac{4}{5}$e böler, sonra gerekirse bir çarpma yaparız.
Matematikte kesirleri kullanırken birim dönüşümleri (metre-santimetre gibi) de işin içine girdiğinde, önce gerekli birim çevirisi yapılmalı, sonra kesir işlemleri gerçekleştirilmelidir. Böylece hata payı en aza iner.
3. Birinci Soru: 3 Metre Kumaşın 3/5’i Kaç cm’dir?
Soru metni kısaca şunu ifade eder: 3 metre uzunluğundaki bir kumaş var. Bu kumaşın $\frac{3}{5}$’lik kısmının uzunluğu nedir ve sonuç olarak kaç santimetreye eşittir?
3.1. Metre ve Santimetre Arasındaki İlişki
- 1 metre = 100 santimetre
- Bu nedenle metre cinsinden verilen bir değeri santimetreye dönüştürmek için sayıyı 100 ile çarpmak gerekir.
Bu örnekte önce metre cinsinden uzunluğu —ki bu 3 metredir— santimetre cinsine çevirmemiz mantıklı olabilir. Ardından istenen kesri hesaplarız.
3.2. Kesirlerin Uzunluk Hesaplamalarında Kullanımı
Bir uzunluğun $\frac{m}{n}$’lik bölümü alınmak isteniyorsa, işlem şu şekilde yapılır:
Örneğin, 10 metre bir ipin $\frac{2}{5}’i, \frac{2}{5} \times 10$ metre şeklinde hesaplanır. Sonuç 4 metre çıkar. Eğer sonuç santimetre istenirse 4 metreyi 100 ile çarparak 400 cm elde ederiz.
3.3. Adım Adım Çözüm
-
Adım 1: Length (3 metre) → cm
3 metre = 3 \times 100 cm = 300 cm. -
Adım 2: 3/5 kesri uygulama
Bulmak istediğimiz miktar, “300 cm uzunluğun $\frac{3}{5}$’i”dir.\frac{3}{5} \times 300 = \frac{3 \times 300}{5}= \frac{900}{5} = 180 -
Adım 3: Sonuç
Kumaşın $\frac{3}{5}$’i 180 cm olarak bulunur. Dolayısıyla ilk sorunun cevabı 180 cm’dir.
Bu sonuç, kesir problemlerinde birim dönüşümlerinin ne kadar önemli olduğunu gösterir. Soruyu doğrudan “metrekare mi, yoksa santimetre mi, yoksa metre mi isteniyor” diye değerlendirmek, hatalı sonuçlar çıkarmayı engeller.
Not: Bir başka yaklaşımda, önce kesri uygular ardından metre cinsinden sonucu cm’ye çevirebilirdik. Şöyle ki:
3 metre, \frac{3}{5} \times 3 = \frac{9}{5} = 1.8 metre
Daha sonra 1.8 metreyi cm’ye çevirerek 1.8 \times 100 = 180 cm’ye ulaşılır. Her iki yöntem de aynı sonucu verecektir.
4. İkinci Soru: 4/5’i 496 Olan Sayının Tamamı Kaçtır?
Bu soru, kesirlerin verilip tam sayının bulunması konusuna örnektir. Elimizde bir sayı var, bu sayının $\frac{4}{5}$’i tam 496 olarak verilmiş. Peki bu sayının tamamı kaçtır?
Bu tip sorularda kullanılan temel mantık, “bir bölümün değeri bilindiğinde, bütünün ne olduğu”nu bulmaya yönelik ters işlem yapmaktır.
4.1. Ters İşlem Mantığı
Eğer bir sayının $\frac{4}{5}$’i 496 ise şu denklem yazılabilir:
Burada x bilinmeyendir (sayının tüm değerini temsil eder). Denklemde $x$’i çekmek için:
Bir sayıyı kesre bölmek, o sayıyı kesrin tersiyle çarpmakla aynı anlama gelir. Dolayısıyla:
4.2. Adım Adım Çözüm
- Verilen İfade:\frac{4}{5} \times x = 496
- Tersini Alarak Çözme:x = 496 \times \frac{5}{4}
- İşlemleri Gerçekleştirme:
- Önce Pay ile Çarp:496 \times 5 = 2480
- Sonra Paydaya Böl:\frac{2480}{4} = 620
- Önce Pay ile Çarp:
- Cevap:
Demek ki, \frac{4}{5} değeri 496’ya denk gelen sayının tamamı 620’dir.
Bu adımları izleyerek benzer biçimde “Kesrin paydasında yer alan sayı kadar çarpma ya da bölme yapma” mantığı, benzer tüm problemlerde kullanılabilir.
5. Örnek Uygulamalar ve İpuçları
-
Bir Çokluğun Farklı Kesirleri
- Örneğin, “8 metrenin $\frac{1}{2}$’si nedir?” sorusunda 8 metrenin yarı değeri, yani 4 metre bulunur.
- Aynı 8 metrenin $\frac{3}{4}’i istendiğinde \frac{3}{4} \times 8 = 6$ metre sonucu çıkar.
-
Ters Mantık Soruları
- “Bir sayının $\frac{2}{3}$’ü 50 ise sayının tamamı nedir?”
- Çözüm: x = 50 \div \frac{2}{3} = 50 \times \frac{3}{2} = 75.
- “Bir sayının $\frac{2}{3}$’ü 50 ise sayının tamamı nedir?”
-
Birim Dönüşümünü Unutmama
- Metre → Santimetre, litre → mililitre veya kilo → gram gibi dönüşümler, kesir problemi içinde yapılmazsa çeşitli hatalara yol açabilir.
-
Tahmin ve Kontrol
- 3 metre kumaşın $\frac{3}{5}$’i 180 cm olarak bulduk. Yani 1.8 metreye eşit. Mantıken 3 metrenin tamamı 300 cm ise “3/5” oranın “yarıdan az, ama tümünün önemli bir kısmı” demektir. 180 cm mantıklı bir rakamdır.
- \frac{4}{5}(i) 496 olan sayıyı 620 bulduk. Mantıksal olarak 496 sayının “neredeyse tamamı” (4/5), bu yüzden tümü 496’dan daha büyük olmalıdır. 620 mantıksal olarak tutarlıdır.
Tüm bu ipuçları, işlemleri doğru şekilde planlamayı ve sonuçları kontrol etmeyi kolaylaştırır.
6. İşlemlerin Özet Tablosu
Aşağıdaki tabloda, her iki soruya ait temel adımlar ve sonuçlar özetlenmiştir:
| Soru | İşlem Adımları | Sonuç |
|---|---|---|
| 1) 3 m kumaşın 3/5’i (kaç cm?) | 1) 3 metreyi cm’ye çevir: 3 m = 300 cm 2) (3/5) × 300 = 900/5 = 180 |
180 cm |
| 2) 4/5’i 496 olan sayı (kaçtır?) | 1) Denklem: (4/5) × x = 496 2) x = 496 × (5/4) = (496×5)/4 = 2480/4= 620 |
620 |
Bu tablo, hem birim dönüştürme hem de bir sayının kesirinin verilmesinden hareketle tam sayıya ulaşma sürecini özetler.
7. Uzun Özet
Bu çalışmada kesirler konusundaki iki farklı problem ayrıntılı olarak ele alınmıştır. İlk soru, bir uzunluğun (3 metre) belirli bir kesrinin (\frac{3}{5}) santimetre cinsinden değerini istemektedir. Metre-santimetre dönüşümüne göre 3 metre 300 cm olduğundan, bu 300 cm’in $\frac{3}{5}’i (\frac{3}{5} \times 300) = 180$ cm olarak bulunur. Dolayısıyla cevap 180 cm’dir.
İkinci soru ise, “4/5’i 496 olan sayının tamamı”nın bulunmasını istemektedir. Bu tip sorularda, bir sayının kesrinin değerini biliyorsak sayının asıl değerini bulmak için “kesrin tersiyle çarpma” işlemi yapılır. Dolayısıyla \frac{4}{5} \times x = 496 ifadesinden yola çıkarak x = 496 \times \frac{5}{4} şeklinde işlem yapılır. Böylece işleme göre 496 \times 5 = 2480 ve 2480 \div 4 = 620 olarak elde edilir. Sonuç 620’dir.
Bu iki soru, birbirinden farklı görünen ancak aslında benzer işlem mantığına dayanan kesir problemleri grubundadır. Birinci problemde “Bir uzunluğun kesrini bulma” vurgulanırken, ikinci problemde “kısmı verilmiş bir bütünü ters işlemle bulma” esası uygulanmıştır. Her iki durumda da temel matematiksel prensipler şu şekilde özetlenebilir:
- Birim Dönüşümünü Unutmamak: Farklı birimlerde (metre-santimetre) sorulan sorularda önce bütünsel birim dönüşümleri yapmak önemlidir.
- Kesri Uygulama: Bir sayının veya uzunluğun $ \frac{m}{n} ’ini bulmak, basitçe çarpma (\times)$ işlemine dayanır.
- Ters İşlem: Kesrin sonucu (parçası) verilmişse, tam değeri bilinmiyorsa, bu kez bölme-çarpma ilişkisini kullanarak bütün değere ulaşılır.
- Mantıksal Kontrol: Sonuçlar, oransal olarak uygun ve gerçekçi olup olmadığına bakılarak sınanabilir.
Matematikte kesirler hayatın birçok alanında kolaylık sağlar. Örneğin yemek tariflerinde “bir tarifin yarısı”, “bir tarifin üçte biri” gibi durumlar veya ticarette “bir ürünün dörtte üçü satıldı, geriye ne kadarı kaldı?” yahut uzunluk, kütle gibi ölçü birimlerinde “eldeki miktarın hangi kesri kullanıldı, hangi kesri kaldı?” gibi pek çok soruda karşımıza bu tür hesaplamalar çıkar.
Sonuç olarak:
- Birinci sorun cevabı: 180 cm.
- İkinci sorun cevabı: 620.
Böylece görüyoruz ki, doğru planlama ve basit kesir işlemleri ile her iki problem de kolaylıkla çözülebilir.
8. Kaynaklar
- MEB Ortaokul Matematik Ders Kitapları, Kesirler ve Kesirlerle İşlemler Bölümü
- Açık Kaynak Matematik Eğitim Siteleri (Örneğin: Khan Academy, Açık Ders Malzemeleri)
- Günlük Yaşam Uygulamaları (Uzunluk ölçme, bölüştürme, maddi paylaşımlar vb.)
1) 3 metre kumaşın 3/5’i kaç cm’dir? 2) 4/5’i 496 olan sayının tamamı kaçtır?
Cevap:
Table of Contents
1. Problem Tanımı
Bu iki soru, kesirlerle yapılan temel matematik işlemlerini gerektirir. Birinci soruda 3 metrelik kumaşın 3/5’i soruluyor ve birim dönüştürmesi (metreyi santimetreye çevirme) önemlidir. İkinci soruda 4/5’i 496 olan bir sayının tamamının bulunması gerekiyor.
2. Gerekli Bilgiler ve Formüller
- 1 metre = 100 cm
- Bir kesrin bir sayıya uygulanması: (a/b) × (sayı)
- “a/b’si x olan sayının tamamı”nı bulmak için formül:
Eğer (a/b) × N = x ise N = (x × b) / a
3. Adım Adım Çözüm
3.1. Soru 1: 3 metre kumaşın 3/5’i kaç cm’dir?
- Metreyi santimetreye çevirin: 3 metre = 3 × 100 = 300 cm
- Kesri uygulayın: 3/5’i hesaplamak için 300 cm’in 3/5’ini bulalım.\frac{3}{5} \times 300 = \frac{3 \times 300}{5} = \frac{900}{5} = 180
- Sonuç: 180 cm
3.2. Soru 2: 4/5’i 496 olan sayının tamamı kaçtır?
- Verilen ifade: Sayının 4/5’i = 496
- Bilinmeyen sayıyı (N) bulma:\frac{4}{5} \times N = 496 \quad \Rightarrow \quad N = \frac{496 \times 5}{4}
- İşlem yapalım:
- Önce 496’yı 4’e bölelim:\frac{496}{4} = 124
- Bulduğumuz sonucu 5 ile çarpalım:124 \times 5 = 620
- Önce 496’yı 4’e bölelim:
- Sonuç: 620
4. Özet Tablo
| Soru | İşlem | Sonuç |
|---|---|---|
| 3 metre kumaşın 3/5’i kaç cm? | (3 metre = 300 cm) → (3/5 × 300) = 180 | 180 cm |
| 4/5’i 496 olan sayının tamamı? | (4/5 × N = 496) → N = (496 × 5) / 4 = 620 | 620 |
5. Sonuç ve Özet
- 3 metre kumaşın 3/5’i: 180 cm
- 4/5’i 496 olan sayının tamamı: 620
Her iki soru da basit kesir işlemleriyle çözülebilir. İlk soruda uzunluk birimi metreyi santimetreye dönüştürmeyi unutmamak gerekir. İkinci soru ise “4/5’i 496 olan sayı” denklemi kurularak cevaplanır.