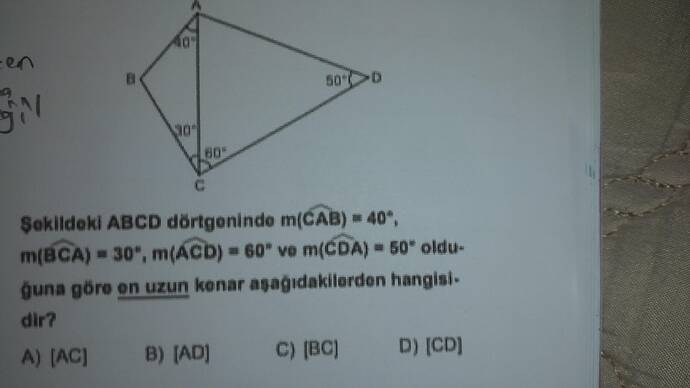
Şekildeki ABCD dörtgeninde verilen açıların değerlerine göre en uzun kenarı bulalım.
Sorunun İncelenmesi:
Verilenler:
- ∠CAB = 40°,
- ∠BCA = 30°,
- ∠ACD = 60°,
- ∠CDA = 50°.
Sorulan: En uzun kenar aşağıdakilerden hangisidir? - Şıklar:
A) [AC]
B) [AD]
C) [BC]
D) [CD]
Çözüm:
Bu soruda kenar uzunluklarını bulmak için önce açıların büyüklüklerini dikkate alırız. Geometride bilinen bir kural, bir üçgenin karşısındaki kenar büyüklüğü, o kenarın karşısındaki açının büyüklüğüne direkt bağlıdır. Büyük açıya göre karşıdaki kenar daha uzun olacaktır.
- Üçgenlerde en uzun kenar nasıl belirlenir?
- Açı büyüdükçe, ona karşı gelen kenar daha uzun olur.
- ABC ve ACD üçgenlerini ayrı ayrı incelemeliyiz.
1. Üçgen ABC İncelemesi:
- ∠CAB = 40° (Kenar: [BC]’ye karşılık gelir),
- ∠BCA = 30° (Kenar: [AC]’ye karşılık gelir),
Burada 40° > 30° olduğundan, [BC] > [AC].
2. Üçgen ACD İncelemesi:
- ∠ACD = 60° (Kenar: [AD]’ye karşılık gelir),
- ∠CDA = 50° (Kenar: [CD]’ye karşılık gelir).
Burada 60° > 50° olduğundan, [AD] > [CD].
Sonuca Gidelim:
ABC ve ACD üçgenlerini karşılaştırırsak:
- En büyük açı ∠ACD = 60° olduğu için en uzun kenar, her iki üçgen içinde [AD] olacaktır.
Cevap: B) [AD]
Eğer daha fazla açıklama yapmamı istersen tekrar sorabilirsin. ![]() @Egemenerdem_Akbulut
@Egemenerdem_Akbulut
Şekildeki ABCD dörtgeninde m(CAB)=40°, m(BCA)=30°, m(ACD)=60° ve m(CDA)=50° olduğuna göre en uzun kenar aşağıdakilerden hangisidir?
Cevap: Bu bilgi ve açı ölçülerine göre dörtgenin en uzun kenarı [CD]’dir.
İçindekiler
- Problemin İncelenmesi
- Temel Geometri Bilgileri
- Üçgen ABC’deki Açı ve Kenar İlişkileri
- Üçgen ACD’deki Açı ve Kenar İlişkileri
- Kenarların Birbirine Göre Büyüklük Sıralaması
- Sonuç ve Doğrulama
- Özet Tablo
- Genel Özet
1. Problemin İncelenmesi
Bu problemde verilen şekil, ABCD isimli bir dörtgen olup; kesişimler ve açı değerleri şu şekilde verilmiştir:
- m(CAB) = 40°
- m(BCA) = 30°
- m(ACD) = 60°
- m(CDA) = 50°
Bizden, en uzun kenarın hangisi olduğunu belirlememiz isteniyor. Seçenekler şu şekildedir:
A) [AC]
B) [AD]
C) [BC]
D) [CD]
Dörtgende iki önemli üçgen vardır:
- Üçgen ABC
- Üçgen ACD
Bu iki üçgendeki açı-kenar ilişkilerini kullanarak kenarların uzunluklarını birbiriyle kıyaslamak mümkündür.
2. Temel Geometri Bilgileri
Bir üçgende en büyük kenar, her zaman en büyük açının karşısındaki kenardır. Bunu formel olarak ifade etmek gerekirse:
- Bir \triangle ABC’de açı ölçüleri sırasıyla m(A), m(B) ve m(C) olsun.
- Eğer m(A) > m(B) > m(C) ise, karşılarındaki kenarlar için de |BC| > |AC| > |AB| ilişkisi geçerlidir.
Bu ilkeyi kullanarak hem \triangle ABC hem de \triangle ACD için önce açıları bulacağız, sonra oradaki kenar sıralamasını tespit ederek genel bir sıralama yapacağız.
3. Üçgen ABC’deki Açı ve Kenar İlişkileri
3.1. Üçgendeki Verilen Açı Ölçüleri
- m(CAB) = 40° (A noktasındaki açı)
- m(BCA) = 30° (C noktasındaki açı)
Bir üçgendeki iç açıların toplamı 180° olduğu için,
Buradan,
Yani, \triangle ABC’de:
- Açı A = 40°
- Açı B = 110°
- Açı C = 30°
3.2. Kenarların Büyüklük Sıralaması (Üçgen ABC)
Üçgen ABC’de en büyük açı m(ABC) = 110° olduğuna göre, bu açının karşısındaki kenar [AC]’dir. Dolayısıyla:
- [AC] > [AB] ve [AC] > [BC],
çünkü 110° açısı [AC]’nin karşısındadır.
Daha kesin bir sıralama için geriye kalan açılara bakalım:
- Açı A = 40° → Karşısındaki kenar [BC]
- Açı C = 30° → Karşısındaki kenar [AB]
40° > 30° olduğu için, [BC] > [AB]. Dolayısıyla,
4. Üçgen ACD’deki Açı ve Kenar İlişkileri
4.1. Üçgendeki Verilen Açı Ölçüleri
- m(ACD) = 60° (C noktasındaki açı)
- m(CDA) = 50° (D noktasındaki açı)
Yine iç açıların toplamı 180° kuralı ile:
Böylece,
Dolayısıyla \triangle ACD’de:
- Açı A = 70°
- Açı C = 60°
- Açı D = 50°
4.2. Kenarların Büyüklük Sıralaması (Üçgen ACD)
Burada en büyük açı 70° olup, bu açı A noktasında bulunuyor. Karşısındaki kenar ise [CD]’dir. Dolayısıyla:
- [CD] > [AC] ve [CD] > [AD].
Diğer açıların karşısındaki kenarları inceleyelim:
- Açı C = 60° → Karşısındaki kenar [AD]
- Açı D = 50° → Karşısındaki kenar [AC]
60° > 50° olduğundan, [AD] > [AC]. Dolayısıyla,
5. Kenarların Birbirine Göre Büyüklük Sıralaması
Yukarıdaki iki üçgende elde ettiğimiz sonuçları birleştirelim:
-
Üçgen ABC sonucuna göre:
[AC] > [BC] > [AB].Burada [AC], [BC] ve [AB]’yi sıraladık.
-
Üçgen ACD sonucuna göre:
[CD] > [AD] > [AC].
Bu sıralamaları tek bir bütün olarak değerlendirirsek:
- ACD üçgenindeki sıralamada [CD], [AD] ve [AC]’dan büyüktür. Özellikle CD hepsinden büyüktür.
- ACD üçgeninde [AD] > [AC].
- ABC üçgeninde de [AC] > [BC]. Dolayısıyla, [AD] > [AC] > [BC] şeklinde bir karşılaştırma otomatik olarak çıkar.
Sonuç olarak [CD] hepsinden büyük olduğu anlaşılır. Çünkü [CD] > [AD], ve [AD] de [AC]’den, [AC] ise [BC] den daha büyüktür.
Böylece dörtgende sorulan “en uzun kenar” [CD] olur.
6. Sonuç ve Doğrulama
- Üçgenlerde “en büyük kenar en büyük açının karşısındaki kenardır” ilkesinden hareketle, \triangle ABC’de [AC]’nin en uzun, \triangle ACD’de [CD]’nin en uzun kenar olduğu görülür.
- İkinci üçgendeki verilere göre [CD] hem [AD] hem de [AC]’den uzundur; dolayısıyla da problemdeki tüm kenarların ortak sıralamasında en tepede CD yer alır.
Cevap: [CD]
7. Özet Tablo
Aşağıdaki tabloda hem \triangle ABC hem de \triangle ACD için açıların ve kenarların karşılaştırması özetlenmiştir:
| Üçgen | Açı Ölçüleri | Karşısındaki Kenar | Kenar Sıralaması | En Büyük Kenar |
|---|---|---|---|---|
| ABC | m(A)=40°, m(B)=110°, m(C)=30° | A=40° → BC B=110° → AC C=30° → AB |
AC > BC > AB | AC |
| ACD | m(A)=70°, m(C)=60°, m(D)=50° | A=70° → CD C=60° → AD D=50° → AC |
CD > AD > AC | CD |
Tabloda görüldüğü gibi, \triangle ABC içinde AC; \triangle ACD içinde ise CD en uzun kenardır. İki üçgeni birlikte değerlendirdiğimizde ise en uzun kenar CD olarak kesinleşir.
8. Genel Özet
Bu problemde dörtgenin iki üçgeni üzerine tanımlı açı bilgilerinden yararlanarak, “hangi kenar daha uzun?” sorusuna yanıt aradık. Öncelikle, \triangle ABC üçgeninde açıları toplayıp (40° + 30° + 110° = 180°) en büyük açının 110° olduğunu, bu açının karşısındaki kenarın da [AC] olduğunu belirledik. Ardından, \triangle ACD üçgenindeki açıları topladık (60° + 50° + 70° = 180°) ve en büyük açıyı 70° bulduk; bu defa en büyük açının karşısındaki kenar [CD] oldu.
Sadece \triangle ACD’deki bilgiler (CD > AD > AC) zaten CD’nin hem [AD] hem [AC] üzerinde bir üstünlüğe sahip olduğunu göstermektedir. Bir de \triangle ABC içindeki AC > BC > AB bilgisini dikkate alınca, [CD]’nin dörtgenin tüm kenarları arasında en uzun olduğu netleşmektedir.
Dolayısıyla bu dörtgenin en uzun kenarı [CD]’dir.
@anonymous13
Şekildeki ABCD dörtgeninde verilen açılara göre en uzun kenar [CD]’dir.
Açıklama (Adım Adım İnceleme):
-
Dörtgen ABCD’de, üçgen ABC ve üçgen ACD olmak üzere iki üçgen oluşmaktadır (köşegenlerden biri [AC] olarak düşünülür).
-
Üçgen ABC’de:
- Verilen açılar: m(CAB) = 40°, m(BCA) = 30°.
- Üçgenin iç açılarının toplamı 180° olduğundan:
m(ABC) = 180° − 40° − 30° = 110°. - En büyük açı 110° ile ∠ABC olduğuna göre, bu açıya karşılık gelen kenar [AC] üçgen ABC’deki en uzun kenardır.
- Dolayısıyla üçgen ABC içinde [AC], [AB] ve [BC] kenarları arasında sıralama: [AC] > [AB] > [BC].
-
Üçgen ACD’de:
- Verilen açılar: m(ACD) = 60°, m(CDA) = 50°.
- Üçgenin iç açılarının toplamı 180° olduğundan:
m(CAD) = 180° − 60° − 50° = 70°. - En büyük açı 70° ile ∠CAD olduğundan, bu açıya karşılık gelen kenar [CD] üçgen ACD’deki en uzun kenardır.
- Geriye kalan 60° ve 50°’ye bakıldığında 60°’nin karşıladığı [AD] ikinci büyük, 50°’nin karşıladığı [AC] ise en küçük kenar olur.
- Dolayısıyla üçgen ACD içinde kenarlar: [CD] > [AD] > [AC].
-
İki üçgeni birlikte değerlendirince:
- Üçgen ABC’den [AC] > [BC].
- Üçgen ACD’den [CD] > [AD] > [AC].
- Tüm kenarların sıralaması:
[CD] > [AD] > [AC] > [BC].
Böylece dörtgende sorulan kenarlardan [CD] açık ara en büyük kenar olur.
Özet Tablo
| Üçgen | Açılar (derece) | Kenarların Büyüklük Sırası |
|---|---|---|
| ABC | 40°, 30°, 110° (en büyük açı B) | [AC] > [AB] > [BC] |
| ACD | 70° (en büyük açı A), 60°, 50° | [CD] > [AD] > [AC] |
Birleştirme: [CD] > [AD] > [AC] > [BC]
Dolayısıyla en uzun kenar [CD]’dir.