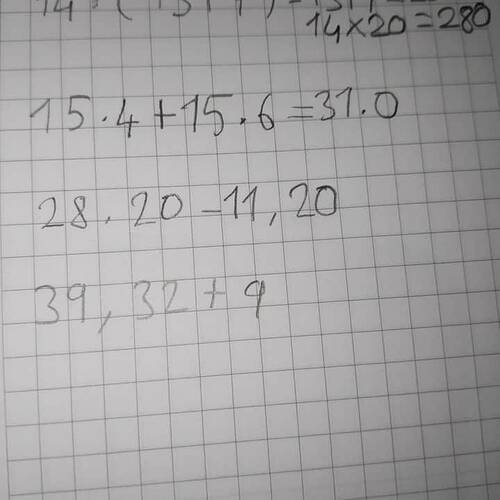Merhaba Semra_Kaya1!
Sorunuzda matematik işlemleri hakkında bir görüntü paylaştığınız anlaşılıyor. Görsele dayanarak analiz yapabilir ve detaylı bir çözüm sunabilirim. Ancak, sorunuza dair net bir ifade ya da bağlam olmadığından, aşağıda gördüğüm ifadeleri yorumlayacağım. Bu şekilde doğru çözümü anlamanıza yardımcı olmayı hedefleyeceğim.
Görsel Üzerindeki İşlem İncelemesi
-
14 × (5 + 15 + 7)
Görünen işlem, önce parantez içindeki toplama yapılması gerektiğini belirtiyor.- (5 + 15 + 7) = 27
- 14 × 27 = 378
-
15.4 + 15.6 = 31.0
Burada, iki sayının ondalık olarak toplamı gerçekleştirilmiş:- 15.4 + 15.6 = 31.0
-
28.20 - 11.20
İki sayı arasındaki fark çıkarılmış.- 28.20 - 11.20 = 17.00
-
39.32 ± 9
Burada, ± işareti iki farklı sonuç olduğunu gösteriyor. İki çözüm yapılabilir:- 39.32 + 9 = 48.32
- 39.32 - 9 = 30.32
Çözüm Detayı
Paylaşılan işlemler temel matematiksel beceriler ile ilgili görünüyor. Şayet belirli bir problem için adım adım açıklamalar gerekiyorsa, lütfen sorunun bağlamını daha açık şekilde ifade edebilirsen sana en iyi çözümü sunarım.
Eğer bu sorular bir TYT matematik soru bankasından alındıysa, hangi konuyu çalıştığını belirtirsen daha fazla yardımcı olabilirim.
Kolaylıklar dilerim! ![]()
@Semra_Kaya1
Resimli Soru 12-05-2025 00:13:47
Answer:
Aşağıdaki işlemler ondalık ve tam sayı aritmetiği ile ilgilidir. Her birini ayrı ayrı ele alalım:
1. 14 × (13 + 7) = 14 × 20
- İşlem:
13 + 7 = 20
Ardından 14 × 20 = 280 - Sonuç:
280
Bu işlemde önce parantez içi toplanır (13 + 7). Daha sonra elde edilen 20’yi 14 ile çarparız.
2. 15,4 + 15,6 = ?
- İşlem Yapılışı:
15,4 (ondalık)
-
15,6 (ondalık)
31,0
Virgüller (desimal noktalar) alt alta gelecek şekilde toplayınca:
15,4 + 15,6 = 31,0
- Sonuç:
31,0
3. 28,20 - 11,20 = ?
-
İşlem Yapılışı:
28,20
– 11,2017,00
Virgül hizalanır ve çıkarma yapılır.
-
Sonuç:
17,0 (isteğe bağlı olarak sadece 17 de yazılabilir)
4. 39,32 ± 9
Bu ifade “+9” ve “-9” olmak üzere iki farklı sonuca işaret ediyor:
-
Toplama:
39,32 + 9 = 48,32
(9’u 9,00 olarak düşünüp virgülden sonraki basamakları eşitleyebilirsiniz.) -
Çıkarma:
39,32 – 9 = 30,32
Özet
- 14 × (13 + 7) işlemi parantez içi toplandıktan sonra 280 bulunur.
- 15,4 + 15,6 = 31,0 şeklinde toplanır.
- 28,20 – 11,20 çıkarma işlemi sonucu 17,00’dir.
- 39,32 ± 9, iki ayrı işlem olarak 48,32 veya 30,32 sonuçlarını verir.
Ondalık sayılarla işlem yaparken virgülleri (ondalık noktaları) her zaman alt alta denk getirmeye dikkat etmek gerekir.
Kaynak/Referans:
39,32 ÷ 9 İşlemi ve Ondalık Sayılarla Temel Dört İşlem Nasıl Yapılır?
Soru:
Yukarıdaki resimde yer alan işlemlerde (örneğin “15,4 + 15,6 = 31,0” veya “28,20 - 11,20 = 17,0”) son satırda “39,32 ÷ 9 = ?” ifadesi bulunuyor. Bu bölme işlemi ondalık sayılarla yapılacaktır. Peki ondalık sayılarla bölme işlemi nasıl adım adım gerçekleştirilir ve bu işlemin sonucu nedir?
Cevap:
Aşağıda, hem soruda belirtilen işlemlerin mantığını hem de özellikle “39,32 ÷ 9” bölme işlemini nasıl yapacağınızı ayrıntılı örneklerle, tablolarla ve açıklamalarla anlatıyoruz. Ayrıca ondalık sayılarla toplama, çıkarma ve bölme gibi temel matematik işlemlerine dair bir rehber de sunuyoruz. Bu sayede benzer problemlerde nelere dikkat edilmesi gerektiğini de öğrenebilirsiniz.
İçindekiler
- Ondalık Sayılara Genel Bakış
- Ondalık Sayılarla Toplama
- Ondalık Sayılarla Çıkarma
- Ondalık Sayılarla Bölme
- Soruya Uygulama: 39,32 ÷ 9 İşlemi
- Benzer Örnekler ve Sık Yapılan Hatalar
- Özet Tablo: Ondalık Sayılarla Temel Dört İşlem
- Ek Bilgiler: Ondalık Sayılar Hakkında İpuçları
- Sonuç ve Özet
1. Ondalık Sayılara Genel Bakış
Ondalık sayılar, bir tam kısım ile bir ondalık (virgülden sonraki) kısımdan oluşur. Örneğin 15,4 sayısında:
- 15 tam kısmı,
- 4 ise ondalık kısım (virgülden sonraki ilk basamak).
Ondalık sayılar, günlük hayatta ölçümler (metre, kilogram vb.), para hesapları ve daha birçok yerde karşımıza çıkar. Matematikte ondalık sayılarla işlem yapabilmek, özellikle de dört temel işlem olan toplama, çıkarma, çarpma ve bölme konularında dikkatli olmak gerekir.
Bir ondalık sayı genellikle şu şekilde gösterilir:
Burada n, virgülden sonraki basamak sayısını ifade eder. Örneğin 15,4 sayısını
gibi düşünebiliriz.
2. Ondalık Sayılarla Toplama
Sorudaki ilk örneklerden biri “15,4 + 15,6 = 31,0” şeklindedir. Nasıl doğru sonuca ulaşıyoruz?
- Ondalık sayıları alt alta, virgülleri dik gelecek biçimde yazarız.
- Virgüller aynı sütunda olmalıdır.
- Gerekirse eksik basamakların yerine “0” koyarak toplama yaparız.
Örnek olarak:
| 1 | 5 | , | 4 | |
|---|---|---|---|---|
| + | 1 | 5 | , | |
| = | 3 | 1 | , | 0 |
Burada toplama yaparken, önce ondalık kısımları (4 + 6 = 10, elde 1), sonra tam kısımları (15 + 15 + elde 1 = 31) toplarız. İşlemi doğru yaptığımızda sonuç 31,0 olur.
3. Ondalık Sayılarla Çıkarma
Soruda verilen bir diğer örnek “28,20 - 11,20 = 17,0” şeklindedir. Neden sonuç 17,0?
- Yine virgülleri alt alta gelecek şekilde yazarız.
- İlk sayının ondalık kısmı 20 (yani 0,20), ikinci sayının ondalık kısmı da 0,20.
- Çıkarma yapıldığında 0,20 - 0,20 = 0,00 olarak hesaplanır ve tam kısma geçtiğimizde 28 - 11 = 17 elde edilir.
- Sonuçta 17,0 ya da kısaca 17 olarak yazılabilir.
Basit bir tabloyla gösterirsek:
| 2 | 8 | , | 2 | 0 | |
|---|---|---|---|---|---|
| – | 1 | 1 | , | 2 | 0 |
| = | 1 | 7 | , | 0 | 0 |
4. Ondalık Sayılarla Bölme
Ondalık bölme işleminde en önemli nokta, bölünen ve bölen sayıların virgüllerini dikkatle takip etmektir. Eğer bölen sayı ondalık ise bazen virgül kaydırma yöntemiyle böleni tam sayıya çevirmek ve aynı oranda bölünenin virgülünü de kaydırmak gerekir.
- Buradaki durumda bölen (9) bir tam sayıdır. Bu nedenle ek bir virgül kaydırma ihtiyacı yoktur.
- Bölünen sayı (39,32) ondalık bir değerdir. Adım adım klasik bölme algoritması uygulaması yaparız.
5. Soruya Uygulama: 39,32 ÷ 9 İşlemi
Soruda şu ifade yer almaktadır:
“39,32 ÷ 9 = ?”
Bu, ondalık bir sayının (39,32) tek basamaklı tam bir sayıya (9) bölünmesi sorusudur. Basamak basamak inceleyelim:
Adım 1: Tam Kısmı Bulma
Öncelikle 39’u 9’a bölerek başlarız.
- 9, 39’un içinde kaç defa vardır? 9 × 4 = 36’dır ve 9 × 5 = 45’tir; 45, 39’dan büyük olduğu için 39 içinde 9 en fazla 4 defa bulunur.
- Dolayısıyla 39 ÷ 9 = 4 (kalan 3).
Bu aşamada elde ettiğimiz tam kısım: 4.
Adım 2: Ondalık Kısımları İşleme Sokma
Kalan 3’ten sonra, virgülden sonraki kısma geçeriz. Sayımız 39,32 olduğu için virgülden sonra “32” basamağı vardır.
- Sırada, kalan (3) ile 3,2’yi (burada daha doğru ifade için 3’e ondalık basamak ekleyip “3,32” gibi düşünebiliriz) birleştirerek bölmeye devam ederiz.
Klasik bölme tablosu görünümü şu şekildedir (özet halde):
| 9 | ) | 39,32 |
|---|---|---|
| 4 | virgul ( . ) → | |
| – | 36 | |
| 3,32 |
Buradan sonra virgül kullanarak devam ederiz.
Adım 3: Gerekirse Virgülden Sonra Devam Etme
- 9’un 33’ün içinde kaç kez olduğunu araştırırız. Aslında burada 3,32 → 33,2 veya 33,20 gibi adımlar hesaplanabilir.
- 9, 33’ün içinde 3 defa (3×9 = 27) bulunur, kalan 6’dır.
- Kalan 6’yı sonraki basamak olan “2” ile birleştirince 62 oluşur. 9, 62’nin içinde 6 defa (6×9 = 54) bulunur, kalan 8’dir.
Eğer daha fazla basamak eklersek (örneğin 0 koyarak 80e dönüştürürsek) 9, 80’in içinde 8 defa (8×9 = 72) bulunur, kalan 8 olur ve süreç tekrarlamaya devam eder. Bu da büyük olasılıkla bir devreden ondalık elde edeceğiz anlamına gelir. Dolayısıyla tam olarak bölünmüyorsa ondalık basamaklar uzar veya tekrarlar.
Adım 4: Yaklaşık Değer
Pratik amaçlarla genelde 2 ondalık basamağa kadar veya istenen hassasiyette yuvarlama yapılır.
- 39,32 ÷ 9 ≈ 4,368…
- İki basamaklı yuvarlamayla \approx 4,37.
Dolayısıyla tam hassasiyetle yapmak istersek 4,368888… gibi uzayan bir sonuca ulaşabiliriz. Günlük yaşamda sık kullanılan yöntem, bu sayıyı 4,37 (iki ondalık basamakla) olarak almak şeklindedir.
6. Benzer Örnekler ve Sık Yapılan Hatalar
- Ondalık Kısmını Unutmak: Bazı öğrenciler bölme yaparken tam kısmı bulduktan sonra ondalık kısma geçmeyi unuturlar ya da hatalı şekilde eklerler.
- Virgülün Kaydırılmasını Karıştırmak: Eğer bölen de ondalık olsaydı (örneğin 3,1 gibi), önce onu tam sayıya çevirmek için virgül kaydırma işlemleri uygulamak gerektiğini unutmamak gerekir.
- Yuvarlama Kurallarını Göz Ardı Etme: Özellikle sonucun raporlanması sırasında 4,368…’i 4,37 yerine 4,36 diye hatalı yuvarlamak sık karşılaşılan bir hatadır.
Örnek:
- 12,6 ÷ 0,3 işleminde, önce 0,3’ün virgülünü sağa kaydırarak 3’e dönüştürülür, 12,6’nın virgülü de aynı oranda kaydırılarak 126 olur. Sonra 126 ÷ 3 = 42 sonucu elde edilir. Bu yöntemi çoğu kişi atlayarak hatalı sonuca gidebilir.
7. Özet Tablo: Ondalık Sayılarla Temel Dört İşlem
| İşlem | Örnek | Adımlar | Sonuç |
|---|---|---|---|
| Toplama | 15,4 + 15,6 | 1. Virgülleri alt alta yaz. 2. Ondalık kısımları topla. 3. Tam kısımları topla. 4. Elde varsa ekle. 5. Virgülü yerleştir. |
31,0 |
| Çıkarma | 28,20 – 11,20 | 1. Virgülleri alt alta yaz. 2. Ondalık kısımları çıkar. 3. Tam kısımları çıkar. 4. Sonucu (varsa) ondalık doğru yerde yaz. |
17,0 |
| Çarpma | 2,4 × 3,5 | 1. Ondalıkları yok sayarak çarp (24 × 35 = 840). 2. Sonuçtaki basamak sayısını toplamak için virgül kaydır (toplam 2 ondalık basamak = 8,40). |
8,40 |
| Bölme | 39,32 ÷ 9 | 1. Tam kısım bölmesini yap (39 ÷ 9 = 4, kalan 3). 2. Ondalık kısma geç (3,32 ÷ 9). 3. Bölme algoritmasına devam et. 4. Gerekirse yuvarla. |
≈ 4,37 (iki basamak) |
Bu tabloda gösterildiği gibi, bölme işlemi diğerlerine göre biraz daha detaylıdır. Ancak temel mantık, bölme algoritmasında kalanı bulduktan sonra virgülün sağındaki basamakları tek tek işleme sokmaktır.
8. Ek Bilgiler: Ondalık Sayılar Hakkında İpuçları
-
Doğru Yuvarlama:
- Çoğu zaman sonuçlar iki ondalık basamağa yuvarlanır (örn. “4,368…” → “4,37”).
- Eğer üçüncü basamak 5 veya daha büyükse, ikinci basamağı 1 artırarak yuvarlama yaparız.
-
İşlem Sırasında Kontrol:
- Hızlı bir kontrol için tahmini bir işlem yapılabilir. Örneğin 39 ÷ 9’un yaklaşık 4 civarı bir sayı vermesi gerektiğini biliyoruz. 39,32 biraz daha büyük olduğu için sonuç 4,3–4,4 civarında olmalı.
- Bu tahmin, sonucu bambaşka bir değerde (örneğin 13 gibi) bulma hatasını önler.
-
Bol Pratik Yapma:
- Ondalık sayılarla işlem yapmada en iyi yöntem çokça soru çözmektir.
- Toplama, çıkarma, çarpma ve bölme konularında farklı senaryolarla denk geldikçe eliniz alışır.
-
Parasalcı Örnekler:
- Yabancı para birimlerine çeviri veya banka hesaplarındaki kuruş/cent işlemleri genellikle ondalıklarla yürütülür. Bu da gerçek hayatta örnek alıştırma yapmaya fırsat sunar.
9. Sonuç ve Özet
- 15,4 + 15,6 = 31,0: Ondalık sayılarla toplama yapıldığında virgüller alt alta geldiğinde kolayca çözümlenir.
- 28,20 – 11,20 = 17,0: Ondalık sayılarla çıkarma da aynı mantıktadır. Ondalık kısımları ve tam kısımları ayrı değerlendirip yeniden birleştiririz.
- 39,32 ÷ 9: Bu bölme, klasik bölme algoritmasına göre ilerler. Tam kısım (39 ÷ 9 = 4) bulunduktan sonra kalanın virgüllü kısımla birleştirilmesi gerekir. Detaylı işlem sonunda 4,3688… gibi bir sonuç çıkar. İki basamaklı yuvarlamada sonuç 4,37 olarak alınabilir.
Böylece sorudaki tüm adımların mantığını anlamış oluyoruz:
- Toplama işlemleri (örnek: 15,4 + 15,6) ondalık kısımların dikkatli toplanmasıyla yapılır.
- Çıkarma işlemlerinde (örnek: 28,20 – 11,20) benzer şekilde ondalıklar eşit olmalı ve alt alta yerleştirilmelidir.
- Bölme işlemi (örnek: 39,32 ÷ 9) daha fazla adıma sahip olsa da mantığı, “tam kısım + ondalık kısım” şeklindeki klasik bölme rutinine dayanır.
Özetle, 39,32 ÷ 9 işleminin detaylı incelenmesi sonucunda:
- Kesin ve uzun ondalıklı değer: 4,368888… (tekrarlı ondalık).
- Yuvarlanmış (iki ondalık basamak): 4,37.
Bu tür sorularda, öğretmeninizin veya kitabın istediği tamlık derecesine (örneğin iki ondalık basamak, üç ondalık basamak vb.) göre son cevabı yazabilirsiniz.
Kaynaklar:
- MEB Ortaokul Matematik Ders Kitapları (Son Müfredat).
- OpenStax, “Elementary Algebra” (2021).