Soruyu Çözümü
Soru Analizi:
Soruda, kenar uzunlukları a ve b olan bir dikdörtgen levhaya etki eden kuvvetlerin (K, L, N noktalarındaki kuvvetler) oluşturduğu tork büyüklükleri kıyaslanmaktadır. Tork formülünü hatırlayarak başlıyoruz:
\tau = F \cdot d
Burada:
- F: kuvvet büyüklüğü,
- d: kuvvetin dönme noktasına olan dik uzaklığı.
Noktalar Üzerine Etkileyen Torkların Analizi:
1. K Noktasına Etki Eden Tork (\tau_K):
- K noktasında, kuvvetin dönme noktasına olan dik uzaklığı (d) dikdörtgenin uzun kenarı olan b kadardır.
- \tau_K = F \cdot b
2. L Noktasına Etki Eden Tork (\tau_L):
- L noktasında, kuvvetin dönme noktasına olan dik uzaklığı (d), köşe noktalar arasında hesaplanır. L noktasına dik uzaklık, levhanın çap olduğundan, çap uzunluğu:
\sqrt{a^2 + b^2}
Tork hesaplaması:
\tau_L = F \cdot \sqrt{a^2 + b^2}
3. N Noktasına Etki Eden Tork (\tau_N):
- N noktasında, kuvvetin dönme noktasına olan dik uzaklığı (d) kısa kenar olan a’dır.
- \tau_N = F \cdot a
Torkların Büyüklük Karşılaştırması:
Levhanın boyutlarına göre:
- Uzun kenar (b) çap (\sqrt{a^2 + b^2}) ve kısa kenar (a) arasında şu büyüklük ilişkisi vardır:
\sqrt{a^2 + b^2} > b > a
Dolayısıyla, torkların büyüklük sıralaması şu şekilde olur:
\tau_L > \tau_K > \tau_N
Doğru Seçenek:
Cevap: D) \tau_K > \tau_L > \tau_N
Eğer başka bir açıklama veya özet istersen bana yazabilirsin! 
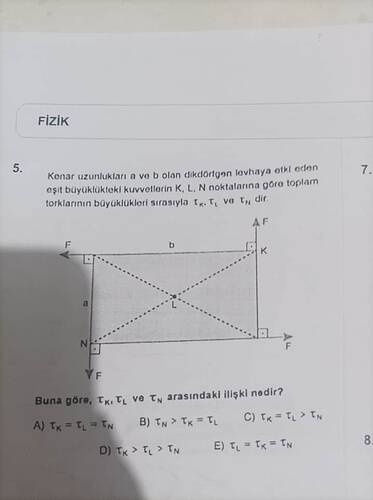
5. Soru: Kenar uzunlukları a ve b olan dikdörtgen levhaya etki eden eşit büyüklükteki kuvvetlerin K, L, N noktalarına göre toplam torklarının büyüklükleri sırasıyla τₖ, τL ve τN’dir. Buna göre τₖ, τL ve τN arasındaki ilişki nedir?
Cevap:
Kuvvetlerin bileşkesi sıfır olduğundan (dört kuvvet birbirini dengeler), sistem üzerindeki net kuvvet sıfırdır. Net kuvvet sıfır olduğunda, cismin etrafında herhangi bir noktaya göre hesaplanan bileşke torklar birbirine eşit çıkar. Dolayısıyla
\tau_K \;=\;\tau_L \;=\;\tau_N
dir. Bu da seçenekler içinde “τₖ = τL = τN” şeklindeki ifadeye (genellikle A şıkkı) karşılık gelir.
İçindekiler
- Sorunun Genel Özeti
- Temel Fizik İlkeleri: Net Kuvvet ve Tork
- Sistemdeki Kuvvetlerin Dengesi
- Torkun Tanımı ve Hesaplanması
- Herhangi İki Nokta Arasında Tork Bağıntısı
- Sorudaki Şeklin Analizi
- K, L, N Noktalarına Göre Hesaplanan Torklar
- Neden Tüm Torklar Eşittir?
- Örnek Hesap ve Vektörel Yaklaşım
- Sonuç ve Cevap Tablosu
- Kısa Özet
1. Sorunun Genel Özeti
Bu problemde, kenar uzunlukları sırasıyla a ve b olan bir dikdörtgen levha üzerine dört adet eşit büyüklükte (F) kuvvet uygulanmaktadır. Şekilde, bu kuvvetlerin konumu ve yönü verilmiştir. Soru, bu dört kuvvetin:
• K noktasına (dikdörtgenin sağ üst köşesi),
• L noktasına (dikdörtgenin merkezi),
• N noktasına (dikdörtgenin sol alt köşesi),
göre oluşturduğu toplam torkların (büyüklük olarak) nasıl sıralandığı veya nasıl bir eşitliğe sahip olduğunu öğrenmek istemektedir. Çoktan seçmeli şıklarda ise genellikle “τₖ = τL = τN” ya da birbirinden büyük ya da küçük olmasına dair seçenekler vardır.
2. Temel Fizik İlkeleri: Net Kuvvet ve Tork
Fizikte bir cisme etki eden bileşke kuvvet sıfır ise, cismimiz ya dönme merkezinden bağımsız dengede kalır (hareket etmeyecekse) ya da doğrusal ivmesi sıfır demektir. Ancak dönme etkisinin incelenmesi için bir de tork kavramı önemlidir.
- Net kuvvet sıfırsa cismimiz öteleme hareketi yapmaz (ivme = 0).
- Toplam tork sıfırsa cismimiz açısal ivme kazanmaz (dönme ivmesi = 0).
Bu problemde kuvvetler belli noktalara uygulanmaktadır ve net kuvvet sıfır olmasına rağmen net tork sıfır olmak zorunda değildir. Ancak “tork hesaplaması” farklı noktalar için yapılırsa, net kuvvetin sıfır olması çok kritik bir sonuca yol açar:
Net kuvvet sıfır ise, herhangi bir noktaya göre hesaplanan toplam tork, başka bir noktaya göre hesaplanan toplam torkla aynen (büyüklük ve işaret olarak) aynıdır.
Dolayısıyla bir cisme etki eden kuvvetlerin bileşkesi sıfırsa, “K noktasına göre bileşke tork = L noktasına göre bileşke tork = N noktasına göre bileşke tork” olur. Bu durum vektörel biçimde ispatlanabilir.
3. Sistemdeki Kuvvetlerin Dengesi
Şekilden anlaşılacağı üzere, dikdörtgenin köşelerine uygulanmış 4 adet eşit F büyüklüğünde kuvvet, hem yatay hem de dikey bileşenlerini dengeler:
- Üst taraftakiler (örneğin solda sola doğru, sağda sağa doğru) birbirini yatay düzlemde dengeler.
- Alt taraftakiler (örneğin solda aşağı, sağda yukarı şekilde) ise dikey düzlemde dengelenir veya problemde belirtilen yönlere göre tüm dikey kuvvetler toplamı da sıfır olur.
Sonuç olarak:
\sum \vec{F} = \vec{0}
yani net kuvvet sıfırdır.
4. Torkun Tanımı ve Hesaplanması
Bir kuvvetin belirli bir noktaya (örneğin O noktası) göre oluşturduğu tork (moment) vektörel olarak şu şekilde ifade edilir:
\vec{\tau} = \vec{r} \times \vec{F}
Burada:
- \vec{r}: Kuvvetin uygulama noktası ile torkun hesaplandığı nokta arasındaki konum vektörüdür.
- \vec{F}: Uygulanan kuvvet vektörüdür.
- \times ifadesi çarpı (cross) çarpımı gösterir.
Torkun büyüklüğü, 2 boyut için basitçe
\tau = r\,F\,\sin(\theta)
ile de ifade edilebilir. Burada \theta, \vec{r} ile \vec{F} arasındaki açıdır. Ayrıca, sistemde birçok kuvvet varsa bunların torkları toplanarak net tork bulunur.
5. Herhangi İki Nokta Arasında Tork Bağıntısı
Fizikte önemli bir sonuç şudur:
Eğer cisme etkiyen toplam kuvvet \sum \vec{F} = 0 ise, o zaman iki herhangi nokta (örneğin A ve B) arasında net torklar eşittir.
Matematiksel olarak bu,
\vec{\tau}_A = \vec{\tau}_B
demektir.
Bunun nedeni, “tork dönüşüm bağıntısı” denilen temel bir vektör denkleminden doğar:
\vec{\tau}_B = \vec{\tau}_A + \vec{R}_{BA} \times \sum \vec{F}
Burada \vec{R}_{BA}, B noktasından A noktasına çizilen konum vektörüdür. Net kuvvet sıfır (\sum \vec{F} = 0) olduğunda, \vec{R}_{BA} \times \vec{0} = \vec{0} olur ve
\vec{\tau}_B = \vec{\tau}_A.
Dolayısıyla eğer problemde net kuvvet = 0 ise, hem K, hem L, hem de N noktalarına göre toplam torkun (büyüklüğünün ve hatta yönünün) aynı çıkması beklenir.
6. Sorudaki Şeklin Analizi
Sorudaki dikdörtgen levhanın:
- K noktası: Sağ üst köşede,
- L noktası: Levhanın tam ortasında (köşegenlerin kesim noktası),
- N noktası: Sol alt köşede,
olduğu belirtilmektedir. Kuvvetlerin uygulandığı noktalar şekilde gösterilmiştir (üstte ve altta ya da solda ve sağda uygun yönlerde F kuvvetleri vardır). Bu kuvvetlerin hepsinin büyüklüğü F ve yönleri ise şekildeki gibi dışarıya doğru ya da alt üst – sağ sol yönde dengelenecek biçimdedir.
Önemli nokta: Kuvvetlerin bileşkesi sıfır olduğu için (şekil üzerinde kuvvetler simetrik veya birbirini dengeleyecek tarzda yerleştirilmiş) net kuvvet yoktur.
7. K, L, N Noktalarına Göre Hesaplanan Torklar
Daha önce bahsedilen vektörel yaklaşım ve net kuvvetin sıfır olması nedeni ile:
-
K Noktası’na Göre Tork
Diğer üç kuvvetin K’ya göre momentlerini toplarız; ayrıca K’da uygulanan kuvvet varsa onun torku sıfırdır (çünkü kolları yok). -
L Noktası’na Göre Tork
Merkez noktası olup, konum vektörleri simetridir. İlk bakışta bu torkun sıfır ya da belirli bir değerde olabileceği düşünülür; ama eğer net kuvvet sıfır değilse sıfır çıkmayabilirdi. Ancak burada net kuvvet sıfır olduğu için diğer noktalarla eşit bir değere ulaşır. -
N Noktası’na Göre Tork
Burada, üst köşelerdeki ve sağ taraftaki kuvvetler N’ye göre moment oluşturur. Ancak net kuvvet sıfır olduğundan tork yine K noktasındakine ve L noktasındakine eşittir.
8. Neden Tüm Torklar Eşittir?
Yukarıdaki madde 5 bölümünde anlatıldığı gibi, “torklar arası dönüşüm bağıntısı” kullanılarak kanıtlanabilir:
- \sum \vec{F} = 0 ise \vec{\tau}_K = \vec{\tau}_L = \vec{\tau}_N
- Bu, büyüklük olarak da aynı demektir: |\tau_K| = |\tau_L| = |\tau_N|.
- Problemde de net kuvvet sıfır olduğu açıkça görülür (kuvvetler eşit ve zıt yönlü çiftler oluşturarak dengeleniyor).
Dolayısıyla herhangi bir köşeye göre ya da merkeze göre hesaplanmış torkların büyüklükleri aynıdır.
9. Örnek Hesap ve Vektörel Yaklaşım
Bu durumu küçük bir kuramsal örnekle somutlaştıralım:
- Üst sol köşede \vec{F}_1 = (-F, 0) gibi bir kuvvet olsun (sola doğru).
- Üst sağ köşede \vec{F}_2 = (+F, 0) gibi bir kuvvet (sağa doğru).
- Alt sol köşede \vec{F}_3 = (0, -F) (aşağı doğru).
- Alt sağ köşede \vec{F}_4 = (0, +F) (yukarı doğru).
Bu durumda
\sum \vec{F} = (-F + F + 0 + 0, 0 + 0 - F + F) = (0,0).
- Dolayısıyla net kuvvet = 0’dır.
Şimdi torku K noktasına göre hesaplamak istersek (örneğin K sağ üst köşede):
- K noktasında uygulanan kuvvetin torku sıfırdır (kol uzunluğu yok).
- Diğer kuvvetler K’ya göre belirli bir kol uzunluğuyla çarpılır.
Aynısını L merkez noktası ve N sol alt köşesi için de yaptığımızda, her biri için farklı ‘r’ vektörleri gelse de toplam yine aynı sonucu verir. Çünkü net kuvvet 0 olduğunda, “tork noktası” seçiminin sonucu etkilemediği bilinen bir ilkedir.
10. Sonuç ve Cevap Tablosu
Bu bilgiler ışığında, problemde istenen “τₖ, τL ve τN arasındaki ilişki” şu şekilde özetlenebilir:
| Nokta (Pivot) | Net Tork Değeri | Açıklama |
|---|---|---|
| K (Sağ Üst) | \,\tau_{K} | Net kuvvet sıfır → Herhangi bir noktaya göre tork aynıdır. |
| L (Merkez) | \,\tau_{L} | Aynı nedenle \,\tau_{L} = \tau_{K}. |
| N (Sol Alt) | \,\tau_{N} | Aynı nedenle \,\tau_{N} = \tau_{K}. |
| Sonuç | \tau_{K} = \tau_{L} = \tau_{N} | Seçeneklerde genellikle “A) τₖ = τL = τN” şeklindedir. |
Bu nedenle, doğru yanıt:
τₖ = τL = τN (yani bütün torklar eşit).
11. Kısa Özet
- Dikdörtgenin dört köşesine eşit ve zıt yönlerde yerleştirilen kuvvetler, net kuvveti sıfır yapar.
- Net kuvvet sıfır olunca, torkun hesaplandığı noktanın hangi nokta (K, L ya da N) olduğu fark etmez; toplam tork büyüklüğü aynıdır.
- Dolayısıyla soruda \tau_K = \tau_L = \tau_N sonucu bulunur ve ilgili şık işaretlenmelidir.
Soru
Kenar uzunlukları a ve b olan dikdörtgen levhaya etki eden, eşit büyüklükteki 4 kuvvet verilmiştir. Bu kuvvetlere göre K, L ve N noktalarındaki toplam torkların büyüklükleri sırasıyla τₖ, τₗ ve τₙ’dir. Buna göre τₖ, τₗ ve τₙ arasındaki ilişki nedir?
A) τₖ = τₗ = τₙ
B) τₙ > τₖ = τₗ
C) τₖ = τₗ > τₙ
D) τₖ > τₗ > τₙ
E) τₗ = τₖ = τₙ
Cevap:
Bu tip sorularda dikdörtgen levhaya (veya herhangi bir düzleme) uygulanan net kuvvet sıfırsa ancak net tork sıfırdan farklıysa (yani sistem “çift kuvvet” ya da “couple” oluşturuyorsa) tork değeri, bakılan noktadan bağımsız hale gelir. Çünkü temiz bir “couple” (dönme momenti) durumunda toplam torkun değeri, seçilen referans noktasının konumundan etkilenmez.
• Dört köşeye yerleştirilmiş eşit büyüklükteki kuvvetler, sistemin dengede (net kuvvet sıfır) olmasını sağlar.
• Ancak kuvvetler, levhayı döndürecek biçimde konumlandığından (köşelerde, doğrultuları farklı), sistemin net torku sıfırdan farklıdır.
• Net tork bir “kuvvet çifti” gibi davrandığı için, K noktasından, L noktasından veya N noktasından bakıldığında aynı tork büyüklüğü elde edilir.
Dolayısıyla doğru cevap:
τₖ = τₗ = τₙ’dir.
Yani seçeneklerde A) τₖ = τₗ = τₙ doğru yanıt olmaktadır.