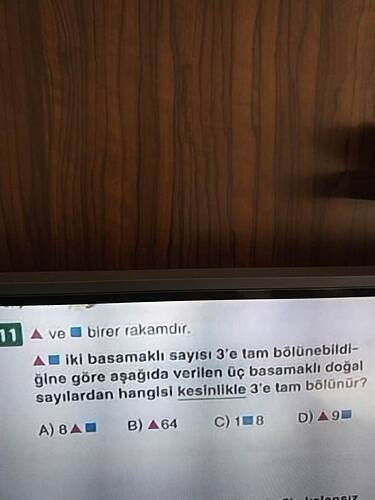
İki basamaklı bir sayı 3’e tam bölünebiliyorsa, aşağıda verilen üç basamaklı doğal sayılardan hangisi kesinlikle 3’e tam bölünür?
Bir sayının 3’e tam bölünebilmesi için rakamlarının toplamının da 3’e bölünebilir olması gerekir.
İlk olarak, iki basamaklı sayımızı ele alalım:
- İki basamaklı sayımızın rakamları: \triangle ve \square.
- \triangle + \square sayısı 3’e bölünebilir.
Verilen seçenekler:
A) 8$\triangle$
B) $\triangle$64
C) 18$\square$
D) 9$\triangle\square$
Şimdi her bir seçeneği değerlendirelim:
-
A) 8$\triangle$:
Rakamlarının toplamı 8 + \triangle. Eğer \triangle + \square sayısı 3’e bölünüyorsa, \triangle yerine herhangi bir rakam yazılabilir. Ancak kesin bir şekilde bu toplamın 3’e bölünüp bölünmeyeceğini söyleyemeyiz. -
B) $\triangle$64:
Rakamlarının toplamı \triangle + 6 + 4 = \triangle + 10. Eğer bu toplamın her zaman 3’e bölüneceğini kanıtlayamıyorsak, kesin bir sonuç sağlayamayız. -
C) 18$\square$:
Rakamlarının toplamı 1 + 8 + \square = 9 + \square. 9 zaten 3’e bölünebilir bir sayıdır, $\square + \triangle$’ın da 3’e bölünebildiğini biliyoruz. Böylece bu seçenekte toplam her durumda 3’e bölünebilir. -
D) 9$\triangle\square$:
Rakam toplamı 9 + \triangle + \square olur. Ancak 9 zaten 3’e bölünebiliyor ve \triangle + \square da 3’e bölünebiliyor, dolayısıyla bu da bir aday olabilir. Ancak \triangle + \square sayısının kesinliği açısından C seçeneği daha garanti bir seçenektir çünkü verilen bilgi doğrudan kullanılmıştır.
Sonuç: C seçeneği, yani 18$\square$ sayısı kesinlikle 3’e tam bölünür çünkü 9 ve \square toplamı daima 3’e bölünebilen bir ifade verir.