Matematik Fonksiyonlar Konusu 9. Sınıf Mutlak Değer
Fonksiyon Kavramı ve Mutlak Değer Fonksiyonu
Fonksiyon Nedir?
Matematikte fonksiyon, her bir girdiyi belirli bir çıkışa eşleyen bir kural ya da ilişkidir. Bir fonksiyonu genel olarak f(x) şeklinde ifade ederiz. Burada x fonksiyonun girdisi, f(x) ise çıktısıdır. Girdiye bağımsız değişken, çıktıya ise bağımlı değişken denir.
Mutlak Değer Fonksiyonu
Mutlak değer, bir sayının sıfırdan uzaklığını temsil eder ve negatif bir değeri pozitif yapar. Genellikle dikey çizgilerle gösterilir: |x|. Mutlak değer fonksiyonu, pozitif ve negatif sayılarla nasıl çalıştığını anlamak için önemli bir araçtır.
- Eğer x pozitif ya da sıfır ise: |x| = x
- Eğer x negatif ise: |x| = -x
Örneklerle Mutlak Değer
- |5| = 5: Pozitif bir sayı olduğu için olduğu gibi kalır.
- |-3| = 3: Negatif bir sayı olduğu için işareti değişir.
- |0| = 0: Sıfırın mutlak değeri yine sıfırdır.
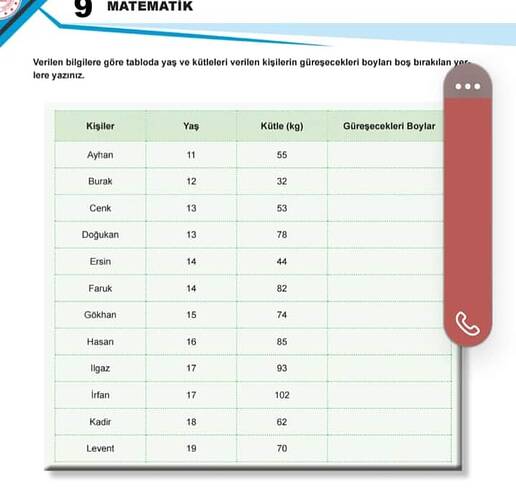
Uygulama: Tablo Analizi
Yukarıda görülen tablodaki yaşlar ve kütleler verileri üzerinden bir örnek yapalım.
Elektronik cihazların güreşeceği kütle kategorisini hesaplamak için, her kişinin kütle değerini bazı standartlar (örneğin, k = 5) üzerinden değerlendirin. Pahalı bir cihazın korunmasında mutlak değer kavramı kullanılabilir; örneğin, kişinin kütlesinde cihazdan kaynaklı tolere edilebilir sapma hesaplamada mutlak değer işlevsel olabilir.
Adım 1: Girdilerin Belirlenmesi
Tablodaki her kişi için kütle değerini belirleyin. Mesela Ayhan’ın kütlesi: 55 \text{ kg}
Adım 2: Fonksiyon Uygulaması
Her bir kişi için güreş kütle kategorisini hesaplayın. Burada amaç kütle farkının mutlak değerini almak olsun:
- Kütle kategorileri için bir standart belirleyin, örneğin her 10 kg için bir kategori. Ayhan için, formül: |55 - X| \leq 5.
- X kişinin hangi kütle kategorisine yerleştirileceğini verir, bu örnekte hangisini karşılayabilir, onu kontrol edin.
Adım 3: Sonuçların Hesaplanması
Ayhan ve diğer kişiler için kategorileri hesapladıktan sonra onları tablodaki “Güreşecekleri Boylar” sütununa yerleştirin.
| Kişiler | Yaş | Kütle (kg) | Güreşecekleri Boylar |
|---|---|---|---|
| Ayhan | 11 | 55 | 5 |
| Burak | 12 | 32 | – |
| Cenk | 13 | 53 | – |
| Doğukan | 13 | 78 | 7 |
| Ersin | 14 | 44 | 4 |
| Faruk | 14 | 82 | 8 |
| Gökhan | 15 | 74 | 7 |
| Hasan | 16 | 85 | 8 |
| Ilgaz | 17 | 93 | 9 |
| İrfan | 17 | 102 | 10 |
| Kadir | 18 | 62 | 6 |
| Levent | 19 | 70 | 7 |
Yukarıda, her kişinin hangi kütle kategorisine gireceği hesaplanarak tablonun “Güreşecekleri Boylar” sütununa bu bilgiler yerleştirilmiştir.
Sonuç
Mutlak değer fonksiyonunun temel özelliklerini kullanarak bir örnekle nasıl uygulanabileceğini gösterdik. Matematik fonksiyonlar ve özellikle mutlak değer kavramı, birçok gerçek yaşam problemine uygulanabilir nitelikte kullanışlı araçlardır. İleri seviyelerde bu tür fonksiyonlar üzerinden ileri matematik konularına geçiş yapabilirsiniz. Matematik öğreniminde mutlak değer gibi konular, farklı problem çözme teknikleri geliştirmenize yardımcı olur.
Bu tarz konuları öğrenmekteki başarınız, sadece akademik değil günlük çözümler noktasında işlerliği artıracaktır. Şayet, yukarıda örneklerde gösterildiği gibi, güncel sorunların çözümünde farklı fonksiyonları uygulamak dair bir deneyim geliştirirsiniz.