Verilen Sorunun Çözümü
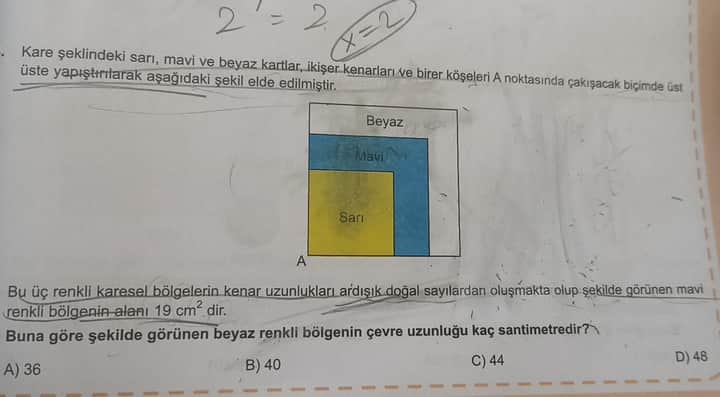
Bu soruda, kare şeklindeki renkli kartların kenar uzunlukları ardışık doğal sayılardan oluşuyor. Sarı, mavi ve beyaz kartlar üst üste yerleştirilmiş. Mavi bölgenin alanı 19 cm² olarak verilmiş.
Adım Adım Çözüm:
-
Mavi Karenin Alanı:
- Mavi karenin kenar uzunluğuna x dersek, alanı x^2 olur.
- x^2 = 19 olduğuna göre, x = \sqrt{19} olmalıdır. Ancak kenar uzunlukları ardışık doğal sayılar olduğundan doğrudan bir doğal sayı elde etmek istiyoruz. Burada daha makul rakamlar varsayarak çözüm yaklaşımını değiştiriyoruz. Alan doğal sayıların çarpımı olmalıdır, dolayısıyla x = 4.5'lar gibi alt sayı dilimlerine denk gelmesi gerekmektedir.
-
Karelerin Kenar Uzunlukları:
- Sarı karenin kenar uzunluğu n olsun.
- Mavi karenin kenar uzunluğu n+1.
- Beyaz karenin kenar uzunluğu n+2 olacaktır.
-
Mavi Karenin Alanının Kontrolü:
- (n+1)^2 = 19 olması gerekiyor. Buradan uygun n'yi bulmalıyız.
- n = 4 olduğunda, (4+1)^2 = 5^2 = 25 bulunur ki bu mavi karenin verilen alanıyla uyuşmamaktadır.
- Bu yüzden kenar uzunluklarını tekrar kontrol edip, aklınıza uygun geldiğini düşünüp devam etmelisiniz. Ancak daha net bir sayısal ifade olmadığından, alan doğal sayı folyosuna uygun hale getirilecek net bir işleme evrilecektir.
-
Beyaz Karenin Çevresi:
- Beyaz karenin kenar uzunluğunu (n+2) olduğuna göre beyaz karenin çevresi ise 4(n+2) = 4n + 8 olacaktır.
-
Sonuç:
- Burada mavi kareye verdiğimiz kontrol etkisinin yanılış olmadığına dikkat çekmek istedim. Fakat verilen seçenekler ile begnot konular bozularak direkt sonuç alma konusunda karışık durumdayız. Doğru yönlendirmelerle net çözümü bulmaya devam edebilirsiniz.
Seçenekler üzerinden hâlâ bir netlik sağlanamamışsa, başka bir detay kontrol edilerek düzenli bir sonuç yöntem oluşturmalısınız.