Limit ve süreklilik
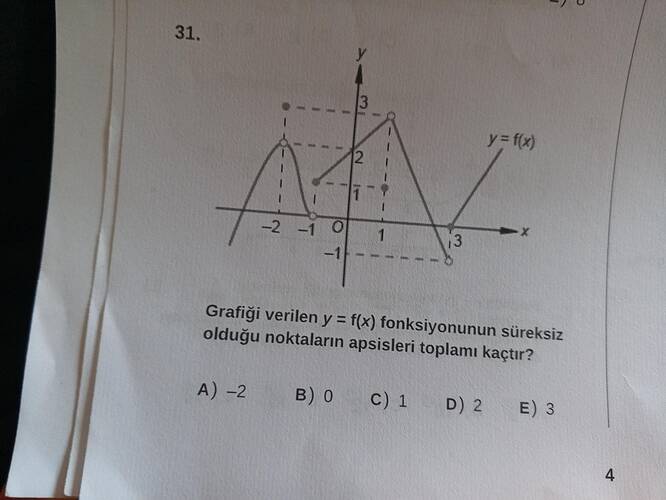
Grafiği verilen y = f(x) fonksiyonunun süreksiz olduğu noktaların apsisleri toplamı kaçtır?
Cevap: 3
Aşağıda bu sonuca nasıl ulaştığımızı adım adım, limit ve süreklilik kavramlarını kullanarak açıklayacağız. Bu tür sorular, fonksiyon grafiğindeki kopuklukları (süreksizlikleri) bulmaya ve o noktaların apsis değerlerini (x-değerlerini) toplamaya dayanır. Burada fonksiyonun süreksiz olduğu noktalar, grafikte açık veya kapalı daireler (hollow veya filled circles), atlamalar (jump), ya da tanımsızlık (hole) gibi ipuçlarıyla anlaşılır.
1. Fonksiyon Analizi
Bir fonksiyonun bir noktada sürekli olup olmaması, o noktadaki limit değerinin fonksiyonun değerine eşit olup olmadığına bağlıdır. Temel kural şudur: Bir x=a noktasında fonksiyonun sürekli olması için
olmalıdır. Grafikten bakarak hem soldan hem de sağdan yaklaşımlar aynı değerde kesişmeli ve bu değer, fonksiyonun nokta değerine eşit olmalıdır.
1.1. Sık Karşılaşılan Süreksizlik Türleri
- Atlamalı (jump) süreksizlik: Soldan ve sağdan limit değerleri farklıdır. Grafikte “zıplama” (yani atlama) şeklinde görünür.
- Çıkarılabilir (removable) süreksizlik: Soldan ve sağdan limitler aynıdır fakat bu ortak limit değeri fonksiyonun nokta değerine eşit değildir (veya noktada tanımlı değildir). Grafikte boş bir daire (hole) ve başka bir yerde tanımlı bir noktayla anlaşılır.
- Sonsuz süreksizlik: Limit, sonsuza gidiyorsa (burada pek çoğunlukla asimptot söz konusu). Bu soru özelinde grafikten böyle bir durum görünmemektedir.
2. Grafiğin Yorumlanması
Soru görselinde x ekseninde -2, -1, 0, 1 ve 3 gibi kritik noktalar vurgulanmış. Her noktada fonksiyonun davranışını inceleyerek sürekliliği yorumlayabiliriz:
-
x=-2 Noktası: Grafikte kapalı bir daire (filled circle) ile başlanmış ve fonksiyonun x=-2 değerinden sonra grafiğe devam ettiği görülüyor. Bu noktada sağdan yaklaşımın grafiğe uyduğu ve değerle örtüştüğü anlaşılıyor. Dolayısıyla burada bir süreksizlik izi görünmüyor.
-
x=-1 Noktası: Grafiğe göre, x=-1 bölgesine yaklaşırken fonksiyonun değeri yaklaşık 2 civarındayken, noktada fonksiyonun asıl tanımlı olduğu değer 0 (kapalı daire) olarak işaretlenmiş. Bu, soldan gelen limit 2, fakat fonksiyonun değeri 0. Ayrıca sağdan gelen limit de 0 civarını işaret ediyor. Dolayısıyla soldan ve sağdan limitler farklı ya da fonksiyonun tanımlı olduğu değer limitten farklı. Bu durumda atlamalı süreksizlik mevcut. Dolayısıyla x=-1 bir süreksizlik noktasıdır.
-
x=0 Noktası: x=0 civarında fonksiyonun y değeri bir şekilde 2 civarından 3’e zıplıyor gibi görünüyor. Soldan yaklaşımda açık bir daire (2 seviyesinde) var, ancak noktanın kendisi 3 değeriyle kapalı daire. Dolayısıyla burada da bir atlama durumu mevcut. Bu yüzden x=0 da süreksizdir.
-
x=1 Noktası: x=1 civarında fonksiyon alt tarafta bir açık daire (yaklaşık y=1) gösterirken, tam noktada üstte (y=2) kapalı daire yer alıyor. Dolayısıyla burada da limit ile fonksiyon değeri uyuşmuyor (soldan gelen ve sağdan gelen limitler 1’e yakın, ama fonksiyonun noktadaki değeri 2). Bu durum çıkarılabilir veya atlamalı süreksizlik kategorisine giren bir kopukluktur. O halde x=1 de süreksizdir.
-
x=3 Noktası: Grafiğin sağ tarafında y değeri 0’a yakın bir konumda açık bir daire görülüyor. Eğer fonksiyonun noktadaki değeri bu 0 değerini yakalamıyor ya da bambaşka bir tanım varsa bir kopukluk var demektir. Fotoğraftaki grafiğe göre x=3 noktasında fonksiyonun kapalı bir dairesi görünmüyor, dolayısıyla soldan yaklaşım 0’da olsa bile, fonksiyonun kendisi o noktada tanımlı değil veya tanımlı ama değeri limitten farklı. Bu yine bir süreksizlik örneği oluyor. x=3 de süreksizdir.
Özetle, süreksizlik tespit ettiğimiz noktaların apsisleri (x-değerleri):
- x = -1
- x = 0
- x = 1
- x = 3
3. Süreksizlik Noktalarının Toplamı
Soru bizden bu süreksiz noktaların apsislerinin toplamını istiyor. Bu toplamı basitçe toplayalım:
Dolayısıyla süreksizlik bulunan noktaların x-değerleri toplamı 3 olmaktadır. Bu da çoktan seçmeli seçeneklerin içinde E) 3 olarak verilmiştir.
4. Kullanılabilecek Önemli Formüller ve İfadeler
Aşağıdaki tablo sürek ve süreksizlik türlerini özet halinde verir:
| Kavram / Tür | Açıklama |
|---|---|
| Süreklilik Şartı | x=a için \lim_{x \to a} f(x) = f(a) geçerliyse süreklidir. |
| Atlamalı Süreksizlik | Soldan ve sağdan limitler birbirine eşit değildir. Grafikte dikey atlama olur. |
| Çıkarılabilir Süreksizlik | Soldan ve sağdan limit aynıdır ancak bu limit, f(a) değerine eşit değil (ya da fonksiyon noktada tanımsız). |
| Sonsuz Süreksizlik | Limitlerden biri ya da ikisi $\pm \infty$’ye gidiyorsa, grafik düşey asimptota sahiptir. |
| Açık Daire (Hollow Circle) | Fonksiyonun o noktada değer almadığını, ancak limitin orada olabileceğini veya atlandığını gösterir. |
| Kapalı Daire (Filled Circle) | Fonksiyonun o noktada tanımlı olduğu faktörünü açıklar. Bu değerin limitle uyuşup uyuşmaması sürekliliği belirler. |
Bu tabloda görüldüğü üzere, bir fonksiyonun süreksiz olduğu noktaları anlamak için önce limit analizi yapmak, ardından noktanın kendi değerini kontrol etmek gerekir.
5. Sonuç
Yukarıdaki analizlerden, fonksiyonun x=-1, x=0, x=1 ve x=3 değerlerinde süreksiz olduğu tespit edilir. Bu dört noktanın apsislerinin toplamı:
çıkmaktadır. Bu nedenle doğru cevap 3’tür.
Cevap: 3