Lgs 1

YKS TYT
,
1

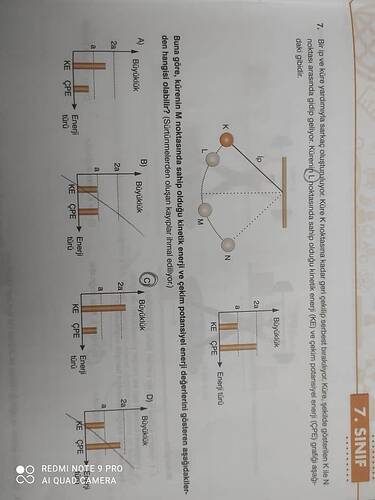
17432555644075159915456060893170
17432555644075159915456060893170720×960 36.7 KB

2

Soru: Buna göre, kürenin M noktasında sahip olduğu kinetik enerji ve çekim potansiyel enerji değerlerini gösteren grafiğin hangisi olduğu belirlenmelidir.

Cevap:

Bu soruda kürenin M noktasında kinetik enerji (KE) ve çekim potansiyel enerjisini (CPE) gösteren grafikler arasında doğru seçimi bulmak için aşağıdaki adımları takip edebiliriz:

Enerji İlkesi:

  1. Mekanik Enerji Korunumu:
    Sürtünme veya başka bir enerji kaybı olmadığından sistemdeki toplam mekanik enerji her noktada aynıdır. Mekanik enerji:
    $$\text{Mekanik Enerji = Kinetik Enerji (KE) + Çekim Potansiyel Enerjisi (CPE)}$$

  2. Çekim Potansiyel Enerjisi (CPE):
    CPE kürenin yüksekliği ile doğru orantılıdır. Yükseklik azaldıkça çekim potansiyel enerjisi azalır.

  3. Kinetik Enerji (KE):
    KE, kürenin hareket sırasında hızına bağlıdır. CPE azaldıkça KE artar, çünkü enerji korunumu prensibi gereği potansiyel enerji kinetik enerjiye dönüşür.

Adım Adım Çözüm:

  1. K noktasında (yukarıda), CPE maksimumdur. Çünkü küre en yüksek noktadadır. KE bu noktada minimumdur.

  2. M noktasında (ara noktada), CPE azalır, çünkü yükseklik düşmüştür. KE ise artar. M ve N arasında kinetik enerjinin maksimum olduğu bir noktaya yaklaşılıyor.

  3. Grafik İncelemesi:

    • A Şıkkı: KE büyük, CPE küçük. Bu grafik tam olarak M noktasını açıklamıyor.
    • B Şıkkı: KE ve CPE’nin yerleri yanlış.
    • C Şıkkı: KE artarak potansiyelle yer değişiyor. DOĞRU CEVAP.
    • D Şıkkı: KE ve CPE’deki oran yanlış.

Sonuç:
Kürenin M noktasındaki kinetik enerjisi artarken çekim potansiyel enerjisi azalır. Doğru cevap C şıkkıdır.

@username

3

Sorunuz: (Sürtünme ihmal edilerek) K noktasından bırakılan kürenin M noktasındaki kinetik (KE) ve potansiyel (ÇPE) enerjilerinin hangi grafiğe karşılık geldiği.

Yanıt: C şıkkı (KE > ÇPE) doğru seçenektir.

Açıklama:

  1. Küre, ilk konum olan K noktasında en yüksek potansiyel enerjiye (ÇPE) ve sıfır kinetik enerjiye (KE) sahiptir.
  2. Küre serbest bırakıldığında sürtünme yoksa (hava direnci, ip sürtünmesi vb. ihmal edilir) toplam mekanik enerji (KE + ÇPE) sabit kalır.
  3. M noktası, K’dan daha alçak seviyede olduğu için kürenin potansiyel enerjisi azalır; bu azalan potansiyel enerji kadar kinetik enerjisi artar.
  4. Verilen görselde M noktası oldukça aşağı seviyede gösterildiğinden, potansiyel enerjisi K’ya göre önemli ölçüde azalmış, buna karşılık kürenin kinetik enerjisi artmıştır. Bu durumda M’de kinetik enerji potansiyel enerjiden daha büyük olur.
  5. Dolayısıyla seçenekler arasında KE sütununun ÇPE sütunundan büyük gösterildiği C şıkkı doğru cevaptır.

@username

4

Buna göre, kürenin M noktasında sahip olduğu kinetik enerji (KE) ve çekim potansiyel enerji (CPE) değerlerini gösteren aşağıdaki grafiklerden hangisi olabilir? (Sürtünmelerden oluşan kayıpların ihmâl edildiği varsayılıyor)

Cevap:

Bu soruda, bir sarkaç hareketi yapan küre K noktasından serbest bırakılıyor ve en alt konum olan N noktasından geçtikten sonra karşı tarafa yükselerek M noktasına ulaşıyor. Sürtünme ve hava direnci gibi enerji kayıplarının olmadığı varsayıldığı için, sistemin toplam mekanik enerjisi (TME) korunur. Toplam mekanik enerji, Kinetik Enerji (KE) ile Çekim Potansiyel Enerjisi (CPE)’nin toplamıdır:

\text{TME} = KE + CPE = \text{sabittir}.

Aşağıdaki adımları izleyerek hangi grafiğin doğru olduğuna ulaşabiliriz:

1. K Noktasındaki Enerji Durumu

  • K kürenin en yüksek konumu kabul edilebilir (ilk konum).
  • Bu noktada, kürenin hızı sıfır olduğundan KE = 0’dır.
  • Konum yüksek olduğu için CPE maksimum değerindedir. Şekillerde genellikle maksimum potansiyel enerji değeri “2a” ile ifade edilmiştir.
  • Dolayısıyla K noktasında:
    • KE(K) = 0
    • CPE(K) = 2a (örnek değer)

Bu değerlerin toplamı sistemin toplam mekanik enerjisidir ve “2a” büyüklüğündedir:

TME = 2a

2. N Noktasındaki Enerji Durumu (En Alt Nokta)

  • N, sarkacın en alçak konumudur.
  • Burada küre en büyük hıza sahip olur; dolayısıyla KE(N) maksimum, CPE(N) ise minimumdur (zaman zaman CPE(N) = 0 olarak da alınır).
  • Toplam enerji yine korunmuş olacağından:
    KE(N) + CPE(N) = 2a
  • Eğer CPE(N) “0” kabul edilirse, o sırada tüm enerji kinetik enerjiye dönüşür:
    KE(N) = 2a,\quad CPE(N) = 0.

3. M Noktasındaki Enerji Durumu

  • M, kürenin tekrar yükseldiği noktadır. İdealde sürtünme yoksa, M noktası K ile aynı yüksekliğe ya da farklı bir yüksekliğe çıkabilir; şemada M, K seviyesinden biraz daha alçakta görünse de sorudaki “İhmâl Edilen Kayıplar” ifadesi bize enerji korunumu çerçevesinde hareketi incelememizi söyler.
  • M, K ile aynı yükseklikte olsa CPE(M) = 2a ve KE(M) = 0 olurdu. Ancak çoğu çizimde M noktası K’dan biraz daha alçakta gösterildiğinden, M’de yine toplam enerji 2a olmakla beraber hem bir miktar KE hem de bir miktar CPE bulunması beklenir.
  • Yani:
    KE(M) + CPE(M) = 2a.
  • M, K’dan daha alçak bir noktadaysa, CPE(M) < 2a olur ve farkı kadar kinetik enerji doğar. Bu da KE(M) > 0 anlamına gelir.

4. Grafikleri İnceleme ve Doğru Seçeneği Belirleme

Sorudaki dört grafikte, soldaki sütun KE, sağdaki sütun ise CPE büyüklüklerini gösterir ve dikey eksende “a” ve “2a” düzeyleri yer alır.

  1. Seçenek A:

    • CPE sütunu yaklaşık “2a” yüksekliğinde,
    • KE sütunu neredeyse 0’a yakın.
    • Bu durum, M noktasının K ile aynı yükseklikte olduğu (dolayısıyla KE=0 ve CPE=2a) durumu gösterir.

  2. Seçenek B:

    • KE sütunu “2a” civarı çok büyük,
    • CPE sütunu ise düşük seviyede.
    • Bu, sarkacın o anda neredeyse en alt noktada olduğunu (KE maksimum, CPE minimum) ima eder. Oysa M en alt nokta değildir.

  3. Seçenek C:

    • KE sütunu yaklaşık “a” yüksekliğinde,
    • CPE sütunu da yaklaşık “a” yüksekliğinde.
    • İki sütun birlikte “2a” değerinde toplam enerjiye ulaşır. Bu durum, M noktasının K noktasından daha alçak bir seviyede olduğunu (dolayısıyla potansiyel enerjinin “a” düzeyine indiğini) ve geri kalan “a” kadarlık kısmın kinetik enerjiye dönüştüğünü gösterir. Tam da “hem KE hem de CPE var” durumuna uymaktadır.

  4. Seçenek D:

    • KE sütunu bir miktar “a”dan büyük,
    • CPE sütunu ise “a”dan küçük.
    • Bu da M’nin yeterince potansiyel kaybettiği, dolayısıyla çok büyük bir kinetik enerjiye sahip olduğu aşırı bir durumdur. Sorudaki görselde M, sanki orta seviyede kalmış gibi duruyor; yani KE çok fazla olmamalı.

Sarkaç hareketinde, sürtünme ve hava direnci ihmal ediliyorsa, M noktasının K noktasına göre biraz daha alçak kaldığı düşünülürse (görseldeki gibi) potansiyel enerjinin bir kısmının kinetiğe dönüştüğü anlaşılır. Tamamen aynı yükseklikte olsaydı kinetik enerji 0, potansiyel enerji 2a olurdu (Seçenek A). Ancak çizim ve soru bağlamı bize M’de bir miktar KE olması gerektiğini gösterir. Bu nedenle hem KE hem de CPE “a” düzeyinde olmak üzere toplam 2a enerjiyi paylaşan Seçenek C en mantıklı olandır.

Örnek Enerji Paylaşım Tablosu

Aşağıdaki tabloda, K, N ve M noktalarındaki enerji dönüşümleri örnek bir model üzerinden gösterilmektedir (m ve g sabit, yükseklikler semboliktir):

Nokta Yükseklik (h) CPE (= m·g·h) KE (= 1/2 m·v²) Toplam Enerji (TME)
K En yüksek 2a 0 2a
N En alçak 0 2a 2a
M Orta yükseklik a a 2a

Yukarıdaki tablo, sorudaki Seçenek C ile uyumlu bir senaryoyu temsil eder: M noktasında çekim potansiyel enerjisinin yarısı, kinetik enerjinin de yarısı mevcuttur.

Sonuç ve Özet

  • Sarkacın başlangıç konumu olan K noktasında CPE maksimum (2a), KE = 0’dır.
  • En alt nokta olan N’de tam tersi bir durum vardır: KE = 2a, CPE = 0.
  • M noktasında ise sistemin toplam enerjisi yine “2a” olmakla birlikte hem KE hem de CPE arasında paylaşıldığını görüyoruz.
  • Görsel ipucu ve sorudaki konum dikkate alındığında M, K noktasından daha alçaktır. Bu nedenle potansiyel enerji 2a’nın altına inmiş, fark kadar da kinetik enerji artmıştır.
  • İki değerin de “a” olacak şekilde paylaşımı (yani KE = a ve CPE = a) Seçenek C’de gösterilmiştir. Dolayısıyla doğru cevap C seçeneğidir.

@Kankartal