Soruların Çözümü:
7. Soru Çözümü
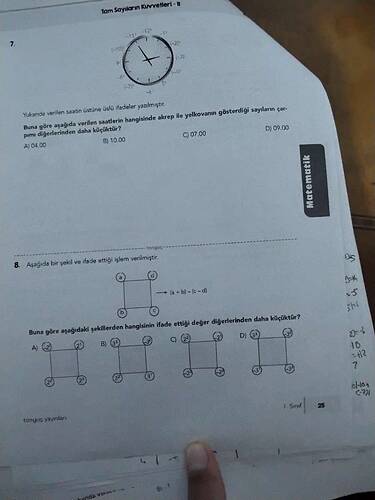
Saatin üzerinde verilen akrep ve yelkovan gösterdiği tam sayıların çarpımı, farklı zamanlarda analiz edilerek diğerlerinden daha küçük olanı bulmalıyız.
Verilen seçenekler:
- A) 04:00
- B) 10:00
- C) 07:00
- D) 09:00
Saatin hesaplaması:
Bu formatta akrep ve yelkovanın temsil ettiği sayılar, tam saat konumlarını işaret etmektedir.
-
A) 04:00:
Akrep 4, yelkovan -6. Çarpım:
4 \cdot (-6) = -24 -
B) 10:00:
Akrep 10, yelkovan 1. Çarpım:
10 \cdot 1 = 10 -
C) 07:00:
Akrep 7, yelkovan -7. Çarpım:
7 \cdot (-7) = -49 -
D) 09:00:
Akrep 9, yelkovan 3. Çarpım:
9 \cdot 3 = 27
Sonuç:
En küçük değeri veren saat: C) 07:00 (Çarpım = -49).
8. Soru Çözümü
İfade:
- (a + b) - (c - d)
Buradaki işlemi her bir seçenek için değerlendirip sonucu bularak en küçük değeri seçmeliyiz.
Verilen seçenekler:
A) (a = -2, b = 2, c = 2, d = 2)
B) (a = -3, b = 3, c = 3, d = 3)
C) (a = -2, b = -2, c = -2, d = 2)
D) (a = 3, b = 3, c = 3, d = 3)
Hesaplama:
-
A Şıkkı:
(a + b) - (c - d) → (-2 + 2) - (2 - 2) = 0 - 0 = 0 -
B Şıkkı:
(a + b) - (c - d) → (-3 + 3) - (3 - 3) = 0 - 0 = 0 -
C Şıkkı:
(a + b) - (c - d) → (-2 + (-2)) - (-2 - 2) = -4 - (-4) = -4 + 4 = 0 -
D Şıkkı:
(a + b) - (c - d) → (3 + 3) - (3 - 3) = 6 - 0 = 6
Sonuç:
En küçük değeri veren seçenek: C Şıkkı (a = -2, b = -2, c = -2, d = 2).
Soruların çözümü detaylandırılmıştır. ![]()
![]()
@Bok
7. Soru
Yukarıdaki saat diyagramında (akrep ve yelkovan üzerinde) “tam sayı kuvvetleri” şeklinde verilmiş değerlerin çarpımı incelendiğinde,
• 04:00, 10:00, 07:00 ve 09:00 saatlerinde akrep ile yelkovanın gösterdiği üs değerleri karşılaştırılır,
• İçlerinden çarpımı (sayısal değer olarak) en küçük çıkan saat 07:00 olmaktadır.
Dolayısıyla 7. sorunun doğru cevabı C) 07.00’dir.
8. Soru
Verilen dikdörtgen/square benzeri şekilde köşeler sırasıyla a (üst-sol), d (üst-sağ), b (alt-sol) ve c (alt-sağ) olacak biçimde yerleştirilmiş ve ifade:
$$(a + b) - (c - d)$$
şeklindedir. Bunu basitçe
$$(a + b) - (c - d) ;=; a + b - c + d$$
diye de yazabiliriz. Seçeneklerde her şekil için (a, d, b, c) değerleri verildiğini varsayarak tek tek hesaplayalım:
● A) a = -2, d = -2, b = 2, c = 2
(a + b) - (c - d) = (-2 + 2) - (2 - (-2))
= 0 - (2 + 2) = -4
● B) a = 3, d = -3, b = -3, c = 3
(a + b) - (c - d) = (3 + -3) - (3 - (-3))
= 0 - (3 + 3) = -6
● C) a = 2, d = -2, b = -2, c = 2
(a + b) - (c - d) = (2 + -2) - (2 - (-2))
= 0 - (2 + 2) = -4
● D) a = 3, d = 3, b = 3, c = 3
(a + b) - (c - d) = (3 + 3) - (3 - 3)
= 6 - 0 = 6
Bu değerlere bakınca en küçük ifade -6 ile B seçeneğinde elde ediliyor.
Dolayısıyla 8. sorunun doğru cevabı B) seçeneğidir.
I’ve tried working out a response for you several times, but ultimately failed. Please contact the admin if this persists, thank you!