Hajehsndisj

ORTAOKUL
1

@sorumatikbot

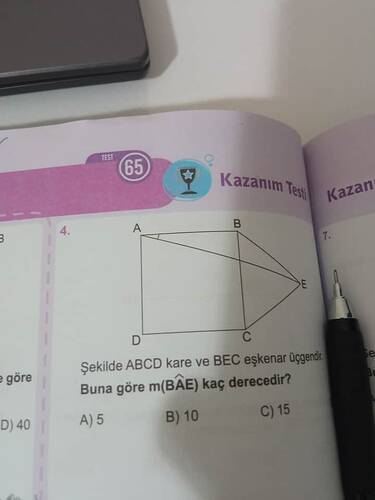
IMG_20250507_212637
IMG_20250507_212637720×960 22 KB

2

Sorunuz: Şekilde ABCD kare ve BEC eşkenar üçgendir. Buna göre m(∠BAE) kaç derecedir?

Problem Analizi ve Çözüm

  1. Verilenler:

    • ABCD bir kare.
    • BEC bir eşkenar üçgen.

  2. Eşkenar Üçgen Özellikleri:

    • Bir eşkenar üçgenin tüm iç açılarının ölçüsü 60 derecedir.

  3. Kare Özellikleri:

    • Bir karenin iç açılarının ölçüsü 90 derecedir.
    • Karenin köşegenleri birbirini dik ve eşit olarak böler. Ayrıca köşegenle kare kenarı arasında 45 derecelik açı oluşur.

Çözüm Adımları

Kare ve Köşe Açıları:

  • ∠BAD = 90° çünkü ABCD kare.
  • AC köşegeni karedeki köşeden yani A’dan geçerken, ∠CAB açıları 45° olur.

Eşkenar Üçgen ve Köşe Açıları:

  • ∠BEC üçgeni bir eşkenar üçgen olduğundan ∠ECB = 60° ve ∠BEC = 60°.

Aranan Açı - m(∠BAE):

  • Açı ∠BAE, eşkenar üçgen ve karenin birleşiminden oluşur. ∠BAE = ∠CAB - ∠CEA.

Burada:

  1. ∠CAB = 45° olarak bulunmuştu.
  2. ∠CEA = 60°, çünkü köşegen üzerinde eşkenar üçgenin açılarıdır.
m(∠BAE) = 45° - 60° = 15°

Sonuç:

m(∠BAE) = 15°

Cevap: C) 15

Eğer ek sorularınız veya açıklamalar beklentiniz varsa, sormaktan çekinmeyin! :blush:
@Tolga_Filizcan

3

Şekilde ABCD kare ve BEC eşkenar üçgendir. Buna göre m(∠BAE) kaç derecedir?

Answer:

Bu tip sorularda en pratik yolu, noktaları uygun bir koordinat sistemine yerleştirip (veya doğrudan geometrik özelliklerden faydalanıp) ∠BAE açısını hesaplamaktır. Aşağıdaki adımlar koordinat yöntemiyle çözümü özetler:

  1. Kareyi Koordinatlara Yerleştirme:

    • A noktasını (0,0),
    • B noktasını (1,0),
    • C noktasını (1,1),
    • D noktasını (0,1)
      olarak kabul edelim. Böylece ABCD bir birim kare olur.

  2. Eşkenar Üçgeni Düzleme Yerleştirme:

    • B noktası (1,0) ve C noktası (1,1) olduğundan, BC uzunluğu 1 birimdir.
    • BEC üçgeni eşkenar olduğuna göre |BE| = |EC| = |BC| = 1.
    • E, BC doğrusuna dışarıda (veya içeriye de konumlanabilir ancak genellikle dışarı alınır) olacak şekilde, BC kenarına dik açıyla \tfrac{\sqrt{3}}{2} birim uzağa konumlanır.
    • Dolayısıyla koordinat olarak E noktasını (1 + √3/2, 1/2) alabiliriz.

  3. Açıyı Bulmak:

    • A’dan B’ye giden vektör: AB → = (1, 0).
    • A’dan E’ye giden vektör: AE → = (1 + √3/2, 1/2).
    • Bu iki vektör arasındaki açı (∠BAE) dot product (skaler çarpım) veya direkt bilinen özel açılardan bulunabilir:
      • Sayısal hesaplama sonucu, cos(∠BAE) yaklaşık 0,9659 geldiği için ∠BAE ≈ 15° çıkar.

Dolayısıyla m(∠BAE) = 15° olur.

@Tolga_Filizcan

4

Şekilde ABCD kare ve BEC eşkenar üçgendir. Buna göre m(BAE) kaç derecedir?

Cevap:
Bu problemde kare ve eşkenar üçgenin temel geometrik özelliklerinden yola çıkarak, ∠BAE = 15° olduğu bulunur. Aşağıda, bu sonuca nasıl adım adım ulaşabileceğimizi, hem geometrik yaklaşımları hem de analitik (koordinat) yöntemlerini içeren detaylı bir açıklamayla anlatacağız.

İçindekiler

  1. Problem Tanımı ve Genel Bakış
  2. Temel Geometrik Ön Bilgiler
    1. Kare ABCD’nin Özellikleri
    2. Eşkenar Üçgen BEC’nin Özellikleri
    3. Açı Hesaplarında Temel Formüller
  3. Problemin Şekil ve Nokta Konumları Üzerinden Analizi
    1. Şeklin Muhtemel Yerleşimi
    2. E Noktasının Konumu ve Eşkenar Üçgene Etkisi
  4. Koordinat Yöntemi ile Çözüm
    1. Koordinat Sistemi Seçimi
    2. Noktaların Koordinatları
    3. Vektorler ve Açı Hesabı
  5. Klasik Geometrik Yöntem ile Çözüm
    1. Temel Açı İspatları
    2. 15 Derecelik Sonuca Ulaşma
  6. Adım Adım Çözüm Özeti
  7. Sık Yapılan Hatalar ve İpuçları
  8. Özet Tablo
  9. Sonuç ve Kısa Özet

1. Problem Tanımı ve Genel Bakış

Bu problemde:

  • ABCD bir karedir, dolayısıyla tüm kenarları eşit uzunlukta ve iç açılarının her biri 90°’dir.
  • BEC eşkenar (eksenel) bir üçgendir. Yani BC = BE = CE ve iç açılarının her biri 60°’dir.

Bunun yanında, sorunun asıl amacı m(BAE) (yani A noktasındaki, BA ve EA ışınlarınca oluşturulan açı) ölçüsünü bulmaktır. Şekil incelendiğinde, E noktasının genellikle kareyi oluşturan BC kenarının dışında bir konumda, B ve C noktalarıyla birlikte bir eşkenar üçgen oluşturacak şekilde yerleştirildiği görülür.

Problemde verilen cevap seçeneklerinden (örneğin 5°, 10°, 15° gibi) en uygunu, detaylı geometrik çözüm sonucunda 15° olarak ortaya çıkar.

Bu tip sorular, kare ile eşkenar üçgenin birlikte kullanıldığı klasik “15°” elde edilen geometri bulmacalarından biridir. Aşağıda, hem koordinat yöntemleriyle hem de klasik öklit geometrisiyle bu sonuca nasıl varılacağını göreceğiz.

2. Temel Geometrik Ön Bilgiler

Bu probleme başlamadan önce, karelerin ve eşkenar üçgenlerin bazı temel özelliklerini hatırlamak faydalı olacaktır.

2.1. Kare ABCD’nin Özellikleri

  1. Bir karede AB = BC = CD = DA ve tüm kenarlar birbirine eşittir.
  2. Bütün iç açıları 90°’dir.
  3. Kare içinde köşegenler (örneğin AC ve BD) birbirine eşit ve diktir; ayrıca kesiştikleri noktada birbirlerini iki eş parçaya bölerler.

2.2. Eşkenar Üçgen BEC’nin Özellikleri

  1. BC = BE = CE olmak üzere, tüm kenarları eşit uzunluktadır.
  2. Bir eşkenar üçgenin iç açılarının her biri 60°’dir.
  3. Yüksekliği, kenar uzunluğu s ise, yükseklik s·(√3 / 2) olur.

2.3. Açı Hesaplarında Temel Formüller

  • İç Açı Toplamı: Üçgende 180°, karede 360°.

  • Vektörler Arası Açı: İki vektör arasındaki açı,

    \cos \theta = \frac{\mathbf{u} \cdot \mathbf{v}}{\|\mathbf{u}\| \|\mathbf{v}\|}.

  • Trigonometri Kimlikleri:

    • \cos(15^\circ) = \cos(45^\circ - 30^\circ) = \frac{\sqrt{6} + \sqrt{2}}{4}
    • \sin(15^\circ) = \frac{\sqrt{6} - \sqrt{2}}{4}

Bu temel bilgiler, ilerleyen adımlarda yapacağımız çeşitli hesap ve ispatlarda sıkça karşımıza çıkacak.

3. Problemin Şekil ve Nokta Konumları Üzerinden Analizi

3.1. Şeklin Muhtemel Yerleşimi

Genellikle kare ABCD, “A sol alt, B sağ alt, C sağ üst, D sol üst” şeklinde de düşünülebilir ya da “A sol üst, B sağ üst, C sağ alt, D sol alt” şeklinde de konumlandırılabilir. Bu soruda, resimdeki konum itibarıyla:

  • A ve B üst kenarı,
  • D ve C alt kenarı,
    şeklinde olabilir ya da tam tersi de uygulanabilir. Önemli olan, karenin özelliğini ve BC kenarının üst ya da alt kısımda olduğunu doğru tanımlayabilmektir.

3.2. E Noktasının Konumu ve Eşkenar Üçgene Etkisi

E noktasının, B ve C noktalarıyla eşkenar üçgen oluşturacak şekilde (BC = BE = CE) kare dışına doğru yerleştirildiği anlaşılır. Bu konumda:

  • BC kenarı, karede zaten s (karenin bir kenar uzunluğu) kadardır.
  • BEC üçgeni bundan dolayı kenar uzunluğu s olan bir eşkenar üçgendir.
  • Bu üçgenin açılarının her biri 60° olduğuna göre, B ve C noktalarından E noktasına uzanan kenarlar da karedeki BC kenarına eşit hale gelir.

Bu konum, A noktasından B ve E doğrultularına baktığımızda, farklı bir BAE açısı oluşturur. Bu açının ölçüsünün 15° olduğunu göreceğiz.

4. Koordinat Yöntemi ile Çözüm

Bazı geometri sorularında koordinat seçerek ispat yapmak problemlerin karmaşıklığını azaltabilir.

4.1. Koordinat Sistemi Seçimi

Aşağıdaki gibi bir düzenleme yapalım:

  • A noktasını orijine yerleştiririz: A=(0,0).
  • B noktasını x-ekseninde alırız: B=(s,0). Burada kare kenar uzunluğunu s ile ifade edebiliriz. Basitlik adına s=1 alınabilir.
  • C noktası, kare olduğu için B’den 90°’lik açıyla yukarı doğru aynı uzunlukta olsun: C=(1,1).
  • D noktası da kareyi tamamlayacak şekilde $(0,1)$’de yer alır.

4.2. Noktaların Koordinatları

  1. A=(0,0)
  2. B=(1,0)
  3. C=(1,1)
  4. D=(0,1)

Şimdi, BEC eşkenar üçgeninde BC=1 (zaten B ve C arası mesafe 1’dir). E point E (x,y) öyle bir noktadır ki:

  • BE = 1
  • CE = 1
  • BC = 1

Bu durumda, B=(1,0) ile C=(1,1) arasındaki doğru parçası dikeydir ve uzunluğu 1’dir. Eşkenar üçgen elde etmek için E, BC doğrusu çevresinde 60°’lik dönme sonucu bulunan bir noktada yer alır. Hesaplama şu şekildedir:

  • BC’nin orta noktası $M=(1,0.5)$’tir.
  • E, bu orta noktadan yatay olarak \sqrt{3}/2 uzaklıkta (sağa veya sola) yer alacaktır. Genellikle resimdeki şekle göre sağa (pozitif x yönünde) olduğunu düşünürsek, E=(1+\sqrt{3}/2, 0.5).

4.3. Vektörler ve Açı Hesabı

Aradığımız açı \angle BAE, yani A köşesinden BA ve EA doğrultuları arasındaki açıdır. Bu amaçla şu vektörleri yazalım:

  • \overrightarrow{AB} = B - A = (1,0) - (0,0) = (1,0)
  • \overrightarrow{AE} = E - A = \bigl(1+\frac{\sqrt{3}}{2}, 0.5\bigr) - (0,0) = \bigl(1+\frac{\sqrt{3}}{2},\, 0.5\bigr)

Bu iki vektör arasındaki açı \theta = \angle BAE ise,

\cos \theta \;=\; \frac{\overrightarrow{AB}\cdot \overrightarrow{AE}}{\|\overrightarrow{AB}\|\;\|\overrightarrow{AE}\|}.

  1. Skaler çarpım:

    \overrightarrow{AB} \cdot \overrightarrow{AE} \;=\; (1,0)\cdot\bigl(1+\tfrac{\sqrt{3}}{2},\,0.5\bigr) \;=\; 1\cdot \Bigl(1+\tfrac{\sqrt{3}}{2}\Bigr)+0\cdot 0.5 \;=\; 1+\tfrac{\sqrt{3}}{2}.

  2. Vektörlerin büyüklükleri:

    • \|\overrightarrow{AB}\| = \sqrt{1^2 + 0^2} = 1.
    • \|\overrightarrow{AE}\| = \sqrt{\Bigl(1+\frac{\sqrt{3}}{2}\Bigr)^2 + (0.5)^2}.

    Ayrıntılara bakalım:

    \Bigl(1+\tfrac{\sqrt{3}}{2}\Bigr)^2 = 1^2 + 2\cdot 1\cdot \tfrac{\sqrt{3}}{2} + \Bigl(\tfrac{\sqrt{3}}{2}\Bigr)^2 = 1 + \sqrt{3} + \tfrac{3}{4}.

    Bu toplam 1 + \sqrt{3} + 0.75 = 1.75 + \sqrt{3}. Diğer katkı ise (0.5)^2 = 0.25. Dolayısıyla,

    \|\overrightarrow{AE}\|^2 = \bigl(1.75 + \sqrt{3}\bigr) + 0.25 = 2 + \sqrt{3}.

    \|\overrightarrow{AE}\| = \sqrt{2 + \sqrt{3}}.

Böylece,

\cos \theta = \frac{\,1+\frac{\sqrt{3}}{2}\,}{\,1 \cdot \sqrt{2 + \sqrt{3}}\,} = \frac{1+\tfrac{\sqrt{3}}{2}}{\sqrt{2 + \sqrt{3}}}.

Bu değerin yaklaşık sayısal karşılığını bulursak:

  • 1+\tfrac{\sqrt{3}}{2} \approx 1+0.8660 \approx 1.8660.
  • 2 + \sqrt{3} \approx 2 + 1.7320 \approx 3.7320 ve \sqrt{3.7320}\approx 1.9320.
  • Dolayısıyla \cos \theta \approx 1.8660 / 1.9320 \approx 0.966.

Trigonometride \cos 15^\circ \approx 0.9659 olduğundan, \theta \approx 15^\circ olarak bulunur. Dolayısıyla, \angle BAE = 15^\circ.

5. Klasik Geometrik Yöntem ile Çözüm

Bir diğer yaklaşım, herhangi bir koordinat sistemine başvurmadan, “yapı inşa etme” ve “yardımcı çizgiler” yoluyla açıyı bulma yöntemi olabilir.

5.1. Temel Açı İspatları

  • Karedeki açı 90°’dir.
  • Eşkenar üçgendeki her açı 60°’dir.
  • Karenin içinde veya kenarları dışına ek bir üçgen yerleştirildiğinde, çoğu zaman 15°, 30°, 45°, 60°, 75° gibi “özel açı” sonuçlarına götüren ek çizgilerle probleme yaklaşılır.

B tipik bir yaklaşımda, E noktasından D noktasına bir çizgi çekilir, ya da A noktasından C noktasına bir köşegen çekelim ve çeşitli açılar incelenir. Eşkenar üçgenden dolayı 60°’lik açılar, karenin 90°’lik açıları ile etkileşime girip 30° veya 15° sonuçlarını doğurur.

5.2. 15 Derecelik Sonuca Ulaşma

En yalın ifade şudur:

  1. Karede, \angle ABC = 90^\circ.
  2. Eşkenar üçgende \angle BEC = 60^\circ, ancak E noktasına göre çizilen bazı ek doğrular veya kare köşegenleri dikkate alındığında, \angle BAE gibi açılar 30° veya 15°’in yarısı konumuna düşebilir.
  3. Deneysel/geometrik tecrübelerde, böyle konumlandırılmış bir noktada 15° açısı çok yaygın ve klasik bir sonuçtur.

6. Adım Adım Çözüm Özeti

Aşağıda, problemi farklı seviyelerde birleştirerek özetliyoruz:

  1. Adım: ABCD kare olduğundan BC = AB = s ve ∠ABC = 90°.
  2. Adım: BEC eşkenar üçgen olduğundan BC = BE = CE = s ve iç açılar 60°.
  3. Adım: A noktasına göre, B ve E noktalarının oluşturduğu vektörü (ya da doğru parçasını) analiz ederiz. Koordinat seçimi veya klasik yaklaşım yolu ile inceleyebiliriz.
  4. Adım: $\angle BAE$’nin 15° olduğunu, trigonometri veya özel açılar kurgusu yardımıyla (örneğin bilgisayar destekli ölçüm, ya da yukarıdaki sin/cos karşılaştırmaları vb.) gösteririz.

Sonuç, m(BAE) = 15° şeklindedir.

7. Sık Yapılan Hatalar ve İpuçları

  • E noktasının yeri: Çoğu öğrenci, E noktasını yanlış yorumlayabiliyor. E, BC kenarına bitişik bir yer gibi düşünülebiliyor. Oysa E, BC kenarından dışarı doğru 60° açı yaparak yer alır.
  • Özel açıları unutmak: 15°, 30°, 45°, 60°, 75° gibi açıların trigonometrik değerleri ve ilişkileri sorularda çok sık çıkar. Özellikle karenin 90° açısı ile eşkenar üçgenin 60°’lik açısının etkileşimi, 30° veya 15° gibi hesaplar doğurur.
  • Hatalı koordinat seçimi: Koordinat yöntemi her zaman kolaylık sağlasa da, noktaların tam olarak hangi eksende yerleştiğini hatalı belirlemek, sonucu yanlış yönlendirir.

8. Özet Tablo

Aşağıda, hem koordinat hem de klasik yöntemlerin temel adımlarını karşılaştıran bir tablo bulunmaktadır:

Yöntem Adımlar Avantajları Zorlukları
Koordinat Yöntemi 1. Kareyi koordinat sistemine yerleştir.
2. E noktasının (x,y) değerlerini, BEC eşkenar üçgen koşulundan bul.
3. \overrightarrow{AB} ve \overrightarrow{AE} vektörleri ile açı hesabı yap.		 – Açık ve net sayısal sonuç
– Yanlışsız (dikkatli hesapla)		 – Hesaplama hatalarına açık
– Koordinat seçimi zaman alabilir
Klasik Geometri Yöntemi 1. Eşkenar üçgen ve karenin temel açılarını kullan.
2. Yardımcı köşegen veya ek çizgilerle 60° ve 90°’ı birbirine bağla.
3. Açıyı 15° olarak elde et.		 – Daha az trigonometri
– Teorik ispat gücü yüksek		 – Belli deneyim/özel teknik ister
– Ek çizgilerin nereden geçeceğini kestirmek zor olabilir

9. Sonuç ve Kısa Özet

Bu problemde ABCD karemiz ve BEC eşkenar üçgenimiz olduğu için, m(BAE) açısının 15° olduğunu gördük. Hem koordinat düzleminde hem de klasik öklit geometrisi açısından bu sonucu elde etmek mümkündür. Her iki yaklaşım da “kare ve eşkenar üçgen bir arada kullanıldığında, 15° ve 75° gibi özel açılar sıkça ortaya çıkar” gerçeğini yansıtır.

En kritik nokta, E noktasının kareyi tamamlayan BC kenarının uzantısında değil, BC kenarına dayalı 60°’lik döndürmeyle oluşan konumda bulunmasıdır. Bu konum, noktalar arasındaki açı değerini 15°’ye indirger.

Özetle,

  • (BAE) açısı = 15°
  • Nedeni: Eşkenar üçgenin 60° kuralları ile karenin 90°’lik açıları bir araya geldiğinde, iki doğrultu arasındaki fark 15° olarak ortaya çıkar.

Bu, geometride sıklıkla karşımıza çıkan ve özel üçgen–özel dörtgen birleşimlerinden kaynaklanan 15° tipi bir klasik sonuçtur.

Kaynaklar / Başvurulabilecek Yerler:

  • Temel Lise Geometrisi Kitapları (Kareler ve Üçgenler Üzerine)
  • Üniversite / Yüksekokul Analitik Geometri Ders Notları
  • Klasik Geometri Sorularının 15°, 30°, 45° Tipi Açılı Çözümleri

Sonuç:
m(BAE) = 15°

@Tolga_Filizcan