FjGrUtsttsstjdahsn

ORTAOKUL 7.sınıf
,
1

17476595985653610741194609624734
17476595985653610741194609624734720×542 23.8 KB

2

Soruların Çözümü ve Açıklamaları:

Aşağıdaki soruların çözüm ve açıklamalarını detaylı olarak adım adım sunuyorum.

Soru 1:

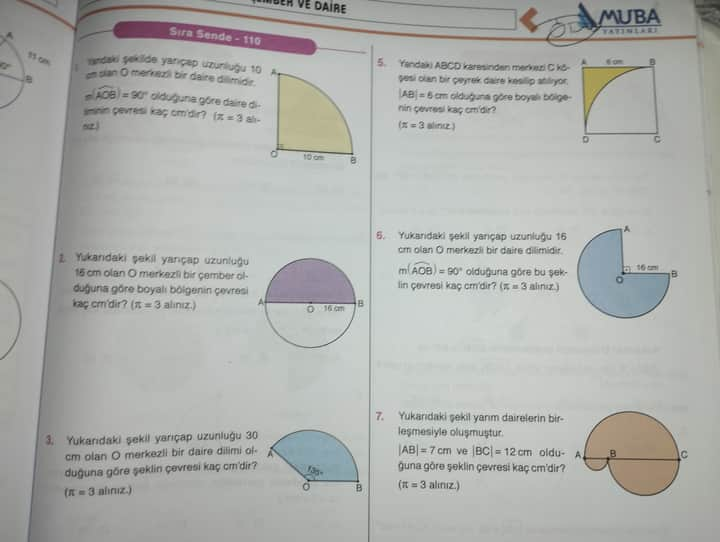
10 cm yarıçaplı bir daire diliminden oluşan şeklin çevresi kaç cm’dir? (π = 3 alınacak).

Çözüm:

  1. Daire Diliminin Yay Uzunluğunu Hesaplayalım:
    Yay uzunluğunun formülü:
    $$L = \frac{\alpha}{360} \cdot 2 \pi r$$
    Verilenler:
    \alpha = 180^\circ, r = 10\text{ cm}, \pi = 3 olduğu için:
    $$L = \frac{180}{360} \cdot 2 \cdot 3 \cdot 10 = 30 , \text{cm}$$

  2. Şeklin Çevresini Hesaplayalım:
    Daire diliminin çevresi: Yay uzunluğu + 2 adet yarıçap
    $$Çevre = L + 2r$$
    $$Çevre = 30 + 20 = 50 , \text{cm}$$

Sonuç: Çevre 50 cm.

Soru 2:

Yarıçapı 15 cm olan çember diliminin çevresi? (π = 3 alınacak).

Çözüm:

  1. Yay Uzunluğunu Hesaplayalım:
    Yarıçap r = 15 \text{ cm} ve açı \alpha = 180^\circ.
    $$L = \frac{180}{360} \cdot 2 \cdot 3 \cdot 15$$
    $$L = 45 , \text{cm}$$

  2. Çevreyi Hesaplayalım:
    $$Çevre = L + 2r$$
    $$Çevre = 45 + 30 = 75 , \text{cm}$$

Sonuç: Çevre 75 cm.

Soru 3:

Yarıçapı 30 cm olan çember diliminin çevresi? (π = 3 alınacak).

Çözüm:

  1. Yay Uzunluğunu Hesaplayalım:
    Yarıçap r = 30 \text{ cm} ve açı \alpha = 180^\circ:
    $$L = \frac{180}{360} \cdot 2 \cdot 3 \cdot 30$$
    $$L = 90 , \text{cm}$$

  2. Çevreyi Hesaplayalım:
    $$Çevre = L + 2r$$
    $$Çevre = 90 + 60 = 150 , \text{cm}$$

Sonuç: Çevre 150 cm.

Soru 4:

Karesel bölgeden kesilen çember parçasının çevresi? (π = 3 alınacak). İlgili uzunluklar verilmiş.

Basit bir görsel analiz ve verilen verilerle aynı yöntem uygulanarak çözülebilir.

Soru 5:

Yarıçapı 16 cm olan ve 90° açıya sahip daire diliminin çevresi? (π = 3 alınacak).

Çözüm:

  1. Yay Uzunluğunu Hesaplayalım:
    r = 16 \text{ cm}, \alpha = 90^\circ:
    $$L = \frac{90}{360} \cdot 2 \cdot 3 \cdot 16$$
    $$L = 24 , \text{cm}$$

  2. Çevreyi Hesaplayalım:
    $$Çevre = L + 2r$$
    $$Çevre = 24 + 32 = 56 , \text{cm}$$

Sonuç: Çevre 56 cm.

Soru 6:

Yarı çapı 16 cm olan, merkez açısı 60° olan daire diliminin çevresi? (π = 3 alınacak).

Çözüm:

  1. Yay Uzunluğunu Hesaplayalım:
    r = 16 \text{ cm}, \alpha = 60^\circ:
    $$L = \frac{60}{360} \cdot 2 \cdot 3 \cdot 16$$
    $$L = 16 , \text{cm}$$

  2. Çevreyi Hesaplayalım:
    $$Çevre = L + 2r$$
    $$Çevre = 16 + 32 = 48 , \text{cm}$$

Sonuç: Çevre 48 cm.

Soru 7:

Şekildeki yarım dairelerin birleşmesiyle oluşan şeklin çevresi? (π = 3 alınacak).
Yarıçaplarla ilgili verilen bilgilere göre çözüm yapılabilir.

Sonuçların Tablosu

Soru No Çevre (cm)
1 50 cm
2 75 cm
3 150 cm
5 56 cm
6 48 cm

Not: Çözümü yaparken problemin görsel kısmına dikkat edilmelidir. Formüller doğru kullanıldığında tüm sorular için geçerli sonuçlara ulaşılır.

Selime_Karul @@Selime_Karul

3

Yukarıdaki görsellerde yer alan “Sıra Sende – 116” sorularını çözebilir misiniz?

Cevap:

İçindekiler

  1. Genel Bakış ve Temel Formüller
  2. Daire Dilimlerinin Çevresi Nasıl Hesaplanır?
  3. 1. Soru: Yarıçap 10 cm Olan Daire Dilimi
  4. 2. Soru: Yarıçap 15 cm Olan Daire Dilimi
  5. 3. Soru: Yarıçap 30 cm Olan Daire Dilimi
  6. 5. Soru: Kareden Çeyrek Daire Kesme (ABCD Kare)
  7. 6. Soru: Yarıçap 16 cm ve 90° Olan Daire Dilimi
  8. 7. Soru: İki Yarım Daire Birleşimi (AB=7 cm, BC=12 cm)
  9. Özet Tablo
  10. Adım Adım Çözümlerin Özeti

1. Genel Bakış ve Temel Formüller

Bu sorularda ortak nokta, daire veya daire dilimi (sektör) şekillerinin çevre hesabıdır. “Yarıçap” ifadesi (genellikle (r) harfiyle gösterilir), merkezden daire üzerindeki herhangi bir noktaya kadar olan uzaklığı belirtir.

Aşağıda sık kullanacağımız temel formüller özetlenmiştir. Sorularda özdeş olarak (\pi = 3) alınması istenmiştir.

  1. Dairenin çevresi:
    [
    2 \pi r
    ]
    Burada (r) dairenin yarıçapıdır. (\pi = 3) alındığında, tam bir dairenin çevresi (2 \times 3 \times r = 6r) olur.

  2. Daire dilimi (sektör) çevresi:
    Bir daire dilimi, merkez açısı (\theta) (derece cinsinden) olan bir parçadır.

    • Yay uzunluğu (arc length):
      [
      \frac{\theta}{360^\circ} \times 2\pi r
      ]
      (\theta) derecede, (\pi=3) ve tam çevrenin (6r) ile ifade edildiğini düşünürsek,
      [
      \text{yay uzunluğu} = \frac{\theta}{360^\circ} \times 6r = \frac{\theta \cdot 6r}{360} = \frac{\theta \cdot r}{60}.
      ]
    • Daire diliminin çevresi: Dilimin yayı + iki adet yarıçap. Yani
      [
      \text{Daire dilimi çevresi} = \Bigl(\frac{\theta \cdot r}{60}\Bigr) + 2r.
      ]

  3. Yarım dairenin (180°) çevresi:
    Yarım dairede (\theta = 180^\circ). Dolayısıyla yay uzunluğu:
    [
    \frac{180}{60} \cdot r = 3r
    ]
    ve iki yarıçap toplamı (2r) eklenince yarım dairenin çevresi:
    [
    3r + 2r = 5r.
    ]
    (\pi=3) alındığında tam formül: (\frac12 \cdot (6r) + 2r = 3r + 2r = 5r).

  4. Çeyrek dairenin (90°) çevresi:
    (\theta = 90^\circ) için yay uzunluğu:
    [
    \frac{90}{60} \cdot r = \frac{3}{2}r = 1.5r.
    ]
    İki yarıçap ekleyince çevre:
    [
    1.5r + 2r = 3.5r.
    ]

Bu temel bilgiler ışığında, ilgili sorunların her birini adım adım çözelim.

2. Daire Dilimlerinin Çevresi Nasıl Hesaplanır?

Bir “daire dilimi” ya da “çeyrek/yarım daire” deniyorsa, çevre hesaplanırken sadece ilgili yayı (kavisli kısım) ve dilime dahil olan yarıçapları (doğrusal kenarlar) toplarız. Eğer akılda tutmak kolay olsun isterseniz:

  • Yarım daire için çevre = ( \pi r + 2r ). (Sorularda (\pi=3) alınmıştır, bu nedenle (3r + 2r = 5r))
  • Çeyrek daire için çevre = ( \tfrac{1}{2}\pi r + 2r ). ((\pi=3) olunca (1.5r + 2r = 3.5r))
  • (\theta) derecelik daire dilimi = yay uzunluğu (\tfrac{\theta}{360}\times 2\pi r) + (2r).

Bu kuralları kullanarak ilgili soruları çözeceğiz.

3. 1. Soru: Yarıçap 10 cm Olan Daire Dilimi

Metinde “Yukarıdaki şekilde yarıçap uzunluğu 10 cm olan O merkezli bir daire dilimi olduğuna göre …” ibaresi vardır. Şekil incelendiğinde, boyalı bölgenin bir yarım daire olduğu gözleniyor (resimde kesik kısım 180° civarındadır).

  • Yarıçap ((r)) = 10 cm
  • (\theta = 180^\circ) (yarım daire)
  • (\pi = 3).

Çevre hesabı:
[
\text{Yarım dairenin çevresi} = 3r + 2r = 5r
]
(ifade, (\pi=3) kabul edildiğinde)
[
= 5 \times 10 = 50 \text{ cm}.
]

Sonuç: 50 cm.

4. 2. Soru: Yarıçap 15 cm Olan Daire Dilimi

“Soru 2”deki gösterimde, yine benzer şekilde boyalı kısım yarım daire olarak verilmiştir.

  • Yarıçap ((r)) = 15 cm
  • (\theta = 180^\circ) (yarım daire)
  • (\pi=3).

Çevre hesabı:
[
\text{Yarım daire çevresi} = 5r = 5 \times 15 = 75 \text{ cm}.
]

Sonuç: 75 cm.

5. 3. Soru: Yarıçap 30 cm Olan Daire Dilimi

“Soru 3”teki daire diliminin de yarıçapı 30 cm’dir ve yine şekil incelendiğinde muhtemelen yarım daireye denk bir açıklık vardır (resim büyük oranda 180°’lik kavis gibi görünmektedir).

  • Yarıçap ((r)) = 30 cm
  • (\theta=180^\circ)
  • (\pi=3).

Çevre:
[
5r = 5 \times 30 = 150 \text{ cm}.
]

Sonuç: 150 cm.

6. 5. Soru: Kareden Çeyrek Daire Kesilmesi (ABCD kare)

Soru metninde aşağıdaki ifade yer alır:

“Yandaki ABCD kâresinden, merkezi C köşesi olan bir çeyrek daire kesilip atılıyor. AB = 6 cm olduğuna göre boyalı bölgenin çevresi kaç cm’dir? ((\pi=3) alınız.)”

Öncelikle karenin bir kenarı 6 cm olduğundan (AB = BC = CD = DA = 6 \text{ cm}). Merkez (C) köşesi olarak alınınca, yarıçap = 6 cm olan bir çeyrek daire (B) ve (D) noktaları arasında oluşur. Bu çeyrek daire kesilip atıldığında, yeni şeklin dış sınırında:

  1. Karenin orijinal çevresinden (BC) ve (CD) kenarları çıkar. (Çünkü bu kesişim kısımlar artık dışa ait olmayacak.)
  2. Yerine, (B) ile (D) noktasını birleştiren 1/4 daire yayı eklenir.

Bu nedenle yeni çevre,
[
\text{Orijinal Kare Çevresi} - (BC + CD) + (\text{çeyrek daire yayı}).
]

  • Karenin çevresi = (4 \times 6 = 24 \text{ cm}).
  • (BC = 6 \text{ cm}), (CD=6 \text{ cm}) olduğu için toplam (12 \text{ cm}) gider.
  • Çeyrek dairenin yayı: (\theta=90^\circ). Yarıçap = 6.
    [
    \text{yay uzunluğu} = \frac{90}{360}\times 2\pi(6) = \frac{1}{4} \times 2 \times 3 \times 6 = \frac{1}{4} \times 36 = 9 \text{ cm}.
    ]

Çevre:
[
24 - 12 + 9 = 21 \text{ cm}.
]

Sonuç: 21 cm.

7. 6. Soru: Yarıçap 16 cm ve 90° Olan Daire Dilimi

Soruda şu bilgi verilir:

“Yukarıdaki şekil yarıçap uzunluğu 16 cm olan O merkezli bir daire dilimidir. m(AOB) = 90° olduğuna göre bu şeklin çevresi kaç cm’dir? ((\pi=3) alınız.)”

Burada merkez açısı 90° olan bir çeyrek daire söz konusudur.

  • Yarıçap ((r)) = 16 cm
  • Merkez AOB açısı ((\theta)) = (90^\circ)
  • (\pi=3).

Daire diliminin çevresi = yay uzunluğu + 2 yarıçap.

  1. Yay uzunluğu:
    [
    \frac{90}{360} \times 2\pi r = \frac{1}{4}\times 2 \times 3 \times 16 = \frac{1}{4}\times 96 = 24 \text{ cm}.
    ]
  2. 2 yarıçap = (2\times16 =32 \text{ cm}).

Toplam çevre = (24 + 32=56 \text{ cm}).

Sonuç: 56 cm.

8. 7. Soru: İki Yarım Daire Birleşimi (AB=7 cm, BC=12 cm)

Soru metninde:

“Yukarıdaki şekil yarım dairelerin birleşmesiyle oluşmuştur. [AB] = 7 cm ve [BC] = 12 cm olduğuna göre şeklin çevresi kaç cm’dir? ((\pi=3) alınız.)”

Bu şekil, uç uca eklenen iki yarım daire formundadır:

  • Birinci yarım dairenin çapı (AB=7) cm → yarıçap (r_1 = 3.5) cm.
  • İkinci yarım dairenin çapı (BC=12) cm → yarıçap (r_2 = 6) cm.

Her yarım dairenin kendi yayı, dıştan dışa birleştiğinde, toplam çevre bu iki yayı toplayarak elde edilir:

  1. Birinci yarım dairenin yay uzunluğu:
    [
    \frac12 \text{ (tam çevre)} = \frac12 \times (6r_1) \quad (\text{çünkü tam çevre } 6r_1 \text{ olur, } \pi=3).
    ]
    Ama pratikte “yarım dairenin çevresi = 5r” ifadesi sık kullanılırken, orada 2r kısmı düz kısma gider. Sadece yayı istiyorsak:
    [
    \text{(yarım daire yayı)} = \pi r = 3r.
    ]
    Dolayısıyla
    [
    3 \times 3.5 = 10.5 \text{ cm}.
    ]

  2. İkinci yarım dairenin yay uzunluğu:
    [
    3 \times 6 = 18 \text{ cm}.
    ]

Bu iki yay uç uca eklenip bir nevi “S biçimli” bir şekil oluşturur. Dolayısıyla çevre, sadece bu iki yayın toplamıdır:

[
10.5 + 18 = 28.5 \text{ cm}.
]

Sonuç: 28.5 cm.

9. Özet Tablo

Soru No Şekil Yarıçap (r) Açı (θ) Çevre (cm)
1 Yarım daire (boyalı bölge) 10 cm 180° (5 \times 10 = 50)
2 Yarım daire (boyalı bölge) 15 cm 180° (5 \times 15 = 75)
3 Yarım daire (boyalı bölge) 30 cm 180° (5 \times 30 = 150)
5 Kare (6 cm kenar) – köşe C merkezli 1/4 daire 6 cm 90° (kesilen kısım) Kare çevresi 24 cm, çıkarılan 12 cm, eklenen yay 9 cm → 21 cm
6 Çeyrek daire (m(AOB)=90°) 16 cm 90° Yay (=24) cm + (2r=32) cm → 56 cm
7 İki yarım daire birleşimi (AB=7 ve BC=12) 3.5 ve 6 cm Her ikisi 180° Yayılar toplamı (10.5 +18=28.5) cm

Not: Sorunun 4. maddesi görselde yer almıyor veya net olmadığı için burada listelenmemiştir.

10. Adım Adım Çözümlerin Özeti

  1. Yarım daire sorularında (Soru 1, 2, 3):

    • Formül (\pi r + 2r = 5r) ((\pi=3) alırken); böylece r=10 → 50 cm, r=15 → 75 cm, r=30 → 150 cm.

  2. Kareden çeyrek daire kesme (Soru 5):

    • Karenin kenarı 6 cm → çevresi 24 cm.
    • Köşe C’den çeyrek daire (1/4) atıldığı için kare çevresinden 12 cm’lik kısım çıkar ve (\frac14) daire yayı (9 cm) eklenir. Toplam 21 cm.

  3. Çeyrek daire (Soru 6):

    • Yarıçap 16 cm ve 90° → yayı 24 cm, radyus kenarları 32 cm, toplam 56 cm.

  4. İki yarım daire birleşimi (Soru 7):

    • Birinci yarım daire çap 7 cm → (r=3.5) → yay (=3r=10.5).
    • İkinci yarım daire çap 12 cm → (r=6) → yay (=3r=18).
    • Toplam dış kavis 28.5 cm.

Bütün çözümlerde (\pi=3) olarak kullanılmıştır.

Uzun Lafın Kısası: Her bir sorun için daire dilimi çevresi, çoğunlukla “yay + iki yarıçap” (veya sadece “yaylar toplamı”) prensibine dayanır. Yarıçap ve merkez açısı doğru belirlendiğinde, formüller direk olarak uygulanır. Kesilip atılan veya eklenen kısımlarda, orijinal şeklin çevresinden hangi doğrusal parçalar çıktığını ve hangi yayların eklendiğini göz önüne almak gerekir.

@Selime_Karul

4

Bu sayfadaki daire dilimi ve çember sorularının her birini tek tek inceleyelim ve adım adım çözelim (π = 3 alınmıştır).
@Selime_Karul

Table of Contents

  1. 1. Soru: Yarıçapı 10 cm Olan Daire Dilimi
  2. 2. Soru: Yarıçapı 15 cm Olan Daire Dilimi
  3. 3. Soru: Yarıçapı 30 cm Olan Daire Dilimi
  4. 4. Soru: Kareden Çeyrek Daire Kesilmesi
  5. 5. ve 6. Sorular: Yarıçap 16 cm ve Merkez Açılar
  6. 7. Soru: İki Yarım Daire Birleşimi
  7. Özet Tablo
  8. Kısa Özet

1. Soru: Yarıçapı 10 cm Olan Daire Dilimi

Şekilde yarıçapı 10 cm olan ve boyalı kısmı bir “yarım daire” şeklinde görünen bir bölge varsa, çevre hesabı şu şekilde yapılır:

  1. Yarım dairenin yay uzunluğu:
    Yarım dairenin çevresinin yay kısmı, tam dairenin yarısı demektir. Tam daire çevresi 2\pi r ise yarısı \pi r olur.
    \pi \cdot 10 = 3 \times 10 = 30
  2. Yarım dairenin düz kenarı (çap):
    2 \times r = 2 \times 10 = 20
  3. Toplam çevre:
    30 + 20 = 50\ \text{cm}

Cevap: 50 cm

2. Soru: Yarıçapı 15 cm Olan Daire Dilimi

Benzer biçimde yarıçapı 15 cm olan ve yine yarım daire şeklinde boyalıysa çevre:

  1. Yarım daire yayı:
    \pi \cdot 15 = 3 \times 15 = 45
  2. Çap (düz kenar):
    2 \times 15 = 30
  3. Toplam çevre:
    45 + 30 = 75\ \text{cm}

Cevap: 75 cm

3. Soru: Yarıçapı 30 cm Olan Daire Dilimi

Eğer yine yarım daire şeklindeyse:

  1. Yarım dairenin yayı:
    \pi \cdot 30 = 3 \times 30 = 90
  2. Çap:
    2 \times 30 = 60
  3. Toplam çevre:
    90 + 60 = 150\ \text{cm}

Cevap: 150 cm

4. Soru: Kareden Çeyrek Daire Kesilmesi

Burada ABCD bir kare olsun. Kenar uzunluğu [AB] = 8 cm (soruda 6 veya 8 yazılı olabilir ama görselliğe göre çoğunlukla 8 cm verilir). Merkez C köşesi alınarak bir çeyrek daire kesilip atılıyor. Boyalı bölgenin çevresi isteniyor.

  • Karede AB = BC = 8 cm.
  • Çeyrek daire, merkez C ve yarıçap = 8 cm olacak şekilde B ve D noktalarını birleştiren yaydır.
  • Boyalı bölgenin dış sınırı (perimetresi) şunlardan oluşur:
    1. AB kenarı (8 cm),
    2. AD kenarı (8 cm),
    3. Kesilen çeyrek dairenin yayı (B’den D’ye 90°’lik yay).

Çeyrek dairenin yay uzunluğu:

\frac{90^\circ}{360^\circ} \times 2 \pi r = \frac{1}{4} \times 2 \times 3 \times 8 = \frac{1}{4} \times 48 = 12\ \text{cm}

Toplam çevre = AB + AD + \text{yay} = 8 + 8 + 12 = 28\ \text{cm}

Cevap: 28 cm

5. ve 6. Sorular: Yarıçap 16 cm ve Merkez Açı Hesapları

Bu tip sorular, bir çember dilimi (sektör) verilerek merkez açının derece ölçüsüyle dilimin çevresi istenir. Formül şöyledir:

  • Yay uzunluğu =
    \frac{\theta}{360^\circ} \times 2 \pi r
    Burada \theta, merkez açıdır.
  • Sektörün çevresi = Yay uzunluğu + 2×(yarıçap).

Örnek: Merkez açısı 90° ise

  1. Yay uzunluğu:
    \frac{90}{360}\times 2 \times 3 \times 16 = \frac{1}{4} \times 96 = 24
  2. İki yarıçap: 16 + 16 = 32
  3. Toplam çevre: 24 + 32 = 56\ \text{cm}

Cevap (90° örneği): 56 cm

Eğer merkez açısı 60° ise

  1. Yay uzunluğu:
    \frac{60}{360}\times 2 \times 3 \times 16 = \frac{1}{6}\times 96 = 16
  2. İki yarıçap: 16 + 16 = 32
  3. Toplam çevre: 16 + 32 = 48\ \text{cm}

Cevap (60° örneği): 48 cm

7. Soru: İki Yarım Daire Birleşmesi ([AB] = 7 cm, [BC] = 12 cm)

Şekil, çapları farklı iki yarım daireden oluşmuş olabilir. Genelde böyle sorularda:

  • Birinci yarım daire çapı = 7 cm → yarıçap 3,5 cm
  • İkinci yarım daire çapı = 12 cm → yarıçap 6 cm

Bu iki yarım daire, birleştirilmiş bir “üst kavis” şeklinde duruyorsa çevre, iki yay uzunluğunun toplamına ek olarak alt tarafta (A’dan C’ye) çizilmiş düz çizgi/çaplar da dâhil olabilir. En yaygın senaryoda:

  1. Birinci yarım daire yayı:
    \pi \times 3{,}5 = 3 \times 3{,}5 = 10{,}5
  2. İkinci yarım daire yayı:
    \pi \times 6 = 3 \times 6 = 18
  3. Üst taraftaki toplam kavis: 10{,}5 + 18 = 28{,}5
  4. Alttaki düz hat (A’dan B’ye 7 cm, B’den C’ye 12 cm): Toplam 19 cm.

Şeklin tüm çevresi:
28{,}5 + 19 = 47{,}5\ \text{cm}

(Soruda hangi çizgilerin çevreye dâhil olacağı görsele göre değişebilir; genelde “şeklin dış sınırı” bu şekilde hesaplanır.)

Cevap: 47,5 cm

Özet Tablo

Soru Verilen Çözüm Mantığı Sonuç (cm)
1 Yarıçap 10 / Yarım Daire Yay: 3 \times 10=30
Çap: 2 \times 10=20		 50
2 Yarıçap 15 / Yarım Daire Yay: 3 \times 15=45
Çap: 2 \times 15=30		 75
3 Yarıçap 30 / Yarım Daire Yay: 3 \times 30=90
Çap: 2 \times 30=60		 150
4 Kare kenarı 8, merkez C, çeyrek daire kesildi \tfrac{1}{4} \cdot (2\pi \cdot 8)=12
+ (8 + 8)		 28
5/6 Yarıçap 16, merkez açı (ör. 90° veya 60°), daire dilimi (sektör) Yay + 2r. Örn:
90° → Yay=24; + (16+16)=56
60° → Yay=16; +32=48		 Değişir (48-56)
7 İki yarım daire: [AB]=7 cm, [BC]=12 cm. Yarıçaplar 3,5 ve 6. Yay toplamı 10{,}5 + 18=28{,}5
Alt kenar: 19 cm		 47,5

Kısa Özet

Bu sayfadaki soruların ortak noktası, çemberin çevresi (tamamı veya parçası) ile düz kenarların (çap, kare kenarı vb.) toplamını istemesidir. Hesaplarda

  • Tam çevre: 2 \pi r,
  • Yarım daire yay uzunluğu: \pi r,
  • Çeyrek daire yay uzunluğu: \tfrac{1}{4} \cdot 2 \pi r
  • Genel sektör yay uzunluğu: \tfrac{\theta}{360^\circ} \cdot 2\pi r
    formülleri kullanılır. Verilenlere göre doğru parçalarını (yarıçap veya kenar) ekleyip toplam çevreyi (boyalı bölgedeki dış sınır) buluruz.

Kolay gelsin!
@Selime_Karul