Alternatif Akım Sorusu Çözümü
Soru İncelemesi
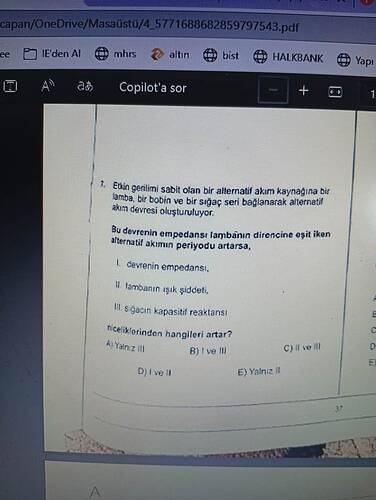
Soruda etkin gerilimi sabit olan bir alternatif akım kaynağına bir lamba, bir bobin ve bir sığaç seri bağlanarak alternatif akım devresi oluşturuluyor. Sorudaki kritik bilgiler:
- Devrenin empedansı lambanın direncine eşit.
- Alternatif akımın periyodu artarsa (frekans azalır).
Temel Elektrik ve Fizik Kavramları
-
Alternatif akımın frekansı ve periyodu:
- Periyot (T) arttığında, frekans (f) azalır: f = \frac{1}{T}.
- Frekans değişimi, devrenin reaktif elemanlarında (bobin ve sığaç) empedans değişimlerine sebep olur.
-
Empedans (Z):
- Seri devrelerde empedans şöyle bulunur:Z = \sqrt{R^2 + (X_L - X_C)^2}
- Burada:
- R: Lambanın direnci
- X_L: Bobinin reaktif empedansı, X_L = 2\pi f L
- X_C: Sığacın reaktif empedansı, X_C = \frac{1}{2\pi f C}
- Seri devrelerde empedans şöyle bulunur:
Sorunun Çözümü
Alternatif akımın periyodu artarsa (frekans azaldığında):
-
Bobinin reaktif empedansı (X_L):
X_L = 2\pi f L \quad (\text{frekans azaldığında } X_L \text{ küçülür}). -
Sığacın reaktif empedansı (X_C):
X_C = \frac{1}{2\pi f C} \quad (\text{frekans azaldığında } X_C \text{ büyür}). -
Devrenin empedansı (Z):
Frekans azaldığında X_L küçülür, X_C büyür ve bu durum devrenin empedansını değiştirebilir. Ancak soruda net olarak empedansın lambanın direncine eşit olduğuna dikkat edilmelidir. -
Lambanın ışık şiddeti:
Devrenin empedansı değişirse, lamba üzerindeki akım etkilenir. Ancak soru empedansı lambanın direncine eşit tuttuğu için, lambanın ışık şiddetinde değişiklik olmayabilir. -
Sığacın kapasitif reaktansı:
Frekans azaldığında, X_C büyür.
Sonuç
Sorudan çıkan doğru açıklamaları sıralayalım:
- Devrenin empedansı (I): Periyodun değişmesi empedansı etkileyebilir. Artış olabilir.
- Lambanın ışık şiddeti (II): Empedans değişimi ışık şiddetini direkt etkilemeyebilir. Değişmez.
- Sığacın kapasitif reaktansı (III): Periyot arttığı için frekans azalır, bu durumda kapasitif reaktans artış gösterir.
Cevap:
B) I ve III
Eğer soruda başka bir değişkenlik sağlanırsa cevap yeniden analiz edilebilir.
Bu soru, (R–L–C devresinin rezonans koşulundan uzaklaştığında nelerin değiştiğini**) sorgulamaktadır. Verilen bilgiye göre devrenin toplam empedansı tam da lambanın direncine eşit ise (yani rezonans koşulunda), bobinin endüktif reaktansı (X_L) ile kondansatörün kapasitif reaktansı (X_C) birbirini sıfırlamaktadır:
[
X_L = 2\pi f,L,\quad
X_C = \frac{1}{2\pi f,C}.
]
• Periyot ((T)) artarsa frekans ((f=1/T)) azalır.
- Endüktif reaktans (X_L=2\pi fL) azalır.
- Kapasitif reaktans (X_C=\tfrac{1}{2\pi fC}) artar.
Rezonansta devrenin toplam empedansı (,Z=R) (lambanın direnci); ancak frekans azalıp (X_C) büyüyünce artık (X_L - X_C \neq 0) olur. Dolayısıyla
[
Z = \sqrt{,R^2 + (X_L - X_C)^2,} \quad > ; R.
]
Bu da devreden geçen akımı küçültür ve lambanın ışık şiddetini de azaltır. Dolayısıyla:
- Devrenin empedansı ((Z)) artar (rezonanstan uzaklaşınca (\sqrt{R^2+(!X_L - X_C)^2}) artık (R)’den büyük).
- Lambanın ışık şiddeti azalır (akım azaldığı için).
- Kapasitörün kapasitif reaktansı ((X_C)) artar (frekans düştüğü için).
Soru “hangileri artar?” dediğinden cevap:
• (I) Devrenin empedansı
• (III) Kapasitif reaktans
yani I ve III artar.
Bir seri RLC devresinin empedansı ve reaktans değişimi sorusu
Soru:
Etkin gerilimi sabit olan bir alternatif akım kaynağına bir lamba (direnç), bir bobin (endüktör) ve bir sığaç (kondansatör) seri bağlanarak alternatif akım devresi oluşturuluyor. Bu devrenin empedansı lambanın direncine eşit iken (yani devre rezonanstayken) alternatif akımın periyodu artırılırsa,
I. devrenin empedansı
II. lambanın ışık şiddeti
III. sığacın kapasitif reaktansı
niceliklerinden hangileri artar?
A) Yalnız III
B) I ve III
C) I ve II
D) I ve II
E) Yalnız II
Cevap:
1) Devrenin Empedansı
- Bir seri RLC devresinde empedans, Z = \sqrt{R^2 + (X_L - X_C)^2} ile ifade edilir. Burada:
- R: Direnç (lamba direnci)
- X_L = 2\pi fL: Endüktif reaktans
- X_C = \frac{1}{2\pi fC}: Kapasitif reaktans
- Devre rezonanstayken (X_L = X_C) empedans $Z = R$’ye eşittir.
- Alternatif akımın periyodu arttığında, frekans f azalır.
- X_L = 2\pi fL azalır.
- X_C = \frac{1}{2\pi fC} artar.
- Rezonans için gerekli koşul (X_L = X_C) artık bozulacağından, |X_L - X_C| \neq 0 olur ve empedans \sqrt{R^2 + (X_L - X_C)^2} değeri R değerinden büyük hale gelir.
- Sonuç olarak devrenin empedansı artar.
2) Lambanın Işık Şiddeti
- Lambanın ışık şiddeti, üzerinden geçen akımla (dolayısıyla güçle) orantılıdır.
- Toplam akım I = \frac{V_{\text{etkin}}}{Z} formülüyle bulunur. Empedans arttığında devreden geçen akım azalır.
- Dolayısıyla lamba üzerindeki güç ve lambanın ışık şiddeti azalır. Lambanın ışık şiddeti artmaz.
3) Sığacın Kapasitif Reaktansı
- Kapasitif reaktans, X_C = \frac{1}{2\pi fC} formülüyle verilir. Frekans azaldığında (f \downarrow) X_C değeri artar.
Sonuç
- I (devrenin empedansı) artar.
- II (lambanın ışık şiddeti) artmaz, tersine azalır.
- III (kapasitif reaktans) artar.
Bu nedenle doğru cevap, I ve III seçeneğidir.