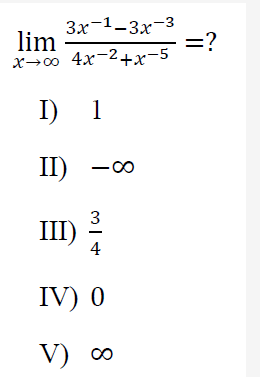Muhammed_Burak_TÜRKY said
Answer:
To find the limit
$$\lim_{{x \to \infty}} \frac{3x^{-1} - 3x^{-3}}{4x^{-2} + x^{-5}},$$
we need to determine the behavior of the function as ( x ) approaches infinity.
-
Rewrite the expression:
-
Rewrite ( x^{-n} ) as ( \frac{1}{x^n} ).
\frac{3x^{-1} - 3x^{-3}}{4x^{-2} + x^{-5}} = \frac{\frac{3}{x} - \frac{3}{x^3}}{\frac{4}{x^2} + \frac{1}{x^5}}
-
-
Factor out the dominant term in both the numerator and denominator:
-
In the numerator, the dominant term as ( x \to \infty ) is ( \frac{3}{x} ).
-
In the denominator, the dominant term as ( x \to \infty ) is ( \frac{4}{x^2} ).
Factor out ( \frac{1}{x} ) in the numerator and ( \frac{1}{x^2} ) in the denominator:
\frac{\frac{3}{x} \left(1 - \frac{1}{x^2}\right)}{\frac{4}{x^2}\left(1 + \frac{1}{4x^3}\right)}
-
-
Simplify the expression by canceling out common terms:
-
Simplify the expression:
\frac{3x^{-1} \left(1 - x^{-2}\right)}{4x^{-2} (1 + x^{-3}/4)} = \frac{3}{4} x \left(1 - x^{-2}\right) \left(1 + x^{-3}/4\right)^{-1}
As ( x \to \infty ), terms with higher-degree negative exponents (( x^{-2}, x^{-3} )) will approach 0:
\frac{3}{4} \left(1 - 0\right) \left(1 + 0\right)^{-1} = \frac{3}{4} -
Therefore, the limit is:
$$\boxed{\frac{3}{4}}$$