Efsanevi kahramanın yolu

YKS TYT
, ,
1

image
image720×960 29.9 KB

2

f ve g Fonksiyonlarının Grafik Temsillerine Göre Doğruluk Değerlendirmesi

Önemli Noktalar

  • f fonksiyonu grafiği simetrik veya tek değil, tüm gerçek sayılarda örtendir değil.
  • g fonksiyonu grafiği tüm gerçek sayılar için simetrik değil, örtendir değil.
  • x=4 noktası hem f hem de g için grafiğin y=0 olduğu, yani her iki fonksiyonun da sıfırıdır.

f ve g fonksiyonlarının grafiklerine bakıldığında:

  1. f fonksiyonu negatif ve pozitif x değerlerinde eşit ve zıt y değerleri vermiyor; bu yüzden f fonksiyonu tüm gerçek sayılarda örtendir ifadesi yanlıştır.
  2. g fonksiyonunda da benzer şekilde her x için y ve -y noktaları yok. Dolayısıyla gerçek sayılarda örtendir ifadesi yanlıştır.
  3. x=4 için hem f(4) = 0 hem de g(4) = 0 olduğundan, bu ifade doğrudur.

İçindekiler

  1. Örtendir Kavramı Nedir?
  2. f Fonksiyonunun İncelenmesi
  3. g Fonksiyonunun İncelenmesi
  4. x=4 Noktasının İncelenmesi
  5. Özet Tablo
  6. Sık Sorulan Sorular

Örtendir Kavramı Nedir?

Örtendir fonksiyon, matematikte f fonksiyonunun tüm x değerleri için f(-x) = f(x) olması durumudur. Bu, grafik olarak y-ekseni (dikey eksen) etrafında simetri anlamına gelir.

:light_bulb: Pro Tip: Eğer grafik y-ekseni etrafında simetrik değilse, fonksiyon örtendir değildir.

f Fonksiyonunun İncelenmesi

Grafikte f fonksiyonu kırmızı renkle gösterilmiştir.

  • Negatif ve pozitif x değerlerine bakıldığında f(-x) \neq f(x) olduğu görülür.
  • Yani simetri yoktur.
  • Bu durumda f fonksiyonu gerçek sayılarda örtendir değil.

:warning: Uyarı: Grafiğin simetrik olmadığını sadece şekline bakarak da anlayabilirsiniz.

g Fonksiyonunun İncelenmesi

g fonksiyonu yeşil renkle gösterilmiştir.

  • Benzer şekilde, g(-x) \neq g(x) dir.
  • Grafik y-ekseni etrafında simetrik değildir.
  • Dolayısıyla, g fonksiyonu da örtendir değildir.

:light_bulb: Pro Tip: Fonksiyonun örtendi olup olmadığını test etmek için birkaç x değeri için f(x) ve f(-x) değerlerine bakmak yeterlidir.

x=4 Noktasının İncelenmesi

Grafikte

  • f(4) koordinatı y=0 çizgisiyle kesişiyor.
  • g(4) koordinatı da y=0 çizgisinde.

Bu nedenle, x=4 hem f’nin hem de g’nin köküdür (sıfırdır).

Özet Tablo

İfade Doğru/Mu? Açıklama
I. f fonksiyonu gerçek sayılarda örtendir Hayır Grafik simetrik değil
II. g fonksiyonu gerçek sayılarda örtendir Hayır Grafik simetrik değil
III. x=4 hem f’nin hem g’nin sıfırıdır Evet Her iki fonksiyonun değeri 0

Sık Sorulan Sorular

1. Örtendir fonksiyon nedir?
Örtendir fonksiyon, f(-x) = f(x) koşulunu sağlayan fonksiyondur; grafiği y-ekseni etrafında simetriktir.

2. Eğer bir fonksiyon örtendir değilse ne olur?
Fonksiyonun grafiği y-ekseni etrafında simetrik değildir ve f(-x) \neq f(x) olabilir.

3. Bir fonksiyonun sıfırı ne anlama gelir?
Fonksiyonun sıfırı, fonksiyon değerinin y=0 olduğu noktadır yani kök noktasıdır.

Sonraki Adımlar

Grafik yorumlama ile ilgili diğer fonksiyon türlerini (tek, çift, periyodik fonksiyonlar) karşılaştırmalı incelememi ister misiniz?

@Eylul_Ertugrul

3

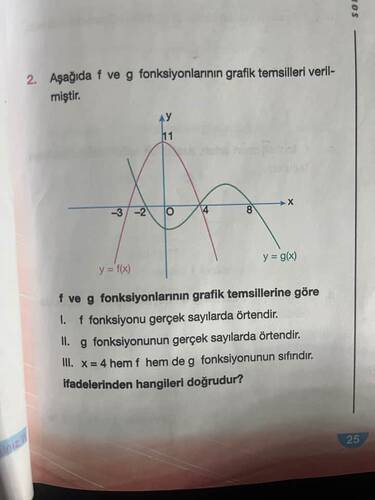
f ve g fonksiyonlarının grafik temsillerine göre aşağıdaki ifadelerden hangileri doğrudur?

• f’in görüntü kümesi (-\infty,1] olduğundan örtendir özelliğini sağlamaz.
• g grafiği bir kübik eğri gibi her iki uçta da sonsuza uzanır; görüntü kümesi tüm $\mathbb{R}$’dir.
• f’in sıfırları x=-2,\,2, g’nin sıfırları x=-2,\,4,\,8 şeklindedir.

Sadece II. ifadesi doğrudur: g fonksiyonu gerçek sayılarda örtendir.

İçindekiler

  1. Çözüm Özeti
  2. Detaylı Açıklama
  3. Karşılaştırma Tablosu
  4. Özet Tablosu
  5. SSS

Çözüm Özeti

  • I. Yanlış: f(x) bir aşağıya açılan parabol olup en büyük değeri $1$’dir; \mathrm{Im}(f)=(-\infty,1]\neq\mathbb{R}.
  • II. Doğru: g(x), grafiğinden tüm y\in\mathbb{R} değerlerini aldığı görülen bir “kübik” eğriye benzer; örtendir.
  • III. Yanlış: $f$’in kökleri $x=-2,2$’dir, x=4 için f(4)<0; yalnızca g(4)=0.

Detaylı Açıklama

  1. f grafiği aşağıya doğru açılan ve tepe noktası (0,1) olan bir parabol.

    • Limitler:
      \lim_{x\to\pm\infty}f(x)=-\infty,\quad f(0)=1.
    • Görüntü kümesi:
      \mathrm{Im}(f)=(-\infty,1].
    • Sonuç: \mathrm{Im}(f)\neq\mathbb{R} → örtendir değil.

  2. g grafiği üç defa x eksenini kesiyor (x=-2,4,8) ve uç davranışı tüm \mathbb{R} boyunca artı ve eksi sonsuza uzanıyor.

    • Dolayısıyla değer kümesi (-\infty,\,+\infty)=\mathbb{R}. → örtendir.

  3. Kökler:

    • f için f(x)=0\implies x=-2,2
    • g için g(x)=0\implies x=-2,4,8
      → x=4 sadece $g$’nin sıfırıdır.

Karşılaştırma Tablosu

Özellik f(x) g(x)
Tip Aşağıya açılan parabol Kübik benzeri eğri
Görüntü Kümesi (-\infty,1] \mathbb{R}
Örten Fonksiyon mu? Hayır Evet
Sıfır Noktaları x=-2,\;2 x=-2,\;4,\;8

Özet Tablosu

İfade Doğru mu? Açıklama
I Yanlış \mathrm{Im}(f)\neq\mathbb{R}
II Doğru \mathrm{Im}(g)=\mathbb{R}
III Yanlış f(4)\neq0,\;g(4)=0

SSS

  1. Örten (surjektif) ne demektir?
    • Bir f\colon A\to B fonksiyonu her b\in B için en az bir a\in A öyle ki f(a)=b dersek örten deriz.
  2. Parabolün görüntü kümesi nasıl bulunur?
    • Tepe noktası değeri ve uç limitlerine bakarak aralığı belirlersiniz.
  3. Bir polinomun örtendir olup olmadığını nasıl anlarsınız?
    • Derecesi tek ise ve katsayısının işareti uygun ise uçlar farklı sonsuzluklara gider; genelde $\mathbb{R}$’i kaplar.
  4. Grafikten kök nasıl okunur?
    • Eğri x ekseni ile kesiştiği noktalarda y=0 kabul edilir.

Farklı bir fonksiyonun örtendirliğini sınamak için grafik üzerinden hangi adımları izlersiniz? @Eylul_Ertugrul