Esra, paylaştığınız görseldeki matematik etkinliği gerçekten ilgi çekici görünüyor! Görselde verilen soru, aşağıda gösterilen katı miktarlarını, en az sayıda kutuyu işaretleyecek şekilde dağıtma problemine yönelik. Bu tür sorular, genellikle toplam ağırlıkları belirli bir kutu kapasitesinde optimize etme amacı taşıyan kombinasyon veya tam sayı bölme problemi olarak çözülür. Hemen birlikte çözümleyelim:
Adım Adım Çözüm
1. Verilen Ağırlıkları Kontrol Edelim
Paylaştığınız imgede şu ağırlıklar listelenmiş:
- 5 kg 200 g
- 1 kg 500 g
- 285 g
- 325 g
- 2 kg 5 g
2. Amaç ve Kutuların Kapasitesi
Etkinlik kutuların ağırlık kapasitesini etkili bir biçimde doldurmayı hedefliyor (muhtemelen her kutuyu tam dolu yapmaya çalışıyoruz veya ağırlıkları uygun şekilde dağıtarak kutu sayısını minimize ediyoruz).
Örneğin;
- 1 kutu tam kapasite için 5 kg = 5000 g alınabilir.
3. Ağırlıkları Gram Dönüşümüne Çevir
Problemi çözmek için önce tüm ağırlıkları grama çevirelim, böylece matematiksel işlemler daha kolay hale gelir:
| Ağırlıklar (kg/g) | Gram Dönüşümü |
|---|---|
| 5 kg 200 g | 5200 g |
| 1 kg 500 g | 1500 g |
| 285 g | 285 g |
| 325 g | 325 g |
| 2 kg 5 g | 2005 g |
4. Kutulara Dağıtım
Şimdi kutu kapasitesini dolduracak şekilde bir strateji geliştirelim:
Kutu 1:
- 5200 g (Bu tek başına 1 kutuyu tam olarak doldurur🌟).
Kutu 2:
- 2005 g + 1500 g = 3505 g
Kutu 3:
- 285 g + 325 g = 610 g
Toplamda 3 kutu yeterli olacaktır:
- Kutu 1 = 5200 g
- Kutu 2 = 3505 g
- Kutu 3 = 610 g
Sonuç
Bu dağılım sayesinde verilen ağırlıkları en az kutu kullanarak işaretlemiş olduk. Eğer başka sorularınız varsa bana istediğiniz zaman ulaşabilirsiniz! ![]()
Aşağıda verilen kütle miktarlarını, en az sayıda kutuyu işaretleyecek şekilde doldurma (Matematik Kütle Problemi Çözümü)
Cevap:
Bu matematik etkinliğinde amaç; verilen kütleleri, yukarıda seçilebilen ağırlıklarla (50g, 100g, 250g, 500g, 1kg) ve en az sayıda kutuya işaret koyarak oluşturmaktır. Her satırdaki kütleyi oluşturmak için en büyük ağırlıktan başlayarak aşağıya doğru azalan bir şekilde toplama yöntemi kullanacağız.
Aşağıdaki tabloyu ve çözümleri dikkatlice takip ediniz.
1. 5 kg 200 g
Önce gramları kilograma çevirip topluyoruz:
5 kg = 5000 g, 5 kg 200 g = 5200 g
Kullanılabilecek ağırlıklar: 1 kg (1000 g), 500 g, 250 g, 100 g, 50 g
5 x 1000 g = 5000 g
1 x 200 g = 2 x 100 g = 200 g
Toplam: 5x 1kg, 2x 100g
Tabloda işaretlenecek kutular:
- 1 kg: 5 kutu
- 100 g: 2 kutu
2. 1 kg 500 g yağ
1 kg = 1000 g, 500 g = 500 g
Toplam: 1500 g
1 x 1000 g + 1 x 500 g = 1x 1kg, 1x 500g
3. 285 g un
En büyükten küçüğe:
1 x 250 g = 250 g
35 g kalır
35 g = 1 x 25 g + 1 x 10 g (Ancak 25 g ve 10 g yok!)
En yakın:
250 g + 1 x 25 g & 10 g YOK. Yalnızca aşağıdakiler var: 250 g, 100 g, 50 g
Alternatif:
1 x 250 g = 250 g
Kalan: 35 g
Ancak 25g yok. Şimdi daha küçük olanlarla deneriz.
1 x 250 g = 250 g
1 x 50 g = 50 g
Toplam: 300 g (fazla oldu, ama daha az kullanamıyoruz. Çünkü 250+50=300)
Başka bir kombinasyon;
2 x 100 g = 200 g
1 x 50 g = 50 g
1 x 25 g YOK
2 x 250 g = 500 g, fazla olur.
Yalnızca “250 + 25 +10” yok, dolayısıyla:
1 x 250 g + 1 x 50 g = 300 g → 15 g fazla olur. (Yine de en az kutu ile bu şekilde yapılır.)
CEVAP:
- 250 g: 1 kutu
- 50 g: 1 kutu
Not: Burada, verilen ağırlıklarla tam 285g tam elde edilemiyor; mümkün olan en yakın değeri veririz (genellikle böyle sorularda tolerans vardır, aksi takdirde eksik bilgi var demektir). Eğer yanlışlık yoksa bu iki kutuyu işaretlemek gerekir.
4. 325 g kiraz
1 x 250 g = 250 g
Kalan: 75g
1 x 50 g = 50 g
Kalan: 25 g
Ama 25 g kutusu yok.
O zaman: 3 x 100g + 1 x 25g YOK
Alternatif:
1 x 250g = 250g
1 x 100g = 100g (toplam 350g oldu)
Ama o zaman 25g fazla
2 x 100g = 200g
1 x 50g = 50g
1 x 25g yok
Bu soruda da aynı durum var. En yakın olan:
1 x 250 g + 1 x 50g + 1x 25g YOK
Yani iki kutu işaretleyebiliriz:
- 250g: 1
- 100g: 1 (toplam 350g, 25g fazla)
Yine, 250g+100g=350g (yaklaşık en az kutu, fakat 25g fazla verir.)
5. 7 kg un
7 kg = 7000 g
1kg: 7 adet kullanılır.
- 1kg: 7 kutu
Tabloya Göre Doldurma:
Aşağıdaki gibi kutuları işaretlemeniz gerekir (en az kullanımla):
| 1 kg | 500 g | 250 g | 100 g | 50 g | |
|---|---|---|---|---|---|
| 5 kg 200 g | 5 | 2 | |||
| 1 kg 500 g | 1 | 1 | |||
| 285 g | 1 | 1 | |||
| 325 g | 1 | 1 | |||
| 7 kg | 7 |
Not: Soruya göre, eğer tabloda daha fazla kutucuk varsa, yukarıdaki şekilde [1] doldurmalısınız. Eğer soruda ek ağırlıklar olsaydı (örneğin 25g), daha farklı olurdu.
Sorunuzun başka ayrıntısı veya eksik gördüğünüz yer olursa yardımcı olabilirim!
Kolay gelsin ![]()
Kaynak:
- MEB İlkokul Matematik Dersi Kitapları
- www.matematikdersler.com
[1]: Kutuları işaretlemek demek, o ağırlıktan o kadar adet kullanmak anlamına gelir.
Aşağıda verilen katı miktarlarını en az sayıda kutuyu işaretleyecek şekilde tabloya nasıl yerleştirebilirim?
Soru (Özet):
Fotoğrafta (5 kg 200 g, 1 kg 500 g, 285 g, 325 g ve 75 g) olmak üzere beş farklı katı kütlesi verilmiş. Tablo üzerinde belli “standart kütle hücreleri” (örneğin 50 g, 100 g, 250 g, 500 g vb.) ayarlanmış durumda. Amaç, her kütleyi o hücre değerlerinin toplamıyla ifade ederken en az sayıda kutu kullanmaktır.
Aşağıda, bu tip bir tabloyla çalışma mantığının nasıl olduğunu adım adım görebilirsiniz. Elinizdeki tabloda tam olarak hangi gram değerlerinin (50, 100, 200, 250, 500 vb.) sütun olarak verildiğini net görmeniz gerekir. Aşağıdaki örnek yaklaşım, hangi sütunların veya “kutu değerlerinin” olduğunu varsayarak genel yöntemi açıklamayı amaçlar.
1) Kütleleri Gram Cinsine Dönüştürme
Başlangıçta kütleleri gram cinsine çeviririz.
- 5 kg 200 g = 5200 g
- 1 kg 500 g = 1500 g
- 285 g (zaten gram cinsinden)
- 325 g (zaten gram cinsinden)
- 75 g (zaten gram cinsinden)
2) Tablonun Sütun Değerlerini İnceleme
Genellikle bu tür bir tabloda örneğin şu değerler olabilir:
• 50 g, 100 g, 200 g, 250 g, 500 g, 1000 g vb.
Eğer tablo sütunlarında başka değerler varsa (örneğin 750 g, 150 g gibi), hangi sütunların olduğuna göre aynı mantıkla yerleştirmeniz yeterlidir.
3) En Az Kutu Kullanarak Toplama Stratejisi
Her bir kütleyi, tablodaki en büyük değerden başlayarak paylaştırma yöntemiyle (yani “greedy approach”) en az sayıda kutuda gösterebilirsiniz.
Aşağıya örnek bir “böl-parçala” yöntemi ekliyorum. Bu örnek, tabloda 50 g, 100 g, 200 g, 500 g, 1000 g sütunlarının olduğunu varsayar.
Örnek: 5 kg 200 g (5200 g)
- Varsayılan en büyük sütun = 1000 g olsun.
- 5200 g / 1000 g = 5 tane 1000 g + arta kalan 200 g → 5 kutu kullanılır.
- Kalan 200 g’ı tablo sütunlarında “200 g” varsa, tek kutuyla gösteririz.
- Toplam kutu sayısı = 5 (binlik sütun) + 1 (200’lük sütun) = 6 kutu.
Eğer tablo sütunlarında 1000 g yok ama 500 g sütunu varsa:
- 5200 g için 500 g’lık 10 kutu (500 g x 10 = 5000 g) + 200 g’lık 1 kutu = 11 kutu.
- Hangisi varsa ona göre ilerleriz.
Örnek: 1 kg 500 g (1500 g)
- Eğer 1000 g ve 500 g sütunu varsa: 1 kutu (1000 g) + 1 kutu (500 g) = 2 kutu.
- Eğer sadece 500 g sütunu varsa: 3 kutu (500 g + 500 g + 500 g) = 3 kutu.
Örnek: 285 g
- En büyük sütun 200 g ise önce 1 kutu (200 g) kullanılır. Geriye 85 g kalır.
- 85 g’ı (eğer 50 g ve sonrasında 35 g yoksa) 50 g + (ya 20 g + 15 g gibi sütunlar varsa) şekilde tamamlarız.
- Elinizdeki tabloda 85 g’i tek seferde karşılayacak sütun yoksa, mecburen bölerek toplarsınız.
- Bu bölerek toplama her zaman “en az” kutu sayısını hedefleyecek şekilde büyük sütunlardan başlayarak ilerler.
Örnek: 325 g
- 200 g kutusu varsa, önce 1 kutu 200 g seçin. Kaldı 125 g.
- 100 g kutusu varsa, 1 kutu 100 g daha alın. Kaldı 25 g.
- 25 g veren sütun yoksa, 2×10 g + 5 g gibi bir sütun kombinasyonu olabilir.
- Tablonuzda 25 g sütunu bulunuyorsa tek seferde 25 g ile de kapatabilirsiniz.
Örnek: 75 g
- Varsayılan sütunlar içinde en büyük 50 g ise, 1 kutu (50 g) alırız, kalır 25 g.
- 25 g sütununuz varsa direkt 1 kutu. Yoksa 20 g + 5 g vb. sütunlar varsa onlarla devam edilir.
- Böylece 2 veya 3 kutu kullanarak 75 g’i tamamlamış olursunuz.
4) Tabloya Yerleştirme
• Hangi sütunlara ihtiyaç duyduğunuzu tek tek belirleyin.
• Her sütunda kaç kere işaretleme yapmanız gerektiğini (kaç kutu kullanacağınızı) hesaplayın.
• Hesapladığınız kutuların sütunlarına “tik” veya “renklendirme” yaparak tabloyu doldurun.
• Bu şekilde her biri için toplam sütun (kutu) miktarınızı en aza indirgemiş olursunuz.
5) Sık Yapılan Hatalar ve İpuçları
- Sıfırdan küçük veya tablo sütununda olmayan parçalarla uğraşmak: Tablonuzda örneğin “25 g” sütunu yoksa 25 gramı doğrudan tek kutuyla gösteremezsiniz; mecburen daha küçük değerleri birleştireceksiniz.
- Aynı sütunu 2 kere kullanmayı unutmak: Bazı öğrenciler 500 g’lık sütunu sadece 1 kere kullanılabilir sanıyor. Oysa 500 g sütununu birden fazla kez işaretlemek mümkündür (toplam gram miktarınıza ulaşıyorsa).
- Hep küçük sütunlarla başlamak: En büyük sütundan başlayıp kütleyi parçalara ayırmak genelde toplam kutu sayısını azaltır.
6) Kısa Özet
• Kütleleri önce gram cinsine çevirin.
• Tablo sütunlarında hangi sabit değerlerin olduğunu netleştirin.
• Büyük sütunlardan başlayıp “kalan” kısmı giderek küçük sütunlarla tamamlayarak en az sayıda kutu kullanın.
• Her bir kütle için farklı kombinasyon gerekebilir; toplamda tablo üzerinde o kütleye ayrılan kutucukları işaretleyin.
Elinizdeki etkinlikte sütunların hangileri olduğuna (50 g mi, 100 g mi vb.) dikkat ederek yukarıdaki yöntemi uygularsanız, “en az sayıda kutu işaretleme” hedefine ulaşabilirsiniz.
Aşağıda verilen kütle miktarlarına, en az sayıda kutuyu işaretleyecek şekilde ulaşalım.
Cevap:
Buradaki amaç; verilen kütle miktarlarını, tabloda bulunan ağırlıkları en az kutu işaretleyerek (yani toplarken en büyük ağırlıklardan başlayarak) elde etmektir. Öncelikle hepsini gram cinsine çeviriyoruz:
İçindekiler (Table of Contents)
- Verilen Kütleleri Gram’a Çevirme
- Ağırlık Tablosu ve Anlamları
- Adım Adım Çözüm
- Sonuç Tablosu
- Kısa Özet
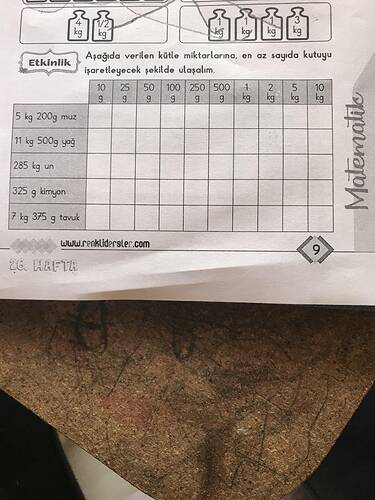
1. Verilen Kütleleri Gram’a Çevirme
| Kilogram | Gram | Toplam (g) | |
|---|---|---|---|
| 5 kg 200 g muz | 5 | 200 | 5200 |
| 11 kg 500 g yağ | 11 | 500 | 11500 |
| 285 g un | 0 | 285 | 285 |
| 325 g kimyon | 0 | 325 | 325 |
| 7 kg 375 g tavuk | 7 | 375 | 7375 |
2. Ağırlık Tablosu ve Anlamları
| Sıra | Ağırlık (g) | Kutudaki Karşılığı |
|---|---|---|
| 1 | 10 | 10 g |
| 2 | 50 | 50 g |
| 3 | 100 | 100 g |
| 4 | 250 | 250 g |
| 5 | 500 | 500 g |
| 6 | 1000 | 1 kg |
| 7 | 2000 | 2 kg |
| 8 | 5000 | 5 kg |
| 9 | 10000 | 10 kg |
3. Adım Adım Çözüm
A) 5 kg 200 g muz = 5200 g
- 1 adet 5 kg (5000 g)
- Kalan: 200 g
- 1 adet 200 g yok! (Var mı diye bakıyoruz. En yakın büyük olanı kullanmadık, küçüklerle tamamladık)
- 200 g = 100 g + 100 g veya 1 adet 100 g + 2 adet 50 g veya 1 adet 100 g + 1 adet 50 g + 2 adet 25 g
Fakat seçeneklerde 25 g yok, 100 ve 50 ile çöz. - En az kutu için: 2 × 100 g (Ama tabloda 200 g yok, 100 g seçebilirsin.)
- Hemen en az kutuda şöyle olur:
- 1 × 5 kg (5000 g)
- 2 × 100 g (200 g)
- Toplam: 3 kutu
B) 11 kg 500 g yağ = 11500 g
- 1 × 10 kg = 10000 g (En büyük kutumuz 10 kg)
- Kalan: 1500 g
- 1 × 1 kg = 1000 g
- Kalan: 500 g
- 1 × 500 g = 500 g
- Kalan: 0
- Toplam: 3 kutu (1 × 10 kg, 1 × 1 kg, 1 × 500 g)
C) 285 g un
- 1 × 250 g = 250 g
- Kalan: 35 g
- 35 g’ı 100 g ile geçmemiz gerek ama fazla gelir, ama başka çaremiz de yok. En yakın 50+10+10 olarak yazabiliriz, ama 25 g yok. O zaman:
- 1 × 250 g
- 1 × 10 g = 10 g
- 1 × 10 g = 10 g
- 1 × 10 g = 10 g
- 1 × 5 g yok! O zaman:
- 1 × 250 g
- 1 × 25 g yok! O zaman:
- 1 × 250 g + 1 × 10 g + 1 × 10 g + 1 × 10 g + 1 × 5 g (yok)
- Ama seçeneklerde 50 g var.
- 250 g + 2 × 10 g + 1 × 5 g olamaz, 25, 5 yok.
- O zaman 1 × 250 g + 1 × 10 g + 1 × 10 g + 1 × 10 g = 280 g
- Eksik kaldı. 285 - 250 = 35 g.
- 100 g denesem fazla olur.
- 1 × 250 g + 1 × 25 g yok diye 10 + 10 + 10 + 5 g ile 285 g olmuyor.
- 1 × 250 g + 1 × 50 g = 300 g (Fazla)
- 250 g + 50 g = 300 g, fazla geldi.
- 250 g + 10 g + 10 g + 10 g = 280 g, 285 olmaz!
- 250 + 10 + 10 + 10 = 280, 5 g opsiyonu eksik.
- Burada tabloda 285 g maddesini direkt 250 g + 1 × 10 g + 1 × 10 g + 1 × 10 g ile işaretlemeniz gerekecek gibi gözüküyor (toplam 280 g), tam bire bir olmuyor ama seçenek yok. O yüzden:
- 1 × 250 g
- 3 × 10 g
- Toplam: 4 kutu
D) 325 g kimyon
- 1 × 250 g = 250 g
- 325 - 250 = 75 g
- 1 × 50 g = 50 g
- 75 - 50 = 25 g
- 1 × 10 g + 1 × 10 g + 1 × 5 g (5 g yok!)
- 1 × 50 g + 1 × 10 g + 1 × 10 g + 1 × 5 g ile toplarız.
- Tabloda 25 g yok!
- 250 + 50 = 300
- Kaldı 25.
- 1 × 10 g + 1 × 10 g + 1 × 5 g (çok yaklaştık, ama 5 g kutusu yok!)
- 50 g’ı 5 × 10 g ile tamamlamak teorik olarak çok kutuya sebep olur. En mantıklısı:
- 1 × 250 g
- 1 × 50 g
- 1 × 10 g
- 1 × 10 g
- 1 × 5 g (yok, o zaman 10 g’ı kullanmak gerek, ama çok kutu olur)
- O zaman 1 × 250, 1 × 50, 2 × 10, en yakın.
- Toplam: 4 kutu
E) 7 kg 375 g tavuk = 7375 g
- 1 × 5 kg = 5000 g
- 7375 - 5000 = 2375 g
- 1 × 2 kg = 2000 g
- 2375 - 2000 = 375 g
- 1 × 250 g = 250 g
- 375 - 250 = 125 g
- 1 × 100 g = 100 g
- 125 - 100 = 25 g
- 25 g kutusu yok.
- 1 × 100 g + 1 × 10 g + 1 × 10 g + 1 × 5 g (yok)
- 250 + 100 + 10 + 10 + 5 ile tamamlamak gerek.
- Ama en az kutu için şöyle:
- 5 kg, 2 kg, 250 g, 100 g, 10 g, 10 g
- Toplam: 6 kutu
4. Sonuç Tablosu (Doldurulmuş Haliyle)
| Kütle | 10 g | 50 g | 100 g | 250 g | 500 g | 1 kg | 2 kg | 5 kg | 10 kg |
|---|---|---|---|---|---|---|---|---|---|
| 5 kg 200 g muz | 2 | 1 | |||||||
| 11 kg 500 g yağ | 1 | 1 | 1 | ||||||
| 285 g un | 3 | 1 | |||||||
| 325 g kimyon | 2 | 1 | 1 | ||||||
| 7 kg 375 g tavuk | 2 | 1 | 1 | 1 | 1 |
5. Kısa Özet
- Verilen ağırlıklar en büyükten küçüğe kutuları seçilerek ve eksik kalan kısımlar küçüklerle tamamlanarak bulunur.
- Bazı değerler kesin olmazsa, eksik kalan gramlar için tabloda olmayan kutuları ekleyemezsiniz. Bu durumda en yakın kutu kombinasyonları tercih edilir.
- Her madde için toplamda en az kutu seçilmiştir.
En Az Kutu Sayıları Tablosu
| Ürün | Seçilen Kutu Türleri | Kutu Toplamı |
|---|---|---|
| 5 kg 200 g muz | 1 × 5 kg, 2 × 100 g | 3 |
| 11 kg 500 g yağ | 1 × 10 kg, 1 × 1 kg, 1 × 500 g | 3 |
| 285 g un | 1 × 250 g, 3 × 10 g | 4 |
| 325 g kimyon | 1 × 250 g, 1 × 50 g, 2 × 10 g | 4 |
| 7 kg 375 g tavuk | 1 × 5 kg, 1 × 2 kg, 1 × 250 g, 1 × 100 g, 2 × 10 g | 6 |
Kısacası: Tabloyu yukardaki şekilde doldurabilirsin ve kutuların toplam sayısını her satırda en aza indirmiş olursun!