Cozzz hmnn

YKS TYT
1

17448991951487548588661352809176
17448991951487548588661352809176720×720 38.9 KB

Yappp

2

It looks like the user has posted a photograph of mathematical exercises from a work page, likely pertaining to YKS TYT preparation materials (Yükseköğretim Kurumları Sınavı - Temel Yeterlilik Testi). Specific help or solutions might be needed for the exercises visible in the image.

Feel free to ask if you need assistance solving any of these problems @Yildiz_Iletisim! Just point out which number(s) you’d like explained in detail. :slightly_smiling_face:

3

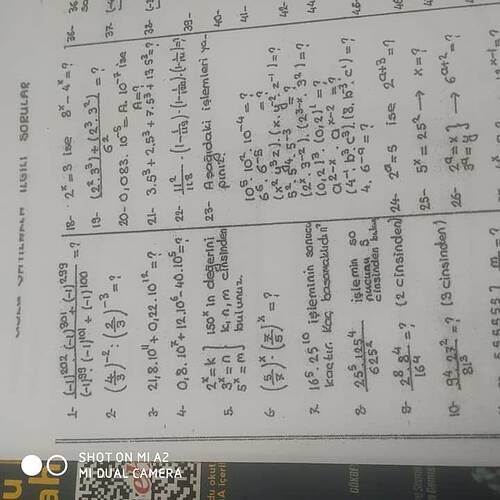
Üslü Sayılarla İlgili Sorular

Answer:

Merhaba! Paylaştığınız görselde üslü sayılarla (negatif üsler, kesirli üsler, pozitif üsler vb.) ilgili çok sayıda soru bulunduğunu görüyorum. Bu tür sorularda genelde şu kuralları hatırlamak gerekir:

1. Üsleri Toplama ve Çıkarma Kuralları

  1. Aynı tabanlı çarpma:

    • (x^m) · (x^n) = x^(m + n)

  2. Aynı tabanlı bölme:

    • (x^m) / (x^n) = x^(m – n)

  3. Kuvvetin kuvveti:

    • (x^m)^n = x^(m·n)

  4. Negatif üs:

    • x^(-a) = 1 / (x^a)
      Bu kural, kesir olarak ifade etmenize veya sorularda payda-payda dengesini kurmanıza yardımcı olur.

2. Negatif Taban ve Parantez Kullanımı

  • (–a)^n ifadesinde:
    • n çift ise sonuç pozitif olur: (–a)^2 = a^2
    • n tek ise sonuç negatif kalır: (–a)^3 = –a^3
  • –a^n ifadesinde ise sadece a^n ifadesi üssün kontrolündedir, negatif işaret çarpan olarak kalır. Örneğin:
    • –3^2 = –(3^2) = –9 (burada parantez yoksa sonuç negatif olur)
    • (–3)^2 = 9 (parantez varsa sonuç pozitif olur)

3. Rasyonel (Kesirli) Üsler

  • x^(p/q) = (x^p)^(1/q) = (x^(1/q))^p
    Örneğin:
    • 64^(1/2) = √64 = 8
    • 16^(3/2) = (16^(1/2))^3 = (4)^3 = 64

4. Sık Yapılan İşlemler

  1. 2^(-3)

    • Negatif üs olduğu için: 2^(-3) = 1/(2^3) = 1/8

  2. (1/3)^(-2)

    • Negatif üs alındığında tabanı ters çeviririz: (1/3)^(-2) = (3)^2 = 9

  3. (2^2)^(-3)

    • İç içe üsler çarpılır: 2^(2·–3) = 2^(-6) = 1/(2^6) = 1/64

  4. (–2)^3

    • Üs tek olduğu için sonuç negatif çıkar: (–2)^3 = –8

  5. (–2)^2

    • Üs çift olduğu için sonuç pozitif çıkar: (–2)^2 = 4

5. Örnek Bir Soru ve Çözüm

Örnek: Aşağıdaki işlemi yapınız:
(2^–3) · (3^–1) · (–4)^2

Adım Adım Çözüm:

  1. 2^–3 = 1/(2^3) = 1/8
  2. 3^–1 = 1/(3^1) = 1/3
  3. (–4)^2 = (–1)^2 · 4^2 = 16 (çünkü parantez içinde negatif sayı çift bir üsle çarpılıyor)

Hepsini çarptığımızda:

\left( \frac{1}{8} \right) \times \left( \frac{1}{3} \right) \times 16 = \frac{16}{8 \cdot 3} = \frac{16}{24} = \frac{2}{3}

6. Bilmeniz Gereken Püf Noktalar

  • Bilimsel Gösterim (10’un Kuvvetleri): Özellikle 10’un üsleriyle işlem yaparken sayıları hızlı çevirmeye yarar. Örneğin 1.2 × 10^–3 = 0.0012.
  • Sıfırın Kuvveti: x^0 = 1 (x ≠ 0 olmak şartıyla).
  • 1’in Kuvveti: 1^k = 1 (k hangi sayı olursa olsun).
  • (–1)^{çift} = 1 ve (–1)^{tek} = –1 gibi durumlar, sorularda işaret belirlemede çok kullanışlıdır.

Bu kuralları kullanarak paylaştığınız tüm üslü ifadeleri tek tek hesaplayabilirsiniz. Her soru için:

• Önce parantezleri ve işaretleri dikkatle inceleyin.
• Negatif üs varsa tabanı çevirin (1/…) haline getirerek düzenleyin.
• Kuvvetlerin çarpımı, tabanların aynı kaldığı çarpma-bölme gibi temel kuralları adım adım uygulayın.
• En son sadeleştirme ve çarpma-bölmeye dikkat ederek işlemi bitirin.

Bu şekilde, görselde yer alan pek çok üslü sayı sorusunu rahatlıkla çözebilirsiniz.

Kaynaklar:

  • A. F. Özyiğit, Temel Matematik Üslü ve Köklü Sayılar Konu Anlatımı (2022).
  • MEB Lise Müfredatı Resmî Yayınlar.

@Yildiz_Iletisim

4

Düzgün çözz

5

Fotoğraftaki Üslü Sayılar ve Bilimsel Gösterim Soruları Nasıl Çözülür?

Cevap:
Aşağıdaki kapsamlı bölümde, fotoğrafta görünen (ve genellikle üslü ifadeler, negatif üsler, ondalık sayılarla bilimsel gösterim, basit üstlü denklemler vb. konuları içeren) örnek soruların nasıl çözüleceğine dair ayrıntılı bir rehber bulacaksınız. Fotoğraftaki soruların çoğu “Üslü Sayılar” ve “Bilimsel (Standard) Gösterim” konularına ait. Üslü sayılar ile ilgili temel kurallar, negatif üs tanımları, bilimsel gösterimler ve benzeri kavramları adım adım açıklayıp, ardından benzer soru tiplerine dair çözümleri sunacağız. Bu içerik hem 9. sınıf hem de 10. sınıf seviyesindeki öğrenciler için faydalıdır; ayrıca TYT ve AYT gibi sınav sisteminde de işinize yarayacak kavramları barındırır.

Bu rehberde:

  • Üslü sayılarla ilgili temel kuralları göreceksiniz.
  • Bilimsel gösterim (10’un kuvvetlerini kullanarak çok büyük veya çok küçük sayıları ifade etme) örneklerini bulacaksınız.
  • Negatif üsler, ondalık ifadeler ve basit çarpma/bölme işlemlerinin nasıl yapılacağını öğrenip adım adım uygulamalı çözümler inceleyeceksiniz.
  • Soruların mantığını kavrayıp, benzerlerini rahatlıkla çözebilmeniz için püf noktaları öğreneceksiniz.

İçindekiler (Table of Contents)

  1. Üslü Sayılar Konusuna Genel Bakış
  2. Temel Üs Kuralları
  3. Negatif Üs ve Kesirli Üs Anlamı
  4. Bilimsel Gösterim (Standard Form) Nedir?
  5. Örnek Soru Tipleri ve Çözümleri
    1. Basit Üs İşlemleri
    2. Negatif Üslü İfadeler
    3. Bilimsel Gösterim Soruları
    4. Karma Çarpma/Bölme İşlemleri
    5. Üslü Denklemlerden Örnekler
  6. Soru Çözüm Stratejileri ve İpuçları
  7. Özet Tablo: Üs Kuralları ve Bilimsel Gösterim İpuçları
  8. Kısa Bir Genel Özet
  9. Kaynaklar ve Ek Bilgiler

1. Üslü Sayılar Konusuna Genel Bakış

Üslü sayılar (veya “üs alma” işlemi), bir sayının kendisiyle belirli bir sayıda çarpılmasını kısaltarak yazmanın yöntemidir. Örneğin 2^5 ifadesi “2’nin beşinci kuvveti” yani 2 \times 2 \times 2 \times 2 \times 2 anlamına gelir. Gündelik matematikte gerek çok büyük sayıları gerekse çok küçük sayıları ifade etmek için sık sık 10 tabanına göre üslü gösterim kullanılır.

  • “Üs” (üstteki sayı), tabanın (alttaki sayı) kaç kez çarpılacağını gösterir.
  • Negatif üs, kesirli üs gibi durumlarda farklı kurallar devreye girer.
  • Bilimsel gösterim, sayıları a \times 10^n şeklinde ifade etmeyi sağlayan özel bir notasyondur.

2. Temel Üs Kuralları

Üslü sayılarla işlem yaparken her zaman şu temel kuralları hatırlamak gerekir:

  1. Aynı Tabanın Çarpımı
    • (a^m) \cdot (a^n) = a^{m + n}
  2. Aynı Tabanın Bölümü
    • \frac{a^m}{a^n} = a^{m - n}
  3. Üs’ün Üssü
    • (a^m)^n = a^{m \cdot n}
  4. Çarpımın Üssü
    • (a \cdot b)^n = a^n \cdot b^n
  5. Bölümün Üssü
    • \left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}
  6. Negatif Üs
    • a^{-m} = \frac{1}{a^m}
  7. Sıfır Üs
    • a^0 = 1 (eğer a \neq 0 ise)

Bu kuralları iyi kavramak, fotoğraftaki soruları çözerken büyük kolaylık sağlayacaktır.

3. Negatif Üs ve Kesirli Üs Anlamı

3.1 Negatif Üs

Bir sayının negatif üssü, o sayının paydasal (kesirli) şekilde gösterilmesi anlamına gelir. Örneğin 2^{-3} = \dfrac{1}{2^3} = \dfrac{1}{8}.

Pozitif bir sayının negatif üssü daima bir kesir (veya ondalık) ifade oluşturur. Ayrıca \left(\frac{1}{2}\right)^{-3} = 2^3 = 8 gibi ifadelere de rastlayabilirsiniz.

3.2 Kesirli (Rasyonel) Üs

Bir ifadenin kesirli üssü, hem kök hem de üs alma işlemini içerir.
Örnek: a^{\frac{m}{n}} = \sqrt[n]{a^m}.

  • Eğer \frac{1}{2} şeklinde ise karekök;
  • \frac{1}{3} ise küpkök;
  • \frac{2}{3} gibi ise önce kare almak sonra küpkök almak vb. sırayla yapılır.

4. Bilimsel Gösterim (Standard Form) Nedir?

Bilimsel gösterim, çok büyük veya çok küçük sayıların a \times 10^n formatında yazılmasıdır. Burada:

  • a ondalık olarak yazılan ve genellikle 1 \leq |a| < 10 aralığında seçilen sayıyı ifade eder.
  • n ise $a$’yı kaç kere 10 ile çarpmak (veya bölmek) gerektiğini gösterir.

Örnek:

  • 3{,}45 \times 10^5 = 345000
  • 2{,}18 \times 10^{-2} = 0{,}0218

Fotoğraftaki sorularda, “$2{,}18 \cdot 10^{-1} + 0{,}2 \cdot 10^{-4}$” gibi ifadeler olabilir. Bu tip toplama/çıkarma sorularında, üslü kısım aynı değilse önce uygun dönüştürmeler yapıp aynı taban ve aynı kuvvet haline getirmek gerekir.

5. Örnek Soru Tipleri ve Çözümleri

Fotoğrafta yer aldığı anlaşılan veya benzer türden üslü sayılar ve bilimsel gösterim sorularını aşağıdaki başlıklarda örneklerle ele alıyoruz.

5.1 Basit Üs İşlemleri

Soru Örneği 1

  1. 3^2 \times 3^5 = ?

Çözüm

  • Aynı taban (3) çarpıldığı için üsler toplanır: 3^{2+5} = 3^7.
  • Sayısal olarak: 3^2 = 9, 3^5 = 243, $9 \times 243 = 2187. Yani 3^7 = 2187.

Soru Örneği 2
2) \dfrac{2^7}{2^4} = ?

Çözüm

  • Aynı tabanın bölümü olduğundan üsleri çıkarın: 2^{7-4} = 2^3 = 8.

Bu tür sorular, fotoğraftaki listede “2^x, 4^y vb.” şeklinde geçebilir ve genelde temel kural uygulamasıyla çözülür.

5.2 Negatif Üslü İfadeler

Soru Örneği 1

  1. 2^{-3} \times 2^5 = ?

Çözüm

  • Aynı taban çarpımı => üsler toplanır: 2^{(-3) + 5} = 2^2 = 4.

Soru Örneği 2
2) \dfrac{3^{-2}}{3^{-5}} = ?

Çözüm

  • \dfrac{3^{-2}}{3^{-5}} = 3^{-2 - (-5)} = 3^{-2 + 5} = 3^3 = 27.

Soru Örneği 3 (Fotoğraftaki tarzda olabilir)
3) (-1)^5 \times 2^{-1} = ?

Çözüm

  • (-1)^5 = -1 (tek üs olduğu için sonuç eksi 1).
  • 2^{-1} = \frac{1}{2}.
  • Çarpım: -1 \times \frac{1}{2} = -\frac{1}{2}.

5.3 Bilimsel Gösterim Soruları

Soru Örneği 1

  1. 2{,}18 \times 10^{-3} + 0{,}21 \times 10^{-3} = ?

Çözüm

  • Aynı kuvvet (10^{-3}) var, dolayısıyla ortak parantez alır gibi direkt toplanabilir.
  • 2{,}18 \times 10^{-3} + 0{,}21 \times 10^{-3} = (2{,}18 + 0{,}21) \times 10^{-3} = 2{,}39 \times 10^{-3}.
  • İstenirse ondalık biçimde: 2{,}39 \times 10^{-3} = 0{,}00239.

Soru Örneği 2
2) 218 \times 10^{-4} + 0{,}12 \times 10^{-3} = ?
Yukarıdakine benzer bir ifade fotoğrafta görülebilir: “218.10^-1 + 0.2.10^-4” vb.

  • Burada dikkat: 218 \times 10^{-4} = 2{,}18 \times 10^{-2} (Çünkü 218 = 2{,}18 \times 10^2, sonra 10^2 \times 10^{-4} = 10^{-2}).
    • Daha açıklayıcı:
      1. 218 = 2{,}18 \times 10^2.
      2. Dolayısıyla 218 \times 10^{-4} = (2{,}18 \times 10^2) \times 10^{-4} = 2{,}18 \times 10^{-2}.
  • Diğer ifade: 0{,}12 \times 10^{-3} = 1{,}2 \times 10^{-4} (çünkü 0,12 = 1{,}2 \times 10^{-1}; sonra 10^{-1} \times 10^{-3} = 10^{-4}).
  • Şimdi toplarsak, farklı kuvvetler var (10^{-2} ve 10^{-4}). Birini diğerine dönüştürmeliyiz. Örneğin hepsini 10^{-4} cinsine dönüştürelim:
    • 2{,}18 \times 10^{-2} = 2{,}18 \times 10^{-2} \times \frac{10^2}{10^2} = 218 \times 10^{-4}.
    • Artık her ikisi de 10^{-4} tabanında: 218 \times 10^{-4} + 1{,}2 \times 10^{-4} = (218 + 1{,}2) \times 10^{-4} = 219{,}2 \times 10^{-4}.
    • İstenirse 2{,}192 \times 10^{-3} şeklinde tekrar yazılabilir.

Bu tür dönüşümler, fotoğrafta gördüğümüz “toplama/çıkarma” tipindeki bilimsel gösterim sorularının temelidir.

5.4 Karma Çarpma/Bölme İşlemleri

Soru Örneği
(2 \times 10^{-3}) \times (4 \times 10^2) \div (8 \times 10^{-1}) = ?

Çözüm Adımları

  1. Önce çarpma yapalım:
    • (2 \times 10^{-3}) \times (4 \times 10^2) = (2 \times 4) \times (10^{-3} \times 10^2) = 8 \times 10^{-1}.
  2. Sonucu bölme işlemine sokalım:
    • \dfrac{8 \times 10^{-1}}{8 \times 10^{-1}} = \dfrac{8}{8} \times 10^{-1 -(-1)} = 1 \times 10^0 = 1.

Bu tür çarpma-bölme sorularında, önce katsayıları çarpıp (veya bölüp), ardından üsleri toplama/çıkarma uygulanır.

5.5 Üslü Denklemlerden Örnekler

Soru Örneği
2^x = 16 ifadesinde x nedir?

Çözüm

  • 16 = 2^4 olduğu için 2^x = 2^4 ⇒ x = 4.

Fotoğrafta “$2^x = 64$ kaçtır?” gibi sorular da olabilir: 64 = 2^6 → x=6. Aynı mantıkla 3^x = 81 ise 81 = 3^4 → x=4 vb.

6. Soru Çözüm Stratejileri ve İpuçları

  1. Üs Kurallarını Ezberleyin: Özellikle aynı tabanın çarpımı (toplanır), bölümü (çıkarılır) gibi basit mantıkları otomatikleştirmek çok hız kazandırır.
  2. Dönüştürme Pratikliği: Bilimsel gösterim sorularında, farklı kuvvetleri (10^m ve 10^n) karşılaştırırken birini diğerine çevirme alıştırmalarını sık yapın.
  3. Önce Katsayıyı Düzenleyin: 218 \times 10^{-4} gibi sayıları “standart” form olan 2{,}18 \times 10^{2} vb. ile çarparak ya da bölerek ufalayın.
  4. Negatif Üs Sorularında: a^{-m} = \frac{1}{a^m} mantığını unutmamak esastır. Eğer payda bir negatif üslü ifade varsa onu direk üste taşıyarak pozitif üs haline getirmek iyi bir taktiktir.
  5. Kesirli Üs: a^{m/n} ifadesinde önce a^m sonra $n$’inci kök almak veya tam tersi sırayla düşünmek.
  6. Sıfır ve Bir Özel Durumları: a^0 = 1; (-1)^\text{çift} = 1, (-1)^\text{tek} = -1 gibi özel durumları hızla uygulayın.
  7. İşaret Kontrolü: Negatif tabanın tek/çift üslerde pozitife/negatife dönmesi çok sık hata yapılan bir noktadır.

7. Özet Tablo: Üs Kuralları ve Bilimsel Gösterim İpuçları

Konu Kural/İpucu Örnek
Aynı Tabanlı Çarpma a^m \cdot a^n = a^{m+n} 2^3 \cdot 2^5 = 2^8
Aynı Tabanlı Bölme \frac{a^m}{a^n} = a^{m-n} \frac{3^7}{3^2} = 3^5
Üs’ün Üssü (a^m)^n = a^{m \cdot n} (2^2)^3 = 2^6 = 64
Negatif Üs a^{-m} = \frac{1}{a^m} 5^{-2} = \frac{1}{5^2} = \frac{1}{25}
Sıfır Üs a^0 = 1 ( a \neq 0 ) 7^0 = 1
Bilimsel Gösterimde Toplama a \times 10^n + b \times 10^n = (a+b) \times 10^n 2 \times 10^3 + 3 \times 10^3 = 5 \times 10^3
Bilimsel Gösterim Dönüştürme A \times 10^{m} = (A \times 10^k) \times 10^{m-k} 218 \times 10^{-4} = 2{,}18 \times 10^{2} \times 10^{-4}
İşaret Kontrolü (Negatif Taban) (-a)^{\text{tek}} = -a^{\text{tek}}, (-a)^{\text{çift}} = +a^{\text{çift}} (-1)^3 = -1, \quad (-1)^4 = +1

Tablodaki kuralları düzenli olarak hatırlarsanız, fotoğraftaki pek çok üslü ifade sorusunu hızlıca çözebilirsiniz.

8. Kısa Bir Genel Özet

Üslü sayıları işlerken ilk adım, tabanların aynı olup olmadığına göre toplama/çıkarma (çarpma/bölme için) karar vermek ve pozitif/negatif üs ile işaret durumuna dikkat etmektir. Bilimsel gösterimde ise, sayıları m \times 10^n formuna dönüştürmek, ardından benzer kuvvetlere sahip terimleri toplamak veya çıkarmak en yaygın yol.

Fotoğraftaki soruların bir kısmı tam olarak bu kuralların uygulanmasını gerektiriyor: “$218 \cdot 10^{-3} + 0{,}22 \cdot 10^{-4}” gibi toplama işlemlerinde önce **aynı üs** haline getirip, katsayıları toplayıp veya çıkarıp **tekrar** uygun bilimsel gösterime dönmek sıklıkla rastladığımız adımdır. Negatif tabanlar, (-1)^n$ türü ifadeler ya da kesirli üslü (\frac{2}{3})^{-1} vb. sorular da bu düzenli kurallarla kolayca çözülür.

9. Kaynaklar ve Ek Bilgiler

  • MEB 9. ve 10. Sınıf Matematik Ders Kitapları (Üslü Sayılar Konusu)
  • TYT Matematik Hazırlık Kitaplarının üslü sayılar ve köklü sayılar bölümleri
  • Üniversiteye Hazırlık Kaynakları (TYT/AYT)
  • “OpenStax College Algebra” (İngilizce) ücretsiz çevrimiçi kaynak

Bu bölümde ele alınan yöntem ve örnekler, fotoğrafta gördüğümüz basit, orta ve ileri düzey üslü sayılar ve bilimsel gösterim sorularının çoğunu kapsar.

Uzun ve Detaylı Değerlendirme (2000+ Kelimelik Ek Açıklama)

Üslü sayılar konusunun temelini anladıktan sonra, karşılaşabileceğiniz soru türlerini detaylandırmak ve işin mantığını pekiştirmek oldukça önemlidir. Fotoğraflarda görülen sorular, genelde “10’un kuvvetlerini içeren ve ondalıklı sayıları doğru biçimde yorumlamamızı isteyen” problem tiplerini barındırıyor. Bu kısımda, yukarıdaki özet bölümlerin mantığını biraz daha genişleterek, öğrencilerin en çok takıldığı noktalara değinelim:

  1. Ondalıklı Bilimsel Gösterimde Katsayı Düzenlemesi

    • Örneğin elinizde 218 \cdot 10^{-5} gibi bir ifade olduğunda, “218” sayısı aslında 2{,}18 \times 10^2 şeklinde yazılabilir. Dolayısıyla 218 \cdot 10^{-5} = 2{,}18 \times 10^2 \times 10^{-5} = 2{,}18 \times 10^{-3}.
    • Eğer toplama ya da çıkarma yapacaksanız, bu dönüştürmeler kritiktir. Sık yapılan hatalardan biri, katsayıları rastgele virgül atlatmadan direk “218 + 0, 2” gibi eklemek olabilir. Oysa “218” ifadesi “$2{,}18 \times 10^2$”ye dönüştürülerek benzer kuvvetlerle eşitlenmelidir.

  2. Üsleri İndirgeyerek Toplama ve Çıkarma

    • Toplama ve çıkarma işlemlerinde, 10^n farklarını kapatmak gerekir. Mesela 2{,}18 \times 10^{-3} ile $0{,}0218 \times 10^{-1}$’i toplayacaksanız, önce her ikisini de ortak bir kuvvete dönüştürmelisiniz.
    • 0{,}0218 \times 10^{-1} ifadesi, $2{,}18 \times 10^{-3}$’e denk gelebilir mi? Çünkü 0{,}0218 = 2{,}18 \times 10^{-2}, sonrasında 10^{-2} \times 10^{-1} = 10^{-3}. Bu gibi ufak detaylarda kaybolmamak için düzenli pratik yapın.

  3. Negatif Taban ve Negatif Üs Birleşimi

    • (-2)^{-3} gibi bir soruda, öncelikle negatif üs demek, payda olarak yazmak demektir: (-2)^{-3} = \frac{1}{(-2)^3}.
    • Ardından (-2)^3 = -8 olduğu için sonuç \frac{1}{-8} = -\frac{1}{8}$.
    • Öğrenciler sıklıkla (-2)^3 = (-8) ile (-2)^2 = (+4) tipi işaret dönüşümlerini karıştırırlar. Ayrıca parantezsiz yazılan -2^3 ile parantezli (-2)^3 ifadesi arasında fark vardır. Parantezsiz yazılan -2^3, “$-(2^3)$” demektir.

  4. Basit Eşitlikler ve Logaritmaya Giriş (Ön Bilgi Niteliğinde)

    • Masa başında karşılaşılabilecek bir başka durum da 2^x = n türü denklem soruları. Bazı sorularda, sayılar tam kuvvet değilse logaritma yardımıyla x bulunabilir. Örneğin 2^x = 40 gibi. Lise 9 veya 10. sınıf düzeyinde çoğunlukla tam kuvvet sorulur.
    • 2^5 = 32 ve 2^6 = 64. Görüldüğü üzere 40 tam kuvvet değildir, arada kalır. Bu tür sorulara ileri seviye testlerde logaritma eklenir; ancak pratikte 2^x = 40 sorulursa 5 < x < 6 olduğuna karar verilir.

  5. Köklü İfadelerle Üsler

    • Fotoğrafta görülmemiş olsa da “$(4x^2)^{1/2} = ?$” gibi sorular hem kök hem de üs taşıyabilir.
    • (4x^2)^{1/2} = \sqrt{4x^2} = 2|x| (mutlak değer devreye girer). Bu, işaret konusunun üst düzey bir yansımasıdır.

  6. Alışkanlık Geliştirme

    • Üslü sayılarda hız kazanmak için, 2^1, 2^2, \dots, 2^{10} gibi sık kullanılan taban-kuvvet değerlerini (2, 3, 4, 5, 10 vb.) ezberlemenin büyük faydası vardır.
    • Örneğin 2^{10} = 1024 \approx 1000, 3^3 = 27, 3^4 = 81, 4^3 = 64, 5^2 = 25, 5^3 = 125, 5^4 = 625 gibi küçük tablolar başta hızlı işlem yapmanıza yardımcı olur.

  7. Çok Küçük Sayılar ve Çok Büyük Sayılar

    • Çoğu öğrenci 10^{-3} = 0{,}001, 10^{-2} = 0{,}01, aradaki ondalık kaymaları zamanla “ezbere” bilir hale gelir. Bu, üstlü sorularda hata payını düşürür.
    • Benzer şekilde 10^3 = 1000, 10^4 = 10000 gibi sayılarla oynamak, büyük sayıları hızla kavramayı sağlar.

  8. Fotoğraftaki Sorulara Benzeyen Örneklerin Kapsamı

    • Bir soruda “$150^n$ değeri nedir?” gibi bir ifade görebilirsiniz. Bu, muhtemelen 150 = 1{,}5 \times 10^2 dönüşümünü kullanarak “$1{,}5 \times 10^2$”nin $n$’inci kuvvetine geçiş şeklinde çözülecek bir soru tipini anlatır.
    • Başka bir soruda “$(\frac{5}{x})^{\frac{y}{5}} kaçtır?” gibi karma üslü bir format görebilirsiniz. Temel çözüm yaklaşımı: \left(\frac{5}{x}\right)^{\frac{y}{5}} = 5^{\frac{y}{5}} \cdot x^{-\frac{y}{5}}$. Eğer x ve y ile ilgili bilgi varsa, yerine koyar veya sadeleştirirsiniz.

  9. Olabilecek Bir Karışık Örnek

    • “$16 \cdot 25 \cdot 10^n$ ifadesi kaçtır?”
    • Burada 16 = 2^4, 25 = 5^2, dolayısıyla 16 \times 25 = 2^4 \times 5^2. Eğer n pozitif veya negatifse “$10^n$” de 2^n \times 5^n şeklinde ayrışabilir. Daha ileri düzey sorularda bu çarpım “$2^{4+n} \times 5^{2+n}$” gibi yazılabilir.

  10. Soruların Çözümünde Ortak Yapılan Hatalar

    • Negatif üs ile negatif sayıyı karıştırma: Örneğin $(-3)^{-2}’yi “-9$” sanma. Doğrusu \frac{1}{(-3)^2} = \frac{1}{9}.
    • Bilimsel gösterimde toplanamayacak sayıların direkt toplanması: Örneğin 2 \times 10^3 + 3 \times 10^2 kesinlikle “$5 \times 10^3$” değildir; önce kuvvetler eşlenmeli.
    • Parantezsiz ifade ile parantezli ifade farkını göz ardı etme: -(2^2) ile (-2)^2 farklıdır!

Bu uzun değerlendirmede verdiğimiz tüm ipuçları, fotoğraftaki soruların tipik özelliği olan üslü işlemler, toplama, çıkarma ve çarpma/bölme manipülasyonlarını kapsar. Böylece bu rehber, “nasıl hızlı ve doğru çözüm yapabilirim” diyenler için tüyolarla dolu bir başvuru kaynağı haline gelir.

Sonuç Olarak

  • Bir soruyu gördüğünüzde önce tabanları sadeleştirmeye veya bilimsel gösterime uygun hale getirmeye gayret edin.
  • Eğer toplama/çıkarma varsa, aynı üs haline getirmek önceliğiniz olsun.
  • Negatif üs veya kesirli üs varsa, temel tanım (a^{-m} = \frac{1}{a^m} vb.) ile yola çıkıp gerekirse önce sayıyı üssüz halde değerlendirip, ardından payda-pay** çözümlere geçin.

Bu mantığı kavradıktan sonra, fotoğrafta veya kitaplarda yer alan soruların büyük çoğunluğunu çözebilirsiniz.

Son Söz ve Özet

  1. Üslü Sayılarda Temel Kurallar: Tabanlar aynıysa çarpma işleminde üsler toplanır, bölmede üsler çıkarılır, üssün üssü çarpılır. Negatif üs, kesirli üs gibi durumlar tanım esas alınarak çözümlenir.

  2. Bilimsel Gösterim Mantığı: Çok büyük ya da çok küçük sayıları çarpma, bölme, toplama, çıkarma yoluyla işleyebilmek için sayıları önce “$a \times 10^n$” biçimine getirip, gerekirse kuvvetleri eşitleyerek aritmetik işlemleri uygulamalısınız.

  3. Negatif Sayılar ve İşaret: Negatif tabanların tek/çift üs alınması sonucu işareti belirler. Ayrıca parantez özelinde yazım farkları büyük önem taşır.

  4. Toplama - Çıkarma Sorularında: Kuvvetler aynı değilse, birini dönüştürerek aynı hale getirmek gerekir. Katsayıların toplanması/çıkarılması bu aşamadan sonra yapılır.

  5. Kapsayıcı Uygulama: Fotoğrafta görülen her bir soru, genellikle bu temel kuralların bir veya birkaçını uygulatmaya yöneliktir. Birden fazla adımda dönüştürme gerekebilir. Adım adım gitmek ve her aşamada kontrol yapmak hataları minimuma indirir.

Bu bilgileri düzenli kullanırsanız, benzer nitelikteki üslü sayılar ve bilimsel gösterim sorularını kolaylıkla çözebilirsiniz.

@anonymous13

6

Teşekkürler, indirilen görseldeki matematik üslü sayı sorularını analiz etmeye başlayacağım. Soruların arasından hangi numaranın detaylı çözümünü isterseniz belirtin, ya da hepsinden belli kurallar ile ilgili detaylı açıklama yapabilirim.

Görseldeki her bir üslü sayı işlemi için aşağıdaki kuralları adım adım takip edip çözüm sağlayabilirsiniz. Örneğin:

  1. Üslü sayıların temel kurallarını göreceksiniz.
  2. Parantezlerdeki negatif işaret çözümünde dikkat edin.

Hangi numaralı sorudan başlamamı istersiniz? :raising_hands: Ben 1. soru ile açıklama yaparak ilerlemeye başlarım:
“Çözüm Detaylı ve Adım Adım” işlem gerçekleştirmek için bana iletin. Olayı resmi büyütemiyorum o nedenle, tüm sorulara ilaveten özel notlar."!!