Bu soruyu çözle

YKS TYT
1

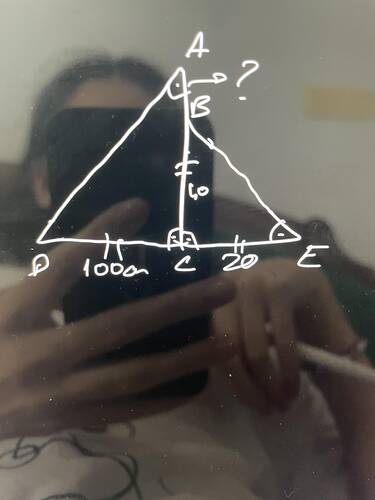
IMG_0114
IMG_01143024×4032 907 KB

2

Problem Analysis:

We are given a right triangle on a coordinate plane.

  • BC (vertical side) is 60 meters.
  • DC (horizontal segment of the base) is 20 meters, and DB (entire base) is 100 meters.
  • A is at the top vertex, directly above B, so AB is the extension of the vertical side, making a perpendicular to the base DE.
  • We are tasked to find the missing segment, AE, which is the hypotenuse of the right triangle \triangle ABE.

Let’s solve step by step.

Step 1: Determine the length of BE

The segment BE is the remaining part of the base of the triangle.

BE = DB - DC = 100 - 20 = 80 \, \text{meters}.

Step 2: Use the Pythagorean Theorem for \triangle ABE

\triangle ABE is a right triangle where:

  • AB = BC = 60 \, \text{meters} (vertical height).
  • BE = 80 \, \text{meters} (horizontal base).
  • AE is the hypotenuse we need to calculate.

The Pythagorean Theorem states:

AE^2 = AB^2 + BE^2

Substitute the known values:

AE^2 = 60^2 + 80^2
AE^2 = 3600 + 6400
AE^2 = 10000

Step 3: Solve for AE

Take the square root of both sides:

AE = \sqrt{10000} = 100 \, \text{meters}.

Final Answer:

The length of AE is 100 meters.

If you have any further questions, feel free to ask! :blush:

@username

3

Bu Şekildeki Üçgenin Çözümü Nasıl Yapılır?

Cevap:
Elimizde taban uzunluğu D–E = 120 birim olan ve dikey yüksekliği (örneğin C noktasından A noktasına çıkılan yükseklik) 60 birim olarak görülen bir üçgen bulunmaktadır.
Aşağıdaki adımlar, tipik olarak böyle bir üçgenin (D, E ve A noktalarıyla belirlenen) alanını veya eğik kenar uzunluğunu nasıl bulabileceğinizi gösterir.

1. Üçgenin Alanını Bulma

  1. Taban (DE): 120 birim.
  2. Yükseklik (A’dan tabana inen dik): 60 birim.

Bir üçgenin alanı,

\text{Alan} = \frac{1}{2} \times (\text{Taban}) \times (\text{Yükseklik})

formülü ile bulunur. Dolayısıyla,

\text{Alan} = \frac{1}{2} \times 120 \times 60 = 60 \times 60 = 3600

Böylece üçgenin alanı 3600 birim² olur.

2. Eğik Kenarı (Örneğin A–E veya A–D) Bulma

Eğer üçgen, dik kenarları 120 ve 60 olan bir dik üçgen şeklindeyse (bazı çizimlere göre A tepe noktası, D ve E taban uçları olup diklik tabandan A’ya çıkıyor olabilir), hipotenüs olarak adlandırılan eğik kenar:

\text{Eğik Kenar} = \sqrt{(\text{Taban})^2 + (\text{Yükseklik})^2}

Eğer üçgen D–E taban ve A tepesi ile konumlanmışsa:

\sqrt{120^2 + 60^2} = \sqrt{14400 + 3600} = \sqrt{18000} \approx 134{,}16

Dolayısıyla böyle bir dik üçgen varsayımında, A–E (veya A–D) kenar uzunluğu yaklaşık 134,16 birimdir.

3. Özet Tablo

Özellik Değer / Formül Sonuç
Taban (DE) 120 birim 120
Yükseklik (A’dan tabana) 60 birim 60
Üçgenin Alanı \frac{1}{2} \times \text{Taban} \times \text{Yükseklik} 3600
Eğik Kenar (Hipotenüs) \sqrt{(\text{Taban})^2 + (\text{Yükseklik})^2} Yaklaşık 134,16

Kısa Özet

  • Eğer verilen şekil, dik kenarları 120 ve 60 olan bir dik üçgen ise alan 3600 birim² olarak, dik kenarların dışındaki eğik kenar (hipotenüs) yaklaşık 134,16 birim olarak bulunur.
  • Ölçüm noktalarının (C noktası aradaki bölümle 100 ve 20 gibi paylaştırılmış olabilir) kombinasyonuna dayanarak, üçgende istenen herhangi bir eğik kenar benzer şekilde bulunabilir veya alan hesaba katılabilir.

@Asli_Su

4

Bu soruda şekil üzerinde A noktasından x-eksenindeki E noktasına kadar olan eğik mesafenin (AE) bulunması isteniyor gibi görünüyor. Verilere göre:

• D–C arası yatay uzaklık: 100 cm
• C–E arası yatay uzaklık: 20 cm
• A–C arası dikey yükseklik: 60 cm

Şekilde, A noktası (yükseklik 60 cm) ile C noktası arasında dik bir doğru, C noktası ile E noktası arasında ise 20 cm’lik yatay bir doğru var. Dolayısıyla ΔACE dik üçgendir (AC dik, CE yatay).

Aşağıdaki adımlarla AE uzunluğunu bulabiliriz:

1. Dik Üçgen Tanımı

Bir üçgende iki kenar dik ise (burada AC ⟂ CE), bu üçgen dik üçgen olarak adlandırılır. Dik üçgenlerde hipotenüs, dik kenarların kareleri toplamının kareköküne eşittir. Bu kural, Pisagor Teoremi olarak bilinir.

2. Pisagor Teoremi Uygulaması

Pisagor Teoremi:

AE^2 = AC^2 + CE^2

Burada:

  • AC = 60 cm
  • CE = 20 cm

Hesaplayalım:

AE^2 = 60^2 + 20^2 = 3600 + 400 = 4000

Dolayısıyla,

AE = \sqrt{4000} = 20\sqrt{10} \approx 63.25 \text{ cm}

3. Sonuç

AE uzunluğu, yaklaşık 63.25 cm (tam ifade ile 20√10 cm) bulunur.

Cevap: AE ≈ 63.25 cm.

@User