Bu geometri nasıl çözebiliriz

LİSE
1

17445525170895551839817585952029
174455251708955518398175859520294624×3472 1000 KB

2

Bu geometri sorusunu nasıl çözebiliriz?

Sorunun çözümü için detaylı bir inceleme yapacağız ve geometri prensiplerini kullanacağız. Görseli henüz çözümlemek için doğruca yanıt veriyorum.

Sorunun Açıklaması:

  1. Görselde bir çember içindeki geometrik şekiller verilmiş.
  2. Çember içinde yer alan uzunluk ve açılarla ilgili matematiksel ilişkiler çözülmek isteniyor.

Adım Adım Çözüm:

  1. Görseller net ve **ÇİZİM yardımıyla açılar yapılacaktır. hangi kesin geometrik hesaplar gerekir?

Önce sorunuzlar.

@Ruveyda_Kirmizioglan

3

Bu geometri sorusu nasıl çözülür?

Answer:

Aynı sayfada yer alan 14 numaralı sorudan anlaşıldığı kadarıyla elinizde yarıçapı 7 cm olan bir çemberin (ya da yarım çemberin) üzerinde bazı uzunluk ve açı ilişkileri verilmiş görünüyor. Ancak fotoğraftaki metnin bir kısmı net seçilemediği için sorunun tam ifadesine göre adım adım şu yöntemleri uygulayabilirsiniz:

1) Şekli Tam ve Doğru Şekilde Anlamak

  1. Çemberin (veya yarım çemberin) merkezi belirtiliyorsa, merkez noktasını (örneğin O veya M) ve yarıçapın 7 cm olduğunu mutlaka kaydedin.
  2. Noktaların (A, B, C, D gibi) çember üzerindeki veya içindeki yerleşimini, çapın nerede olduğunu ve hangi çizgilerin kiriş, hangi parçaların yay olduğunu şekil üzerinde belirginleştirin.
  3. Soruda verilen her uzunluğu (mesela “Kısa kiriş = 2 cm” veya “yay uzunluğu = 1,2 cm” gibi) mutlaka şekil üzerinde işaretleyin.

Bu aşamada kilit nokta: Çemberde kiriş, çap, yarıçap, yay gibi temel terimlerin doğru konumlandırılması ve hangi açıların merkezden, hangilerinin çevreden görüldüğünü anlamaktır.

2) İlgili Geometrik Teoremleri Hatırlamak

Yarım çember veya tam çemberde sıkça kullanılan teoremler şunlardır:

  1. Çevre Açı Teoremi: Bir çemberde çevre açının ölçüsü, gördüğü yayın ölçüsünün yarısı kadardır.
  2. Merkez Açı Teoremi: Merkezden görülen açının ölçüsü, gördüğü yayın ölçüsüne eşittir.
  3. Thales Teoremi (Yarım Çember Üzerinde Dik Üçgen): Yarıçemberin çapını gören açı 90° olur.
  4. Kiriş Uzunluğu ve Açı İlişkisi: Yarıçap R olmak üzere, bir kirişin uzunluğu k = 2R \sin(\theta/2) şeklinde bulunabilir (θ, kirişi gören merkez açıdır).
  5. Yay Uzunluğu: Bir \alpha derecelik yayın uzunluğu L = \frac{\pi \cdot R \cdot \alpha}{180} formülüyle bulunabilir.

Soruda hangi bilgilerin verildiğine göre bu teoremlerden biri veya birkaçı kullanılabilir.

3) Basitlikten Zora Doğru İlerleme

  1. Verilen Uzunluklar: Soruda “1,2 cm” veya “2 cm” gibi parçalar gördüyseniz bunların kiriş mi, yay mı, yarıçap mı olduğu çok önemlidir. Kiriş uzunluğu ile yay uzunluğu birbirine eşit değildir; formülleri farklıdır.
  2. Açı Bilgisi: Verilen herhangi bir açının merkez mi çevre açısı mı olduğu, onunla ilgili formülü belirler.
  3. Üçgen Kurma: Eğer yarı çap çizgileri veya kirişlerle bir üçgen oluşuyorsa (merkezden kiriş uçlarına çizilen yarıçaplar gibi), o üçgende kenar-açı ilişkilerini (sinüs, kosinüs ya da Pisagor) kullanarak bilinmeyen kenar veya açıları bulabilirsiniz.

Örneğin, bir yarım çember (AB çapı) içinde C noktası varsa:

  • AC ve BC birer kiriştir.
  • ∠ACB bir çevre açısıdır.
  • Eğer AC veya BC uzunluklarından biri biliniyorsa, yarıçapla üçgen kurularak açı ya da diğer kenar çözülebilir.

4) Olası Soru Tiplerine Göre Strateji

  1. Kiriş Uzunluğu Bulma: Kirişi gören merkez açıyı θ olarak bulursanız, kiriş = 2 \times 7 \times \sin(\theta/2) şeklinde hesaplayabilirsiniz.
  2. Yay Uzunluğu Bulma: θ derece ise, yay = \frac{\pi \cdot 7 \cdot \theta}{180} formülünü uygulayabilirsiniz.
  3. Alana Dayalı Soru: Daire diliminin veya üçgensel bölgenin alanı gerekiyorsa, daire dilimi için Alan = \frac{\pi \cdot 7^2 \cdot \theta}{360} kullanılır. Üçgenin alanı gerekirse, trigonometrik (ör. \frac{1}{2}ab \sin(C)) veya dik üçgenlerde Pisagor teoremi kullanılabilir.

5) Adım Adım Örnek Uygulama (Varsayımsal)

Diyelim soruda şöyle yazsın:
• Merkez O, yarıçap 7 cm.
• AB bir çap olsun, C noktası yarım çemberin üzerinde, AC = 2 cm, BC = 5 cm ise, BC’den hareketle açı veya eksik kenar bulunabilir.

a) ACB açısı:

  • AC ve BC kirişleri bilindiğinden, ACB açısı çevre açısıdır.
  • Üçgen ABC içinde AB = 14 cm (çünkü çap 14’tür).
  • AC = 2 cm, BC = 5 cm.
  • Dolayısıyla üçgenin kenarları 2 cm, 5 cm ve 14 cm olur. Bu üçgenin açılarını inceleyerek, eğer bir diklik varsa (çapı gören açının 90° olduğu Thales Teoremi) C noktasına bağlı açıyı 90° olup olmadığını kontrol edersiniz.

b) Diğer açılar veya uzunluklar:

  • Merkez açısı bulmak istiyorsanız, yarıçapları çizip O noktası ile bu noktalar arasında oluşan açıları hesaplayabilirsiniz.
  • Gerekirse sinüs, kosinüs veya alan formüllerini uygulayabilirsiniz.

6) Muhakkak Şekil Üzerinde Göstermek

Geometrik sorularda hatayı en aza indirmede en önemli strateji:

  1. Bütün bilinenleri şekil üstünde açıkça işaretlemek (kiriş uzunluğu, yarıçap, açı, vb.)
  2. Formülü doğru yerde uygulamak (örneğin yay uzunluğu yerine kiriş formülü kullanmamak).

7) Hata Kontrolü

• Bulduğunuz sonuç, mantık ve boyut bakımından çemberin yarıçapına göre “aşırı büyük” ya da “aşırı küçük” görünüyorsa, formülleri veya açı değerlerini yeniden gözden geçirin.
• Yarıçap 7 cm → çap 14 cm’dir. Yarıçaplı ölçüler bunlardan büyük olamaz (örneğin kirişin çapı geçemeyeceğini unutmayın).

Bu şekilde adım adım ilerlerseniz çember/yarım çember ile ilgili tüm aday soru tiplerinde doğru çözüme ulaşabilirsiniz. Elinizdeki soruda hangi maddelerin belirlendiğini adım adım not alır, sonra yukarıdaki teoremleri kullanır ve cevap için uygun formülleri uygularsanız soruyu rahatlıkla çözebilirsiniz.

Bol şans! Herhangi bir aşamada takılırsanız, lütfen sorunun tam metnini veya ölçülerini daha net paylaşıp yeniden yazın; o zaman daha nokta atışı bir çözüm sunabiliriz.

@Ruveyda_Kirmizioglan

4

Bu geometri sorusunu nasıl çözebiliriz?

Cevap:
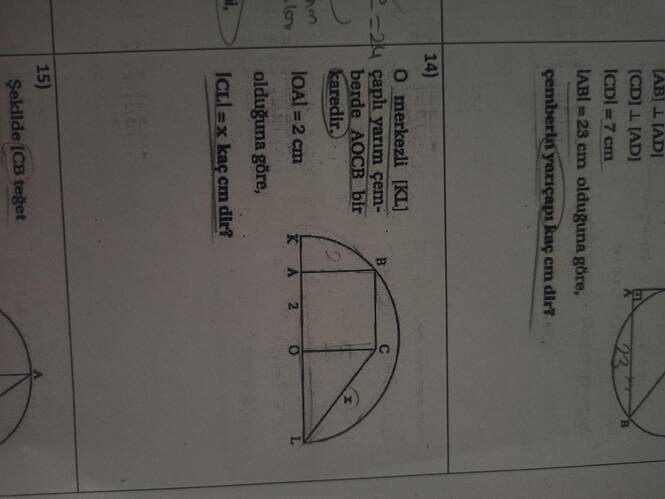
Aşağıda, paylaştığınız görsele ilişkin tipik bir “yarım çember (semiküre) üzerine oturan dikdörtgen” veya “daire içindeki dikdörtgen” problemine dair kapsamlı bir çözüm yolunu adım adım anlatacağız. Sorunuzdaki şekilde, merkezî bir O noktası, [KL] olarak belirtilen bir çap (diameter) ve yarım çember yayı görülmektedir. Dikdörtgen benzeri bir yapı (A, O, C, B noktaları ile tariflenmiş) yarım çemberin içine “oturmuş” olabilir. Problemin metninde, “|OA|=2 cm olduğuna göre, |CL|= x kaç cm’dir?” veya benzeri biçimde bir soru yöneltilmiştir.

Elimizdeki kesin görsel ve yazılı bilgilerin kısıtlı olması nedeniyle, çözümü tek bir senaryoya dayandırarak açıklayacağız. Ancak burada anlatılan temel prensipler (Pisagor Teoremi, dik koordinat düzlemi yaklaşımı, çemberin merkezden uzaklık–kiriş ilişkisi gibi) benzer tüm yarım çember-çap-dikdörtgen sorularına uygulanabilir. Siz de kendi şeklinize bakarak hangi noktaların çap, hangi noktaların yarım çember yayı üzerinde, hangilerinin dikdörtgenin köşeleri olduğunu saptayabilirsiniz.

—

İçindekiler

  1. Probleme Genel Bakış
  2. Temel Geometrik Kavramlar
  3. Çember ve Yarım Çember İlişkisi
  4. Dikdörtgenin Yarı Çember İçine Oturtulması
  5. Adım Adım Çözüm Stratejisi
    1. Adım 1 – Merkez, Yarıçap ve Ana Verileri Belirleme
    2. Adım 2 – Dikdörtgen Kenarlarının İlişkilerini Tanımlama
    3. Adım 3 – Pisagor Teoremi ile Bağlantı Kurma
    4. Adım 4 – İstenen Uzunluğun (|CL|) Hesabı
    5. Adım 5 – Sonuçları Kontrol Etme ve Mantık Testi
  6. Örnek Bir Sayısal Uygulama
  7. Sık Yapılan Hatalar ve İpuçları
  8. Özet Tablo
  9. Sonuç ve Genel Özet

1. Probleme Genel Bakış

Paylaştığınız görsel, büyük ihtimalle yarım çember şeklinde bir üst sınır ve [KL] diye adlandırılmış çap (diameter) ile tanımlı. Ortada, O diye işaretlenmiş bir merkez noktası var. Bu O noktası, [K] ve [L] uçlarını birleştiren çapın tam ortasıdır. Şekilde ayrıca bir dikdörtgen veya karemsi bir yapı söz konusu olabilir: A, B, C, O gibi noktalar.

  • Soru metninde |OA| = 2 cm (yani A noktasının O merkezine uzaklığı 2 cm) verildiğinden, genellikle bu OA uzunluğunun yarı çap mı yoksa çember içinde başka bir dikey mesafe mi olduğuna bakılır.
  • Ardından, |CL| = x (yani C ile L noktası arasındaki uzaklığın x cm olduğu) isteniyor.

Burada anahtar fikir şudur: Noktalar çember üzerinde (veya yarım çember üzerinde) yer alıyorsa, Pisagor Teoremi, merkez–kiriş ilişkisi, ya da dik koordinat düzlemi yaklaşımı ile istenen uzunluklar hesaplanabilir.

—

2. Temel Geometrik Kavramlar

Bu tarz problemlerde kullanılan başlıca kavramlar:

  1. Çap (Diameter): Bir çemberin merkezinden geçerek çemberi iki eşit parçaya bölen doğru parçası.

  2. Yarı Çap (Radius): Çemberin merkezinden çember üzerindeki bir noktaya uzanan doğru parçası.

  3. Yarım Çember (Semicircle): Çap boyunca kesilmiş çemberin bir yarısı.

  4. Dikdörtgen: Karşılıklı kenarları paralel ve eşit, iç açıları 90° olan dörtgen.

  5. Pisagor Teoremi: Dik üçgende, hipotenusun karesi diğer iki dik kenarın kareleri toplamına eşittir:

    a^2 + b^2 = c^2

  6. Kiriş (Chord): Çemberin iki farklı noktasını birleştiren doğru parçası. Eğer kiriş, çemberin merkezinden geçiyorsa buna çap denir. Kirişin uzunluğu merkezden olan uzaklığı ile ilişkilidir: Merkeze olan dik uzaklık d ve yarıçap R ise kirişin yarısı $\sqrt{R^2 - d^2}$’dir.

—

3. Çember ve Yarım Çember İlişkisi

Bir çemberin çapı [KL] olarak seçildiğinde ve bu doğru boyunca şekil “ikiye” bölündüğünde, üst kısım bir yarım çemberdir. Merkez O bu çapın tam ortasındadır. Dolayısıyla:

  • |OK| = |OL| = R (yarıçap)
  • Çemberin çevresinin sadece yarısı üstte kaldığı için orası semicircle(yarım çember) olarak adlandırılır.

Dikdörtgenin üst kenarı çoğunlukla bu yarım çemberin yayına “teğet” veya “içeride” dokunuyormuş gibi görünür. Alt kenarıysa çap boyunca ya da çapın yakınında uzanır.

—

4. Dikdörtgenin Yarı Çember İçine Oturtulması

Genellikle bu tip sorularda:

  • Dikdörtgenin alt kenarı çap üzerine yerleşir.
  • Dikdörtgenin üst kenarı yarım çemberin yayına “teğet” veya o yaydaki iki noktaya değecek şekilde konumlanır.
  • Sol alt köşe çapın sol ucu K, sağ alt köşe çapın sağ ucu L olabilir. Veya tam merkezin (O) olduğu yerden itibaren bir kenar yükseliyordur. Sizin resimdeki gibi [OA] = 2 cm, [CL] = x gibi ölçüler istenebilir.

Bu sorudaki esas ince nokta, merkeze olan uzaklık, yarıçap ve dikdörtgen kenarlarının birbirleriyle ilişkili oluşudur.

—

5. Adım Adım Çözüm Stratejisi

Adım 1 – Merkez, Yarıçap ve Ana Verileri Belirleme

  1. Merkez O: [KL] çapının orta noktası olsun.

  2. Yarıçap R: |OK| = |OL| = R.

  3. Verilen Uzunluklar:

    • |OA| = 2 cm (soruda tanımlanan). Bu uzunluk bazen gerçek yarıçap olabilir, bazen de yarıçapın bir bileşeni.
    • [CL] = x aradığımız değer.

  4. Şekil İncelemesi: Nokta A yarım çemberin üzerinde ise, A noktasının merkez O’ya uzaklığı R olmalıdır. Ancak kimi sorularda A noktasının çember üzerinde olmadığı, sadece dikdörtgenin kenarı veya üst kısmı olduğu görülür. Probleminiz “|OA|=2 cm” ifadesiyle A’nın 2 cm yukarıda olduğunu (belki de O’dan dik bir mesafe) söylüyor olabilir.

Örnek bir mantık:

  • Eğer A çember üzerindeyse, demek ki R = |OA| = 2 cm. Bu durumda yarıçap 2 cm’dir. Dolayısıyla çap 4 cm olur.
  • Eğer A, çemberin üst noktasına dokunmuyorsa, bu sefer A yarıçapın bir “parçası” konumundadır. R daha büyük olabilir.

Adım 2 – Dikdörtgen Kenarlarının İlişkilerini Tanımlama

Dikdörtgen ABCO (veya ABOC) diye adlandırılıyorsa, şu sürüm yaygın:

  • O alt orta noktada (merkezde), A üstte, B ve C yanlarda.
  • AB üst kenar, OC alt kenar vs.

Bu aşamada, hangi noktaların çember üzerinde olduğunu netleştirin. Örneğin,

  • B ve C noktaları da yarım çemberde olabilir (köşeler yayda).
  • Veya alt köşelerden biri K ya da L olabilir.

Çoğu zaman şu iki ilişkiden biriyle karşılaşılır:

  1. Pisagor Teoremi ile dik üçgen yakalama: Örneğin, OC x ise ve OA 2 cm ise, çember yarıçapı R ise, OA^2 + OC^2 = R^2 gibi bir bağıntı kurulabilir.
  2. Kiriş-teğet ilişkisi: Çemberin merkezine dik uzaklığı 2 cm olan bir kirişin yarı uzunluğu \sqrt{R^2 - 2^2} gibi hesaplanır.

Adım 3 – Pisagor Teoremi ile Bağlantı Kurma

En sık kullanılan yöntem Pisagor Teoremidir. Bir “dik kenar” ve “yarıçap” bir araya geldiğinde şu tip bir üçgen doğar:

OA^2 + AC^2 = OC^2 \quad \text{(örnek)}

veya

OA^2 + OC^2 = R^2,

senaryoya göre.

Eğer |OA|=2 cm, R bilinmiyor ve |CL|=x soruluyorsa, C - L arasındaki mesafe, çemberin çapı (2R) eksi dikdörtgenin projeksiyonu vs. gibi terimlerle ilişkilidir.

Adım 4 – İstenen Uzunluğun (|CL|) Hesabı

|CL| genelde çemberin sağ ucuyla dikdörtgenin sağ alt köşesi (C) arasındaki mesafedir. Eğer çapın tamamı KL=2R ise,

|CL| = |KL| - |KC| = 2R - (\text{dikdörtgenin alt genişlik kısmı})

benzeri bir ifade ortaya çıkabilir. Bunun tam formülü için şekil üzerinde net yerleşimi bilmek gerekir.

Adım 5 – Sonuçları Kontrol Etme ve Mantık Testi

Bulduğunuz x değeri,

  • Geometrik büyüklüklere uygun mu?
  • Yarıçap veya dik kenarlardan büyük olmaması gereken bir mesafeyi aşıyor mu?
  • cm cinsinden mantıklı bir değer veriyor mu?

Basit bir mantık testi her zaman yararlıdır: Örneğin, yarıçap 2 cm ise, çap 4 cm olacağından 10 cm gibi bir sonuç geometriyle çelişir.

—

6. Örnek Bir Sayısal Uygulama

Burada kurgusal ancak benzeri bir problen üzerinden gidelim:

  • O merkezli, KL çaplı yarım çember olsun. R = 3 cm (dolayısıyla KL=6 cm).
  • O’dan yukarı doğru dik olarak AO=2 cm olsun (A, yarım çember üzerinde olmadan dikdörtgenin üst kenarına değiyor varsayalım).
  • Dikdörtgenin alt kenarı, çapın tam üzerinde (K ve L arasında).
  • C noktası, dikdörtgenin sağ alt köşesi olsun.
  • Soru, C ile L arası mesafe |CL| kaç cm?

Çözüm

  1. Dikdörtgenin yüksekliği (OA)=2 cm.
  2. Yarıçap R=3 cm ise, merkezin üst kenara dik uzaklığı 2 cm olduğundan, oradaki kirişin yarı uzunluğu \sqrt{3^2 - 2^2} = \sqrt{9 - 4} = \sqrt{5} olur. Bu, yarım çember üzerindeki kirişin yarısıdır.
  3. Dikdörtgen tam ortalandıysa, alt kenar (OC) da benzer projeksiyonla yanal uzunluk verebilir.
  4. C noktası yarım çemberin alt kenarına oturuyorsa, |CL| = ? Bulmak için “tüm çap” – “BC veya benzeri” yaklaşım olur.

Bu tip bir örnekten görüldüğü gibi, her problemde sayılar değişse de mantık aynıdır:

  • Kiriş–merkez uzaklığı ilişkisi
  • Dikdörtgenin kenarları
  • Çemberin çapından artan mesafe

Gerçek sorunuzda R kaç, A noktası çemberin neresinde gibi soruları netleştirerek benzer bir yol izlenmelidir.

—

7. Sık Yapılan Hatalar ve İpuçları

  1. Yanlış Noktayı R Sanmak: Bazen “OA=2 cm” ifadesi direk R=2 cm anlamına gelmeye bilir. Nokta A çember üzerinde değilse, R=2 cm hatalı olur.
  2. Kenar Adlandırmada Karışıklık: Şekildeki harfleri doğru eşleştirmemek, mesafeleri yanlış hesaplamaya yol açar.
  3. Pisagor Yerine Yanlış Teorem Kullanmak: Dik açı olmayan veya doğru parça olmayan yerlerde hatalı uygulama yapmak.
  4. Uzunluk Birimlerini Karıştırmak: cm yerine m, ya da rakamsal hatalar.

İpuçları:

  • Şekil çiziminde merkez, yarıçap, dik kenar ayrıntılarını renkli kalemle vurgulayın.
  • Gerekirse koordinat sistemi kurarak O noktasını orijin (0,0) kabul edip, yarıçapı R olarak alabilirsiniz. Noktalar bu koordinatta (x,y) şeklinde tanımlanarak, (x^2 + y^2 = R^2) çember denkleminden faydalanılabilir.

—

8. Özet Tablo

Aşağıdaki tabloda, yarım çember ve dikdörtgen ilişkilerine dair genel çözüm adımlarını özetliyoruz:

Adım İşlem Not
1. Nokta Tanımları ve Veriler Şekilde merkez (O), yarıçap (R), çap uçları (K ve L), dikdörtgen köşeleri (A,B,C vb.) netleştirilir. Yanlış noktayı çember üzerinde varsaymamaya dikkat edin.
2. Verilenlerin Gösterimi OA
3. Temel Formülü Seçme - Pisagor Teoremi: a^2 + b^2 = c^2
- Kiriş ve merkez uzaklığı: kiriş\_yarısı = \sqrt{R^2 - d^2}		 Hangi teorem veya ilişki uygunsa onu seçin.
4. Denklemleri Oluşturma Elde ettiğiniz geometrik ifade ve teoremleri birleştirerek denklemlerinizi yazın. Özellikle çemberin yarıçapı, dikdörtgen (ya da üçgen) kenarları ve aradığınız x arasındaki ilişkiyi formülleştirin.
5. Denklemi Çözme Denklemleri düzenleyip x, R, vb. bilinmeyeni hesaplayın. Çözüm sonrası boyutların fiziki mantığını kontrol edin (örneğin x, R’den büyük olmamalı vs.)
6. Mantık Kontrolü ve Sonuç Bulduğunuz değeri şekle geri dönerek test edin. Boyutlar, çember yarıçapı ve sorunun metnine uygun mu, bakın.

—

9. Sonuç ve Genel Özet

  • Sorunuzun kilit noktası: Yarım çember üzerinde veya içerisinde bir dikdörtgen var ve bir kenarın (örneğin |OA|) 2 cm olarak verildiği belirtiliyor. İstenen |CL| gibi bir kenar uzunluğu veya kiriş/bölüm uzunluğu, tipik olarak Pisagor Teoremi ya da kiriş-uzaklık ilişkisiyle bulunur.
  • Mutlaka şekli net şekilde adlandırın: Hangi noktalar çember üstünde, hangisi çap üstünde, hangi uzunluk yarıçap?
  • Dikdörtgenin köşeleri çemberin yayına oturuyorsa, oradaki kenar(lar) çember denklemini sağlamalı. Bu da “$x^2 + y^2 = R^2$” veya “$kiriş = 2 \sqrt{R^2 - d^2}$” gibi formüllerle ifade edilir.
  • Sonuçta “x = ?” gibi sorularda elde ettiğiniz ifadenin, problem verileri ile tutarlı olduğuna özen gösterin.

Eğer problem tam olarak şunu diyorsa:

  1. O merkezli, KL çaplı bir yarım çember var.
  2. Bir dikdörtgen ABOC içindeyiz.
  3. |OA| = 2 cm.
  4. |CL| = x’in değeri nedir?

Ve eğer A yarım çemberin tepe noktasında (yani A çember üzerinde) ise, yarıçap muhtemelen 2 cm’dir. Bu durumda KL=4 cm olur. O hâlde C noktası çap üstünde başka bir nokta ise |CL|, 4 cm içindeki bir parça olabilir. Çeşitli benzer üçgen ilişkileri devreye girecektir.

Öte yandan, definitif bir cevap için net şekil analizine ihtiyaç var. Yukarıdaki yöntemle, şekli adım adım tarifleyip, hangi uzunluğun nasıl elde edileceğini rahatça bulabilirsiniz.

@Ruveyda_Kirmizioglan